算法学习（持续更新中）

时间复杂度

一个操作如果和样本的数据量没有关系，每次都是固定时间内完成的操作，叫做常数操作。

时间复杂度为一个算法流程中，常数操作数量的一个指标。常用O（读作big O）来表示。具体来说，先要对一个算法流程非常熟悉，然后去写出这个算法流程中发生了多少常数操作，进而总结出常数操作数量的表达式。

在表达式中，只要高阶项，不要低阶项，也不要高阶项的系数，剩下的部分如果为f(N)，那么时间复杂度就位O(f(N))。

评价一个算法流程的好坏，先看时间复杂度的指标，然后再分析不同数据样本下的实际运行时间，也就是“常数项时间”.

常数操作：例如数组根据索引寻值，加、减、乘、除、比较

排序

选择排序

每次选择 i 到 n-1 范围内值最小的索引位置 t ，每一次内层循环结束之后交换 i 和 t 索引位置上的值，每一次外层循环 i 的值加 1

private static void selectSort(Integer[] nums) {for(int i=0;i<nums.length-1;i++){int t=i;for(int j=i+1;j<nums.length;j++){if(nums[t]>nums[j]){t=j;}}swap(nums,i,t);}}

时间复杂度：O(n^2) ，空间复杂度：O(1)

冒泡排序

每次从 0 到 i 的范围中将相邻的值进行两两比较，将大的一个值移到后面，这样每一次内层循环结束后，i 位置的值就是0 到 i 范围内最大的值，每一次外层循环 i 的值减 1.

private static void BubbleSort(Integer[] nums) {int n=nums.length;for(int i=n-1;i>0;i--){for(int j=0;j<i;j++){if(nums[j]>nums[j+1]){swap(nums, j, j+1);}}}}

时间复杂度：O(n^2) ，空间复杂度：O(1)

插入排序

i 从 0 开始，维护一个 0 到 i 范围的有序数组，每一次 i++ ，令 j 等于 i，j 所在位置的元素和 j-1 所在位置的元素进行比较因为前 j-1 个元素是有序的，所以 j 就往前进行比较，如果 j 所在位置比 j-1 小,就进行交换，再往前进行比较，知道比前面的大为止。

private static void MySort(Integer[] nums) {if(nums==null || nums.length<2){return;}int l=nums.length;for(int i=1;i<l;i++){for(int j=i;j>0;j--){if(nums[j]<nums[j-1]){swap(nums,j,j-1);}else{break;}}}}

最坏情况下时间复杂度为 O(n^2)，空间复杂度为O(1)

异或运算

异或运算也叫做无进位运算，当两个操作数相同时，异或运算的结果为 0。当两个操作数不同时，异或运算的结果为 1。

1011 ^ 1001  = 0010  ， 0 ^ N = N  ,  N ^ N = 0
1 0 1 11 0 0 1=  0 0 1 0//异或操作满足交换律和结合率：a^b=b^aa^bc=a^(b^c)

当交换两个数的值时，可以使用异或操作，这样就不会产生额外的空间

    @Testpublic void swap(){int a=1;int b=2;
a=a^b;b=a^b;a=a^b;System.out.println("a="+a+"\n"+"b="+b);}


输出：a=2b=1

原因：

a=1,b=2
第一次异或： a=a^b,b=b   ---> a=1^2,b=1
第二次异或： a=a^b,b=a^b^b=a  ---> a=1^2,b=1^2^2-->因为2^2=0,所以b=1^0=1
第三次异或： a=a^b^a,b=a  ---> a=1^2^1(原本是a^b^b，因为后面一个b在第二步异或的时候变成了a的值，所以这里是1)-->a=1^1^2=0^2=2

所以a和b就完成了交换。

但是：使用异或操作完成的交换功能在程序中只能作用于地址位置不同的两个对象，如果是同一个地址位置来进行异或，会把值抹为0

例：存在一个int类型的数组

（1）其中有一种数出现了奇数次，其余都出现了偶数次，求这个奇数次的数 （使用时间复杂度为（O(n)，空间复杂度为O(1)）。

使用一个整数0，对数组中的每一个数进行异或运算，因为异或运算不在乎数的顺序，所以就是 0 ^ 所有的偶数次的数（为0）^ 奇数次的数(剩一个) ---> 结果就是 0 ^ 一个奇数次的数 = 奇数次的数。

//int[] nums=new int[]{0,0,1,3,1,2,3};
public static void printOddTimesNum1(int[] nums){int eor=0;for (int num : nums) {eor=eor^num;}System.out.println(eor);}

/**输出为：2
**/

（2）有两种数出现了奇数次，其余都出现了偶数次，求这个偶数次的数

//int[] nums=new int[]{0,1,3,1,2,3};
public static void printOddTimesNum2(int[] nums){int eor=0;/**eor = 奇数1 ^ 奇数2，因为奇数1和奇数2不相同，所以eor一定不等于0，这表示eor的32位二进制中至少有一位为1.那么在为1的这个二进制位置上，奇数1和奇数2的值一定不同（一定是其中一个为1，另一个为0），所以我们就可以先求出这个位              置，然后再去与数组中的值进行异或，得到其中一个奇数**/for (int num : nums) {eor=eor^num;}/**这里就是来求出最右边为1的位置例如：eor = 10100 ~eor = 01011  ~eor+1 = 01100eor & ~eor+1 :  1010001100--->   00100所以最右边为1的位置就是00100（4）**/int rightIndex=eor & ~eor+1;int onlyOne=0;for (int num : nums) {if((num & rightIndex)==1){//如果右边第4为为1才进行异或运算，onlyOne最后得到的就是奇数1或者奇数2的值onlyOne = onlyOne^num;}}System.out.println("num1:"+onlyOne+"\n"+"num2:"+(eor ^ onlyOne));}

//输出： num1:0
//      num2:2

二分查找

1）在一个有序数组中，找某个数是否存在

//int res=binarysearch(nums,target,0,nums.length-1);
private static int binarysearch(Integer[] nums, Integer target,Integer left,Integer right) {if(left>right) return -1;int l=left;int r=right;int mid=(l+r)>>>1;if(nums[mid]>target){return binarysearch(nums,target,left,mid-1);}else if(nums[mid]<target){return binarysearch(nums,target,mid+1,right);}
return mid;}

2）在一个有序数组中，找 >= 某个数最左侧的位置

/**Integer[] nums2={1,1,1,1,1,2,2,2,2,2,3,3,3,3,4,4,4,4,5,5,5};System.out.println(binarysearch2(nums2, 3, 0, nums2.length - 1));
**/
private static int binarysearch2(Integer[] nums, Integer target,Integer left,Integer right) {if(left>right) return -1;int l=left;int r=right;int t=0;while(l<=r){int mid=(l+r)>>>1;if(nums[mid]>=target){/*** 找到了一个 >= target的数，将位置记录下来，* 不过也可能在这个数的左边还存在 >= target 的数，* 所以就更新右边界,去左边继续寻找*/t=mid;r=mid-1;}else{//这里就是 nums[mid]的值比target要小，更新左边界，继续去数组右边去找l=mid+1;}}
return t;}

//输出：10

3）局部最小值问题 （数组无序，相邻的两个数不相等局部最小定义：arr[0] < arr[1] 数组0位置的值就是局部最小，arr[arr.length-1] < arr[arr.length-2] 数组最后一个位置的值就是局部最小，对于数组其他位置上的数，满足 arr[i-1] > arr[i] < arr[i+1] i位置上的数就是局部最小）

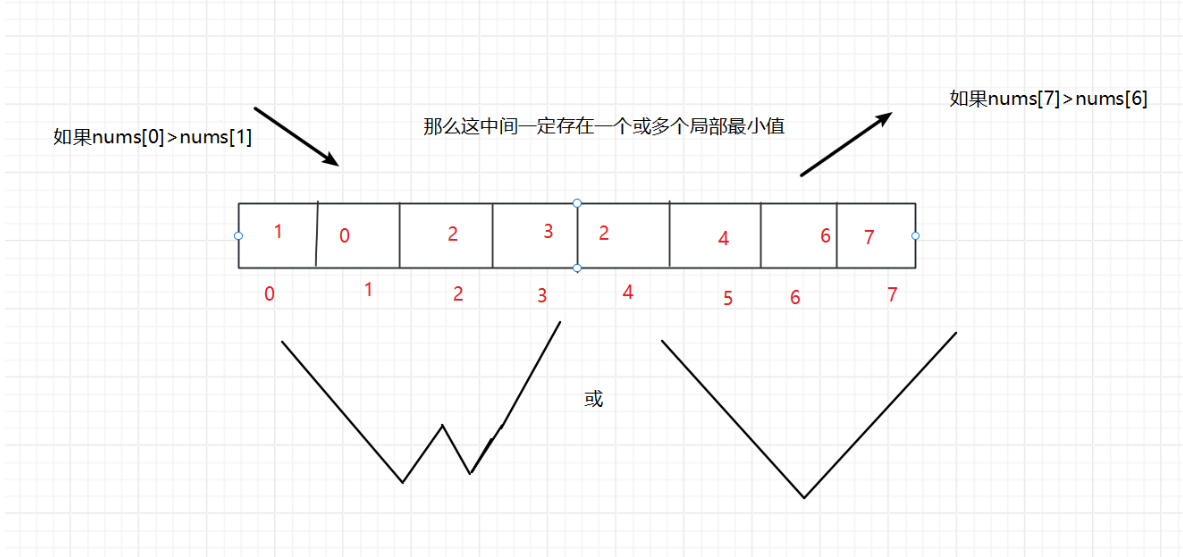
/**Integer[] nums3={1,0,1,3,6,5,1,2,3};System.out.println(binarysearch3(nums3));
**/
private static int binarysearch3(Integer[] nums) {int l=0;int r=nums.length-1;if(nums[l]<nums[l+1]) return l;if(nums[r]<nums[r-1]) return r;//如果执行到了这里，表示数组的两个边界都不是局部最小值，那么在这数组之中，一定存在一个局部最小值while(l<=r){int mid=(l+r)>>>1;if(nums[mid]<nums[mid-1] && nums[mid]<nums[mid]+1){return mid;}if(nums[mid]>nums[mid-1]){r=mid-1;} else if (nums[mid]>nums[mid+1]) {l=mid+1;}}return -1;}

//输出： 1

对数器

有一个你想要测的方法 a，

实现复杂度不好但是容易实现的方法 b ，

实现一个随机样本产生器，

把方法 a 和方法 b 跑相同的随机样本，看看得到的结果是否一样。

如果有一个随机样本是的对比结果不一致，打印样本进行人工干预，改对方法 a 或方法 b

当样本数量很多时对比测试是否依然正确，如果依然正确，就可以确定方法 a 已经正确

这里以插入排序作为方法a，java中本身提供的sort方法作为方法b

public static void main(String[] args) {int testTime=500000;int maxSize=100;int maxValue=100;boolean succeed=true;for(int i=0;i<testTime;i++){int[] arr1=generateRandomArray(maxSize,maxValue);int[] arr2=copyArray(arr1);//对arr1数组深拷贝MySort(arr1);//插入排序 a方法comparator(arr2);//b方法if(!isEqual(arr1,arr2)){//如果排序后的两个方法中的值存在差异succeed=false;break;}}System.out.println(succeed ? "Nice":"Fucking fucked");
int[] array = generateRandomArray(maxSize, maxValue);System.out.println(Arrays.toString(array));MySort(array);System.out.println(Arrays.toString(array));
}

//随机生成一个长度位maxSize，最大值为maxValue的int类型的数组public static int[] generateRandomArray(int maxSize,int maxValue){/*** Math.random() -> [0,1) 所有的小数，等概率返回一个 因为在计算机中，数的位数是有限制的，所以可以确定所有的小数，在数学上就不行。* Math.random()*N -> [0,N) 所有的小数，等概率返回一个* (int)(Math.random()*N) -> [0,N-1] 所有的整数，等概率返回一个*/
int[] arr=new int[(int)((maxSize+1)*Math.random())];//长度随机for(int i=0;i<arr.length;i++){arr[i]=(int) ((maxValue+1)*Math.random())-(int)(maxValue*Math.random());}return arr;}


//深拷贝
private static int[] copyArray(int[] arr1) {if(arr1==null) return null;int[] arr=new int[arr1.length];for (int i = 0; i < arr1.length; i++) {arr[i]=arr1[i];}return arr;}

//插入排序
private static void MySort(int[] nums) {if(nums==null || nums.length<2){return;}int l=nums.length;for(int i=1;i<l;i++){for(int j=i;j>0;j--){if(nums[j]<nums[j-1]){swap(nums,j,j-1);}else{break;}}}}

//交换
private static void swap(int[] nums, int i, int j) {int tmp= nums[i];nums[i]= nums[j];nums[j]=tmp;}

//java提供的方法
private static void comparator(int[] arr2) {Arrays.sort(arr2);}

//比较两个数组中的内容是否完全一致
public static boolean isEqual(int[] arr1,int[] arr2){for (int i = 0; i < arr1.length; i++) {if(arr1[i]!=arr2[i]) return false;}return true;}