1.线性方程组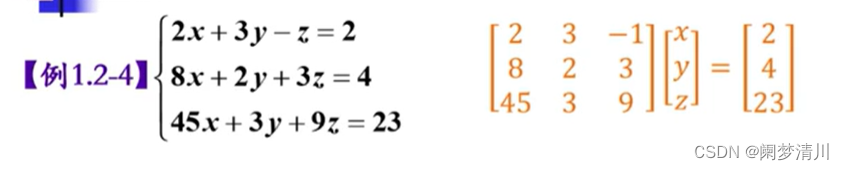


这个是一个线性方程组(属于线性代数的范畴),Ax=b类型的方程,如果使用MATLAB进行求解,就需要分别表示A矩阵(线性方程组未知数前面的系数),b矩阵(表示等式右边的结果),inv是这个软件里面的一个函数,用来进行求解A的逆矩阵,因为Ax=b,那么x=A-1次方乘上b

另外,我们也可以使用这个A\b来进行求解,这个里面需要注意是A\b,而不是我们熟悉的A/b,他们所代表的含义是不一样的,我们在脚本里面敲代码的时候,需要在前面的2行加上结尾处的引号,最后一行不用加引号,否则我们在命令行窗口里面无法看到最后的输出结果;
2.二维图形的绘制
二维图形的绘制要是用这个plot函数,我们通过这个例子来认识一下函数的使用方法,以sin1/x为例吧:

(1)这个地方我们只绘制了-1~1范围里面的函数图像,这样便于观察函数的效果,学过高等数学的同学们对于这个函数就非常的熟悉,因为他是特例,这个函数是有界限的,但没有极限存在;
(2)下面我们来聊一聊这个里面每一行代码的作用,首先,第一行是生成行向量,我们可以简单地理解为,通过这一行,我们要告诉MATLAB我们要绘制图像的定义域是-1~1之间的,100000是在这个-1~1这个区间里面生成100000个采样点,
(3)这个里面使用了点运算符,只要是涉及到矩阵里面的元素运算,我们在大部分的情况下都要是用这个运算符,后续还会涉及到,这个运算符在矩阵的运算里面很常见,我们都知道,对于两个矩阵的乘法运算,他们并不是对应位置的元素相乘,但是如果我们使用点乘运算符,就可以让矩阵里面对应位置的元素进行相乘的运算;
**************************************************************************************************************
接下来我们举一个在一个坐标平面里面绘制2个图形的例子
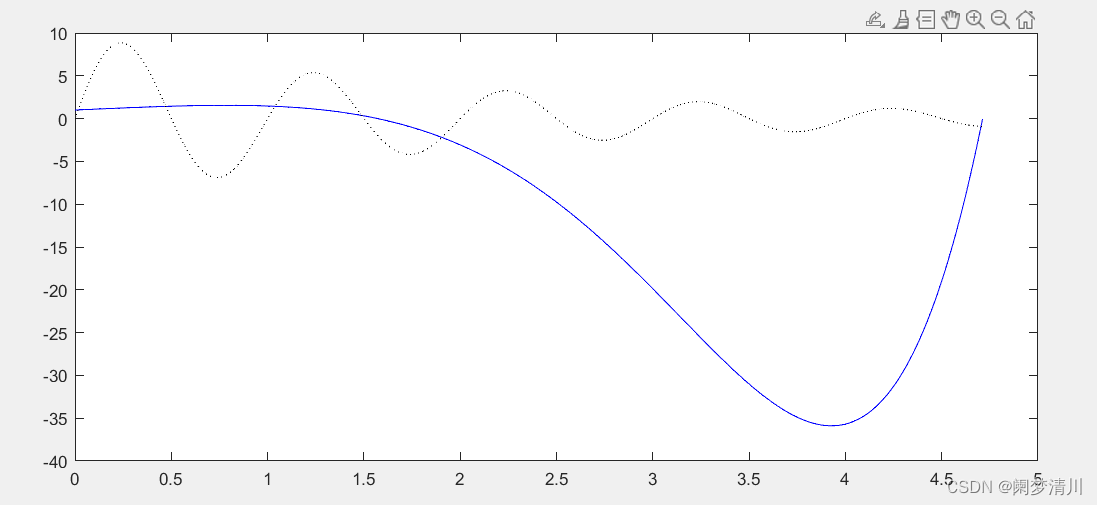
我们在一个坐标平面里面绘制y=e^x*cos和y=10*e^-0.5x*sin(2pi x)的函数图像(0~pi/2区间里面)

这个里面的plot中的单引号里面表示的是一些标记符号;
b是蓝色,-表示实线;合在一起就是蓝色实线;
k表示黑色,:表示虚线;合在一起就是黑色虚线;
下面是效果图:
3.空间曲线的绘制
绘制空间曲线x^2+y^2+z^2=16,x+y=0(这2个方程是在一个括号里面进行联立的)
首先要转化成为参数方程,也就是x=2根号2sint;y=-2根号2cost;z=4cost;

下面是是否添加grid on的区别,读者可以自行感受:

这个是没有grid on的,可见就没有曲线的格子;
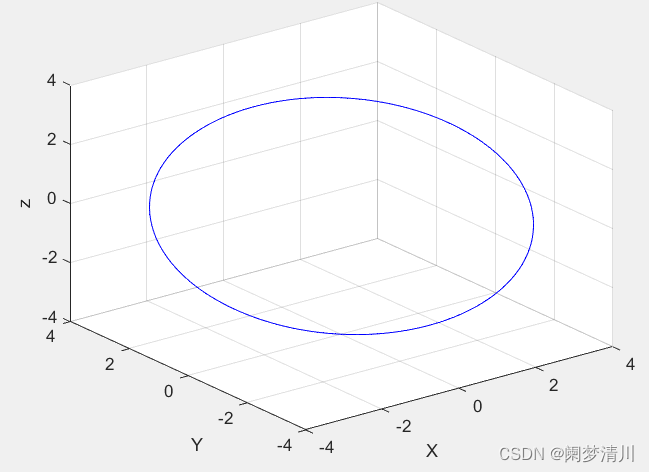
这个是添加了grid on的,差别就显而易见了;
4.函数极限实验
(1)符号运算,matlab使用sym创建符号对象,一次只能够创建一个符号对象,我们也可以使用syms一次性创建多个符号对象;
(2)极限运算
MATLAB提供limit函数求极限
limit(f,x,a)表示求f(x)在a点处的极限值;
limit(f,x,a,'right')是求这点处的右极限,如果我们把right换成left就是求左极限;
当然,也可以进行求解多元函数的极限:这个时候就需要嵌套limit;
z=limit(limit(f,x,x0),y,y0)就是求在x0,y0处的极限值;

f1里面就是我们要求的函数的表达式,在x趋近于1的极限值;
![]()
我们都知道sin(1/x)的极限是不存在的,所以程序的输出结果就是NaN;
5.MATLAB求导运算
MATLAB里面可以调用diff函数求函数的导函数;
例如diff(f,x,5)就是求符号函数f在x这个点处的5阶导数;
接下来我们使用MATLAB求一下y=x^2*exp(-x)的3阶导数;

6.MATLAB实现函数的泰勒幂级数展开

taylor里面就是我们要展开的函数表达式;
6.MATLAB积分实验
我们使用int(s,x)就是表示对s表达式里面的x进行积分;
顺便提一句:无论是积分求解还是极限的求解,我们都是使用inf代表无穷;
下面是例子:
(需要了解的是这个不定积分的求解是没有常数项的(实际上数学里面的求解是由常数的))

当然,MATLAB也是可以计算定积分的:
对于积分的上下限,我们在int(s,x,a,b)里面添加2个参数,a是积分下限,b是积分的上限

7.MATLAB实现微分方程
Dny表示y的n阶导,D2y就是2阶导;我们可以调用dsolve函数实现常微分方程的求解;
这个板块不同的版本软件的代码语言有所差别,这个是以我的2023为例
(1)我们去求dy/dx+y/x=sinx/x的通解:
diff就是求导数的运算;

(2)求解dy/dx+y=y^2*exp(-x)满足条件y(0)=-2的特解:
提前说明一下,笔者使用的是旧版本的教材,但是用的是新版MATLAB,2023里面可能会因为不支持原来的某些符号而报警告,但是我们依然是能够得到结果的;

D2y表示的是2阶导,D3y表示的是3阶导,以此类推;
(3)y''-6y'+13y=0的通解;

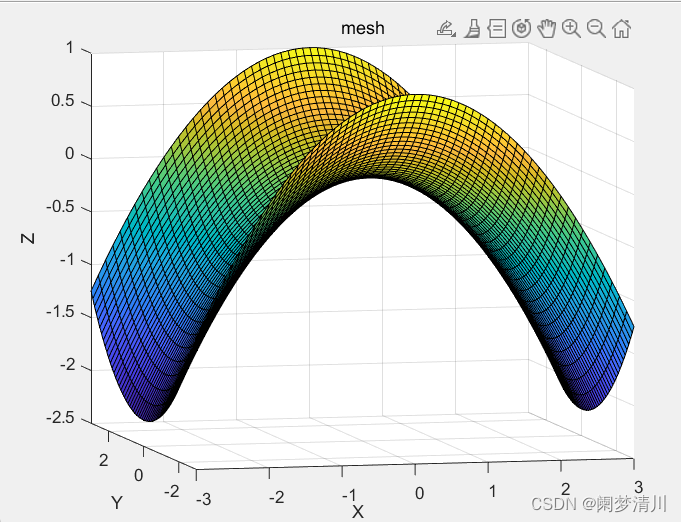
8.空间曲面(马鞍面&&双曲抛物面)


(1)同样是马鞍面,也叫做双曲抛物面,我们可以使用不同的函数进行绘制,不同的函数的展示的效果是不一样的,我们上面的是使用mesh函数绘制,这个函数主要是连接成网格点,下面的这个有颜色的马鞍面是用这个surf进行绘制的,代码的其他部分不变,只需要把第4行的函数的名字改变一下就可以了,通过这个案例我们也可以发现这两者之间的差别,前者线条有颜色,线条之间的补面没有颜色的填充,后者的曲面图线条是黑色的,之间使用颜色进行了填充;
(2)MATLAB为我们提供了grid函数决定是否显示分格线,他的调用格式为
grid od:显示分格子线
grid off:不显示分格子线
(3)相信你一定注意到了这个里面的点运算,点运算是MATLAB里面很有特色的一种运算,我们都知道,矩阵在进行乘法操作的时候,并不是对应的元素进行相乘,但是如果我们对于矩阵里面的元素使用点乘运算,就可以实现对应位置的元素相乘,在绘图里面这个运算有十分广泛的运用;
(4)这个里面的meshgrid也是一个函数,这个函数的功能就是生成网格数据,当X轴和Y轴的数据点个数相等的时候,我们就可以使用[x,y]=meshgrid(x,y);







)











