数据结构之优先级队列(堆) (PriorityQueue)

🎉欢迎大家观看AUGENSTERN_dc的文章(o゜▽゜)o☆✨✨

🎉感谢各位读者在百忙之中抽出时间来垂阅我的文章，我会尽我所能向的大家分享我的知识和经验📖

🎉希望我们在一篇篇的文章中能够共同进步！！！

🌈个人主页：AUGENSTERN_dc

🔥个人专栏：C语言 | Java | 数据结构

⭐个人格言：

一重山有一重山的错落，我有我的平仄

一笔锋有一笔锋的着墨，我有我的舍得

1.概念：

2. 堆的分类：

2.1 大根堆：

2.2 小根堆：

3. 堆的创建：

3.1 堆类的构建：

3.2 双亲节点和孩子节点的关系：

3.3 堆的初创建：

3.4 向下调整：

3.5 向上调整：

4. 优先级队列的模拟实现：

5. 优先级队列的模拟实现整体源码：

1.概念：

在我们之前的队列的文章中介绍过，队列是一种先进先出的数据结构，但有些情况下，操作的数据可能带有优先级，一般出队列时，可能需要优先级高的元素先出队列，该中场景下，使用队列显然不合适，比如：在手机上玩游戏的时候，如果有来电，那么系统应该优先处理打进来的电话；初中那会班主任排座位时可能会让成绩好的同学先挑座位。

如果我们给每个元素都分配一个数字来标记其优先级，不妨设较小的数字具有较高的优先级，（在后续中我们会讲到，这是小根堆）这样我们就可以在一个集合中访问优先级最高的元素并对其进行查找和删除操作了。这样，我们就引入了优先级队列这种数据结构。优先级队列（priority queue）是0个或多个元素的集合，每个元素都有一个优先权，对优先级队列执行的操作有

（1）查找

（2）插入一个新元素

（3）删除

一般情况下，查找操作用来搜索优先权最大的元素，删除操作用来删除该元素 。对于优先权相同的元素，可按先进先出次序处理或按任意优先权进行。

在jdk1.8中，PriorityQueue的底层是用堆这一数据结构实现的；

2. 堆的分类：

堆在逻辑上是一颗完全二叉树，但是堆的实现却是由数组实现的，我们是将这颗完全二叉树按照层序遍历的方式存放在数组中的；

堆分为两种：

2.1 大根堆：

大根堆是指根节点的值最大，左右子节点的值都小于根节点的完全二叉树按照层序遍历的方式存放到数组中的一个堆结构；

要想真正的了解堆这个结构，我们不妨从绘图开始理解：

首先我们试着画一个完全二叉树：

将上图的完全二叉树按照层序遍历的方式存放在数组中，如上图，就是一个大根堆；

我们会发现，在上图中的完全二叉树中，根节点25 的值是最大的，根节点25的左右节点的值都比25要小，同时，我们会发现，20节点和17节点的左右节点的值同样小于根节点的值；

这就是大根堆的特性；

2.2 小根堆：

小根堆和大根堆则相反，根节点的值要小于左右节点的值；

如下图

3. 堆的创建：

（！！！在接下来的内容中，所有的堆都以小根堆的形式创建！！！）

3.1 堆类的构建：

public class my_PriorityQueue {public int[] elem;              //堆的底层是数组实现的；public int usedSize;            //数组的使用长度private static final int DEFAULT_INITIAL_CAPACITY = 11;     //数组的默认长度public my_PriorityQueue() {//不带参数的构造方法}
}

3.2 双亲节点和孩子节点的关系：

如果堆的存储结构也是一颗完全二叉树的话，想要从根节点找到左右子树是很简单的事情，但是堆的存储结构是一个数组，那么我们又要如何才能找到他的左右子树呢？

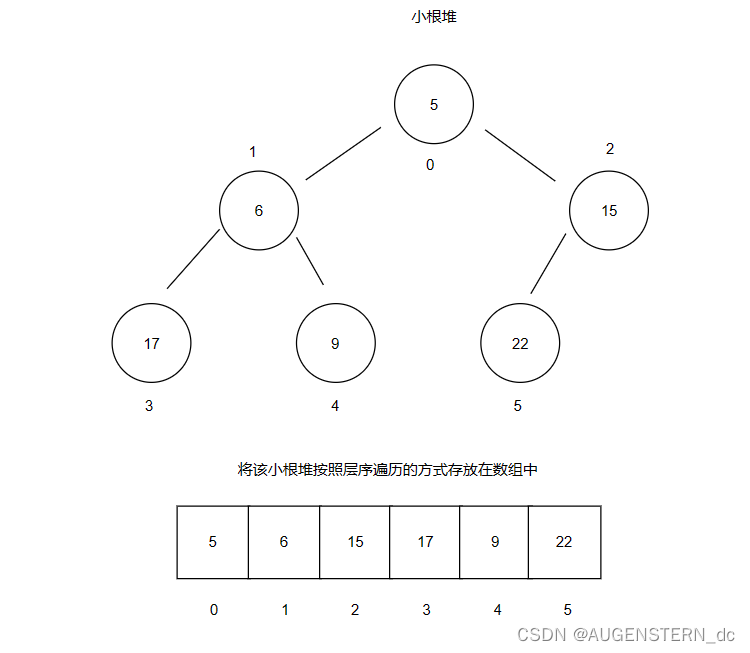
以上图的小根堆为例：

由于堆的底层是由数组实现的，那么每一个节点都会有一个对应的下标，我们将其标明在图上；

下标为0的节点的左右子树为1 和 2；下标为1的节点的左右子树的节点的下标为3 和 4；

假设双亲节点为 parent，孩子节点为 child，我们不难发现parent 和 child的关系：

（child - 1）/ 2 = parent

这就是双亲节点和孩子节点的关系；

有了这个关系，我们就可以开始试着创建堆了；

3.3 堆的初创建：

假如我们有一个空的小根堆，我们开始向空堆中插入元素，我们先插入值为4 的元素；

接下来为了保持小根堆这个结构，在插入元素之后，我们就需要开始考虑了；

首先我们将元素直接插在4的后面；

如果我们插入的值比插入节点的双亲节点（也就是4节点）大，我们应该保持插入元素的位置不变，

但是如果我们插入的元素比4小呢？我们就应该将该节点和4节点交换位置；

如图：

那是不是，每次我们插入元素的时候，我们需要进行比较和判断；

看插入的元素的大小和其双亲节点的大小相较之下如何；

但是，随着元素的增多：

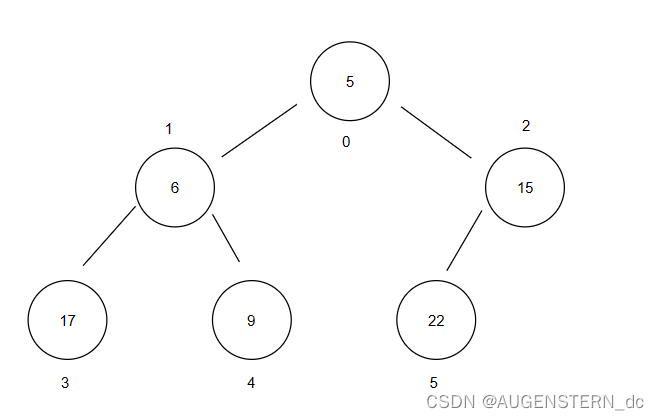
如果我们插入一个值为2的节点，我们发现，我们不仅需要2和15进行狡猾，并且交换玩之后，我们需要将2和5再次进行交换，这就会影响整棵完全二叉树；

同时我们会发现，我们有两种调整的方法，我们称为向下调整和向上调整：

在创建堆的时候我们一般使用向下调整：

我们用createHeap表示创建小根堆方法， shiftDown表示向下调整方法；

public void createHeap() {elem = new int[DEFAULT_INITIAL_CAPACITY];       //构造一个空的，大小为默认大小的堆}public void createHeap(int[] array) {               //构造一个元素和array数组相同的array小根堆elem = array.clone();usedSize = array.length;int child = array.length - 1;                   //孩子节点的下标int parent = (child - 1) / 2;                   //双亲节点的下标while (parent >= 0) {                           //从最后一个孩子节点的双亲节点一直向下调整到下标为0的节点shiftDown(parent, usedSize - 1);        //向下调整parent--;                           }}

3.4 向下调整：

以上图为例：向下调整就是从最后一个元素的双亲节点开始，依次和子节点比较大小，若需要互换，则进行调整，直到双亲节点的下标为0为止；

如图，就是依次将值为5的节点和值为22的节点，值为15的节点中的最大值比较，若需要交换则进行调整，一直从值为5的节点调整到值为2的节点为止；

向下调整一般在创建堆的时候进行使用：

接下来我们开始对小根堆的创建：

首先我们先随意给定一个整形数组，将其按照完全二叉树的逻辑排列

最后一个节点下标为5；那么其双亲节点为（ 5 - 1）/ 2 = 2；

随后我们需要判断下标为2的节点和下标为5的节点的大小，一直从下标为2的节点判断到下标为0的节点为止；

代码的思路大概构建出来了，我们开始着手写向下调整的代码：

private void swap(int x, int y) {int tmp = elem[x];elem[x] = elem[y];elem[y] = tmp;}

private void shiftDown(int root,int len) {int parent = root;int child = parent * 2 + 1;while (child <= len) {                                              //若有两个孩子节点child = elem[child] < elem[child + 1] ? child : child + 1;      //找出两个孩子节点中的最大的节点if (elem[parent] > elem[child]) {                               //若孩子节点大于双亲节点swap(child, parent);                                        //交换孩子节点和双亲节点parent = child;                                             //将parent重置为childchild = parent * 2;                                         //重置child，判断交换后的子树是否需要调整} else {break;                                                      //若无需调整，则直接跳出循环}}}

3.5 向上调整：

向上调整一般在插入元素的时候使用，例如在已经创建完成的堆中插入一个元素，一般是先将该元素放在数组的最后，然后依次将其和双亲节点进行大小比较，直到孩子节点的下标为0或者不需要和双亲节点进行交换为止，如图所示：

在这样一个小根堆中，我们插入一个元素3

此时的child = 7，parent = 3，首先我们来判断3和17 的大小，很明显，需要交换：

交换完成之后，我们将child = parent = 3，此时的parent = 1；

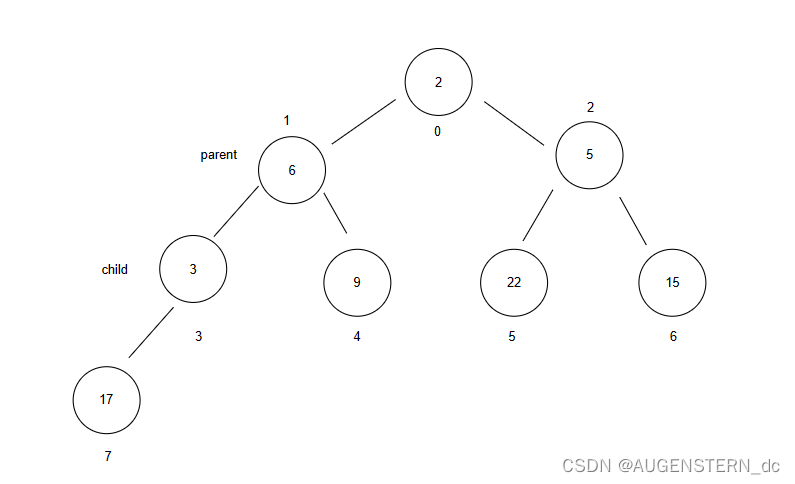
此时我们继续判断child和parent 的大小关系，还是需要交换3 和 6，再将child = parent，

parent = （child + 1）* 2 = 0；

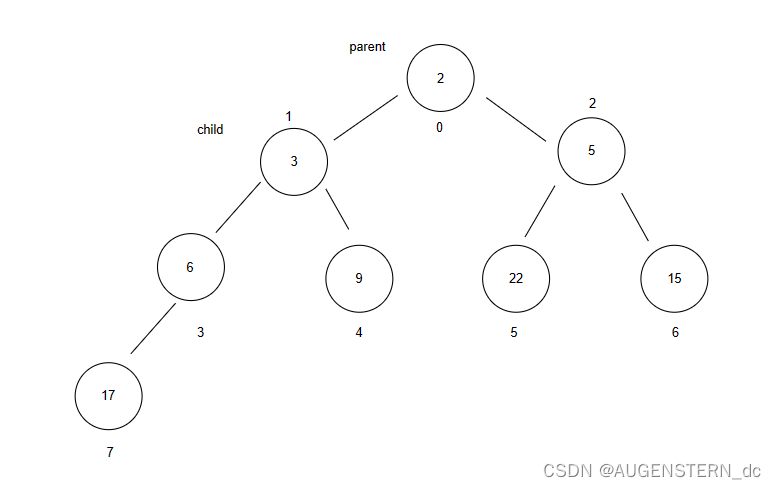
继续比较child和parent的值的大小关系，发现并不需要比较了，那我们就停止判断即可；

这就是向上调整的思路：

private void shiftUp(int child) {int parent = (child - 1) / 2;while (parent >= 0 && child != 0) {if (elem[child] < elem[parent]) {       swap(child, parent);child = parent;parent = (child - 1) / 2;} else  {break;}}}

4. 优先级队列的模拟实现：

Java集合框架中提供了PriorityQueue和PriorityBlockingQueue两种类型的优先级队列，PriorityQueue是线程不安全的，PriorityBlockingQueue是线程安全的，本文主要介绍PriorityQueue。

和队列的模拟实现类似，优先级队列同样有插入元素，删除元素和获得队头元素的方法：

< 1 > 插入元素：

每次插入元素之前，我们需要判断堆是否满了，若满了，则进行扩容：

private void grow() {int len = elem.length;if (len < 64) {elem = Arrays.copyOf(elem, DEFAULT_INITIAL_CAPACITY * 2);} else {elem = Arrays.copyOf(elem, DEFAULT_INITIAL_CAPACITY + DEFAULT_INITIAL_CAPACITY >> 1);}}

判断完成后，我们需要将插入元素后的新堆调整为大根堆或者小根堆，我们这里以小根堆为例：

public void offer(int val) {if (isFull()) {grow();}if (usedSize == 0) {elem[0] = val;usedSize++;return;}elem[usedSize] = val;shiftUp(usedSize);usedSize++;}

< 2 > 删除元素：

由于删除元素是将堆顶元素进行删除，我们可以先将堆顶元素和堆末尾的元素进行交换，将堆末尾的元素删除也就是将usedsize - - 即可；

public void pollHeap() {swap(0, usedSize - 1);usedSize--;shiftDown(0, usedSize - 1);}

< 3 > 获得队头元素：

public int peekHeap() {return elem[0];}

还有size() , isEmpty() ,clear()方法，由于太简单，这里就没有写了；

5. 优先级队列的模拟实现整体源码：

import java.util.Arrays;public class my_PriorityQueue {public int[] elem;              //堆的底层是数组实现的；public int usedSize;            //数组的使用长度private static final int DEFAULT_INITIAL_CAPACITY = 11;     //数组的默认长度public my_PriorityQueue() {//不带参数的构造方法}/*** 建堆的时间复杂度：** @param array*/public void createHeap() {elem = new int[DEFAULT_INITIAL_CAPACITY];       //构造一个空的，大小为默认大小的堆}public void createHeap(int[] array) {               //构造一个元素和array数组相同的array小根堆elem = array.clone();usedSize = array.length;int child = array.length - 1;                   //孩子节点的下标int parent = (child - 1) / 2;                   //双亲节点的下标while (parent >= 0) {                           //从最后一个孩子节点的双亲节点一直向下调整到下标为0的节点shiftDown(parent, usedSize - 1);        //向下调整parent--;}}/**** @param root 是每棵子树的根节点的下标* @param len  是每棵子树调整结束的结束条件* 向下调整的时间复杂度：O(logn)*/private void shiftDown(int root,int len) {int parent = root;int child = parent * 2 + 1;while (child <= len) {                                              //若有两个孩子节点child = elem[child] < elem[child + 1] ? child : child + 1;      //找出两个孩子节点中的最大的节点if (elem[parent] > elem[child]) {                               //若孩子节点大于双亲节点swap(child, parent);                                        //交换孩子节点和双亲节点parent = child;                                             //将parent重置为childchild = parent * 2;                                         //重置child，判断交换后的子树是否需要调整} else {break;                                                      //若无需调整，则直接跳出循环}}}/*** 入队：仍然要保持是小根堆* @param val*/public void offer(int val) {if (isFull()) {grow();}if (usedSize == 0) {elem[0] = val;usedSize++;return;}elem[usedSize] = val;shiftUp(usedSize);usedSize++;}private void shiftUp(int child) {int parent = (child - 1) / 2;while (parent >= 0 && child != 0) {if (elem[child] < elem[parent]) {swap(child, parent);child = parent;parent = (child - 1) / 2;} else  {break;}}}private void swap(int x, int y) {int tmp = elem[x];elem[x] = elem[y];elem[y] = tmp;}public boolean isFull() {return usedSize == elem.length;}private void grow() {int len = elem.length;if (len < 64) {elem = Arrays.copyOf(elem, DEFAULT_INITIAL_CAPACITY * 2);} else {elem = Arrays.copyOf(elem, DEFAULT_INITIAL_CAPACITY + DEFAULT_INITIAL_CAPACITY >> 1);}}/*** 出队【删除】：每次删除的都是优先级高的元素* 仍然要保持是大根堆*/public void pollHeap() {swap(0, usedSize - 1);usedSize--;shiftDown(0, usedSize - 1);}public boolean isEmpty() {return usedSize == 0;}/*** 获取堆顶元素* @return*/public int peekHeap() {return elem[0];}
}

以上就是优先级队列的全部内容了，感谢大家的收看，谢谢！！！！

如果觉得文章不错的话，麻烦大家三连支持以下ಠ_ಠ