Day 51

01. 单词拆分（No. 139）

题目链接

代码随想录题解

<1> 题目

给你一个字符串 s 和一个字符串列表 wordDict 作为字典。如果可以利用字典中出现的一个或多个单词拼接出 s 则返回 true。

**注意：**不要求字典中出现的单词全部都使用，并且字典中的单词可以重复使用。

示例 1：

输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以由 “leet” 和 “code” 拼接成。

示例 2：

输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解释: 返回 true 因为 “applepenapple” 可以由 “apple” “pen” “apple” 拼接成。
注意，你可以重复使用字典中的单词。

示例 3：

输入: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出: false

<2> 笔记

给定一个字符串，问这个字符串能不能拆分成字典中的元素；反过来看就是字典中的字符串能不能填满这个字符串。而且字典中的字符是可以 无限次 使用的，这其实就类似一个 完全 背包问题；构建一个 01背包问题和构建一个完全背包问题的递推公式的最大区别其实就是，能不能在取得这个物品的状态的基础上再次取得物品。

先来看题目中有什么状态，以及这个状态能否被转移：题目中问的是能否利用字典中的内容来构成这个字符串，对于一个字符串，划分其状态最好的方式其实就是其 长度，如果知道其中的 一段 是可以由字典中的内容来组成的，那这个状态能否可以转移呢？

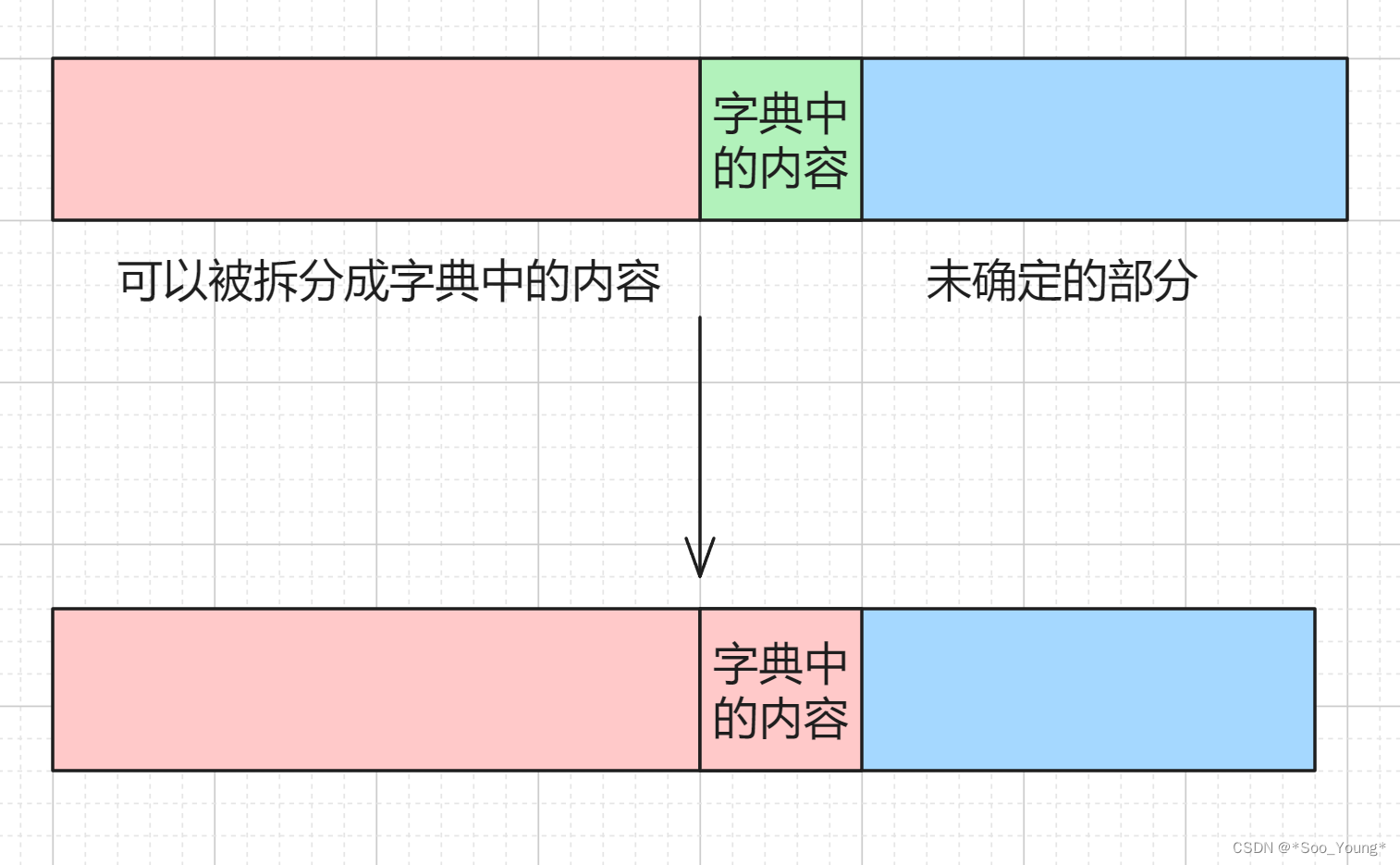
如果这个遍历到的部分前面是可以拆分成字典中的内容，并且 这样一段中还是字典中的内容的话，那这一段加上前一段就是可以被拆分成字典中的内容了，这样状态就得到了转移。

那这样 dp 数组的含义也确定了，即从 index = 0 到 index = i 能否拆分成字典中的单词。

再来考虑初始化，毫无疑问 dp[0] 是要初始化为 true 的，否则遍历是没有意义的。

首先来遍历字符串的长度

for (int i = 0; i < dp.length; i++) {}

再去确定 dp[i] 是否符合要求，这时候需要一个变量从头开始遍历，来检测某一段是否为 true

for (int j = 0; j < i && !dp[i]; j++) {if (dp[j]) {}
}

但这样是不够的，还需要从 j 到 i 的这一段也是字典中的单词，即要添上另一个条件：

if (dp[j] && wordDict.contains(s.substring(j, i))) {dp[i] = true;
}

这样其实就写出了递推公式。

<3> 代码

class Solution {public boolean wordBreak(String s, List<String> wordDict) {boolean[] dp = new boolean[s.length() + 1];dp[0] = true;for (int i = 1; i < dp.length; i++) {for (int j = 0; j < i && !dp[i]; j++) {if (dp[j] && wordDict.contains(s.substring(j, i))) {dp[i] = true;}}}return dp[s.length()];}
}

02. 多重背包理论基础

2.1 解题思路

与01背包和完全背包不同的是，多重背包会规定每个物品 各有多少个，而不是简单的一个或者无数个。

但是解决多重背包问题的思路也很简单，我只需要将这每个物品 看成多个重量和价值都相同的物品即可，这样就可以通过处理01背包的思路来决解决这个问题了，但这种解法是最优的嘛？这里先按下不表，先来看一个例题。

2.2 携带矿石资源（卡码网No.56）

<1> 题目

题目链接

代码随想录题解

题目描述

你是一名宇航员，即将前往一个遥远的行星。在这个行星上，有许多不同类型的矿石资源，每种矿石都有不同的重要性和价值。你需要选择哪些矿石带回地球，但你的宇航舱有一定的容量限制。

给定一个宇航舱，最大容量为 C。现在有 N 种不同类型的矿石，每种矿石有一个重量 w[i]，一个价值 v[i]，以及最多 k[i] 个可用。不同类型的矿石在地球上的市场价值不同。你需要计算如何在不超过宇航舱容量的情况下，最大化你所能获取的总价值。

输入描述

输入共包括四行，第一行包含两个整数 C 和 N，分别表示宇航舱的容量和矿石的种类数量。
接下来的三行，每行包含 N 个正整数。具体如下：
第二行包含 N 个整数，表示 N 种矿石的重量。
第三行包含 N 个整数，表示 N 种矿石的价格。
第四行包含 N 个整数，表示 N 种矿石的可用数量上限。

输出描述

输出一个整数，代表获取的最大价值。

输入示例

10 3
1 3 4
15 20 30
2 3 2

输出示例

90

提示信息
数据范围：
1 <= C <= 10000;
1 <= N <= 10000;
1 <= w[i], v[i], k[i] <= 10000;

<2> 笔记

和上面说的一样，本题是一个多重背包问题，题目输入中可以形成三个数组，首先是和前面相同的 weight 和 value 数组，还有每个物品的个数，number 数组。

首先想到的解题思路就是把所有重复的物品都当作单独的物品去处理，即第 i 个物品要遍历 number[i] 次，这才算遍历完了本次的物品，一共有 weight.length 个物品，每个物品有 number[i] 个，又要内层遍历背包，所以一共需要三层 for 循环，写出代码是这样的：

for (int i = 0; i < N; i++) { // 遍历矿石for (int j = 1; j <= number[i]; j++) { // 遍历矿石的数量for (int k = dp.length - 1; k >= weight[i]; k--) { // 遍历背包dp[k] = Math.max(dp[k], dp[k - weight[i]] + value[i]);}  }
}

---

但是提交之后会发现超时（大悲）

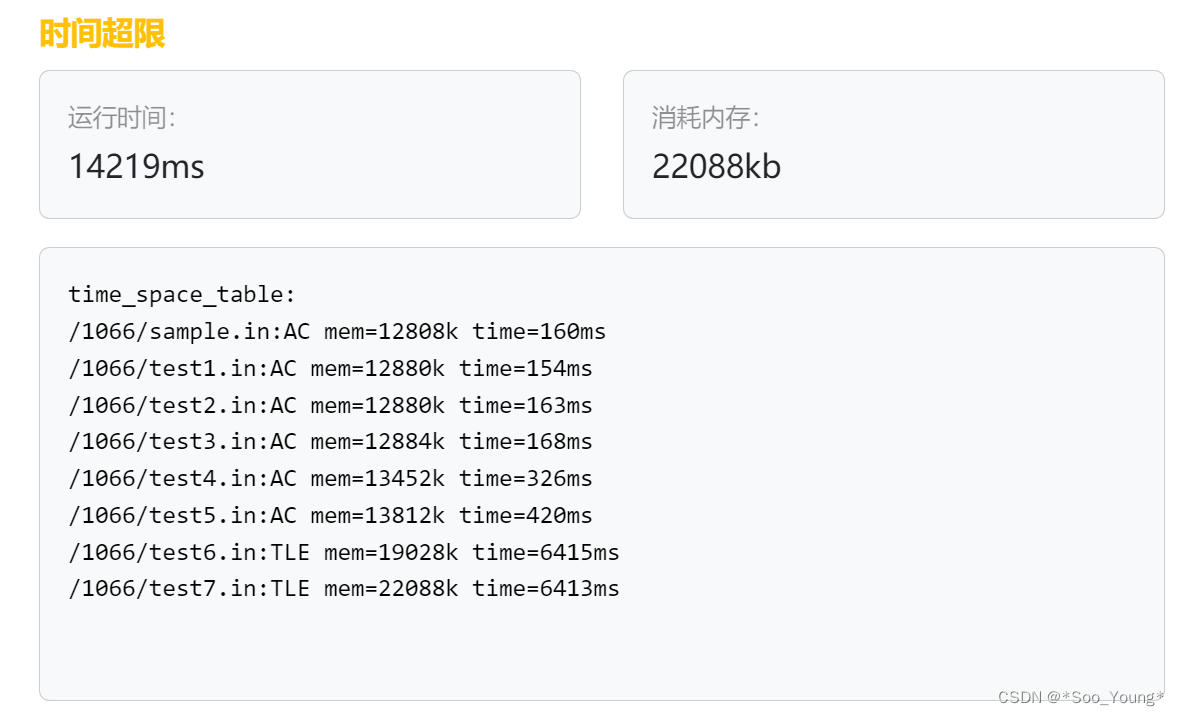
为什么会超时呢？试想一下，如果第一个物品有十个，那就遍历十次，没啥问题，那如果有一百个，一千个，一万个呢？那真的要遍历这么多次吗？

先来看一个例子，比如说容量为 5，有 1 种矿石，重量为 2，价值为 3，共有 10 个，即输入是：

5 1 2 3 10

查看输出的结果：

0 0 3 3 3 3 
0 0 3 3 6 6 
0 0 3 3 6 6 
0 0 3 3 6 6 
0 0 3 3 6 6 
0 0 3 3 6 6 
0 0 3 3 6 6 
0 0 3 3 6 6 
0 0 3 3 6 6 
0 0 3 3 6 6 

其实从第三行开始就没有什么区别了，这是为什么呢？物品价值为 2，第三行就是尝试将 3 个物品放入背包中，但是背包的总容量为 5，所以后面的遍历其实是没有意义的。

这样其实就知道，对于一个物品只需要遍历 k * weight[i] <= 背包容量 的部分就可以了，因为后面的部分和这些是完全一样的，基于这个思路再来改造一下代码。

for(int i = 0; i < N; i++) { // 遍历物品for(int j = dp.length - 1; j >= weight[i]; j--) { // 遍历背包容量for (int k = 1; k <= number[i] && (j - k * weight[i]) >= 0; k++) { dp[j] = max(dp[j], dp[j - k * weight[i]] + k * value[i]);}}
}

这次提交上去就不会报错了。

<3> 代码

import java.util.*;
public class Main {public static void main(String[] args) {Scanner sc = new Scanner(System.in);int C = sc.nextInt(); // 宇航舱的最大容量int N = sc.nextInt(); // 矿石的种类int[] weight = new int[N];int[] value = new int[N];int[] number = new int[N];int[] dp = new int[C + 1];int totalNum = 0; for (int i = 0; i < N; i++) weight[i] = sc.nextInt();for (int i = 0; i < N; i++) value[i] = sc.nextInt();for (int i = 0; i < N; i++) number[i] = sc.nextInt();for (int i = 0; i < N; i++) {for (int j = C; j >= weight[i]; j--) {for (int k = 1; k <= number[i] && (j - k * weight[i]) >= 0; k++) { // 遍历背包dp[j] = Math.max(dp[j], dp[j - k * weight[i]] + k * value[i]);}  }}System.out.println(dp[C]);}
}