今日题目：

• 104. 二叉树的最大深度
• 111. 二叉树的最小深度
• 110. 平衡二叉树
• 257. 二叉树的所有路径
• 112. 路径总和

今天做的题目主要围绕在二叉树的题目中常见的几个概念：深度、高度、路径。

• 求深度：设置一个全局遍历 deepth 表示递归调用过程中当前的深度，初始化为 0，对二叉树做递归遍历，每次递归进入左子树和右子树之前 deepth++，从左子树和右子树递归出来之后 deepth--。
• 求高度：空节点高度为 0，递归遍历的后序位置上，当前高度 height = max(leftHeight, rightHeight) + 1。
• 路径：也就是二叉树“根节点”到“叶子节点”的整条路径。这里可以利用一个性质：后序迭代遍历中，到达叶子节点时的 stack 就是从最上面的根节点到这个叶子节点的路径。其实，后序迭代遍历中，迭代到任何一个节点时的 stack 都是最上面的根节点到当前节点的路径。利用这个性质，我们就能很方便地找到我们想要找的路径，关键难点在于需要流畅地写出后序遍历的迭代版代码。

今天整体难度不大，这几个思路也很常见，属于基础。

Problem 1：树的深度

LC 104. 二叉树的最大深度 【easy】

104. 二叉树的最大深度 | LeetCode

难度不大，但借助这个题可以看出求深度的一个思路：

LC 111. 二叉树的最小深度 【易错】

111. 二叉树的最小深度 | LeetCode

这个题目有个易错点：需要明确好叶子节点指的是左右子树都是 null 的节点。而且这个题目要求的深度是指根节点到叶子节点的深度：

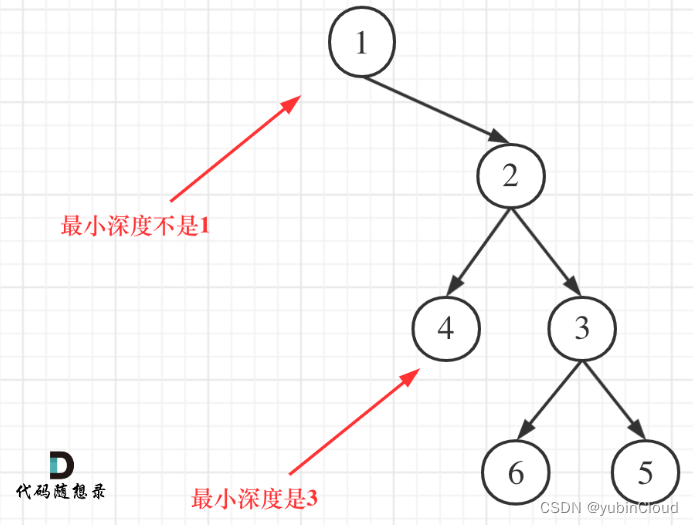
注意好这些易错点，代码架构与上一个题就差不多了：

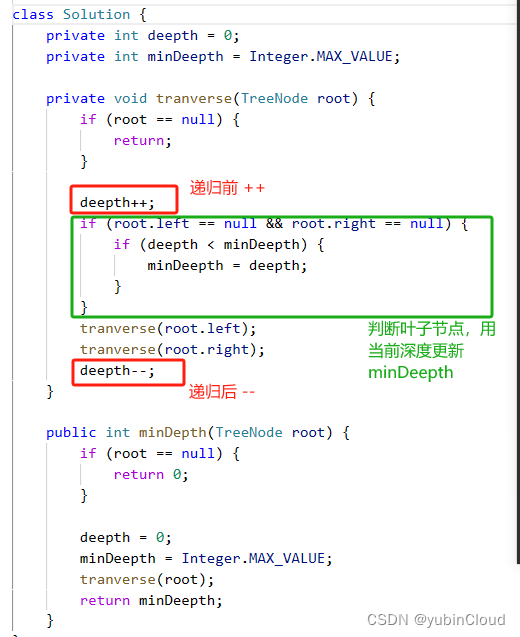
Problem 2：树的高度

LC 110. 平衡二叉树 【easy】

110. 平衡二叉树 | LeetCode

这个题目计算左右子树的高度并判断是否符合平衡二叉树的要求，关键就在于求高度。

按照思路来就可以，难度不大。

Problem 3：树的路径

这里主要可以利用：在后续迭代遍历中，迭代到某一个节点时，stack 中的节点序列就是根节点到这个节点的路径。按照这个思路，只要会写后续迭代遍历的代码，难度就不大了。

当然，可以利用递归的方式来获得路径，只需要在递归函数中加一个全局变量 path 来维护当前的路径即可，难度也不大。

LC 257. 二叉树的所有路径 【easy】

257. 二叉树的所有路径 | LeetCode

这个只需要使用后续迭代遍历，并在每一个叶子节点上将当前路径加入到结果集合中就可以了：

LC 112. 路径之和 【easy】

112. 路径总和

与上一个题目类似，难度也不大。