数据结构：红黑树的模拟实现

目录

1、什么是红黑树？

2、红黑树的相关操作与实现

1、节点定义

2、查找操作

3、插入操作

1、cur为红，p为红，g为黑，cur存在且为红

2、cur为红，p为红，g为黑，u不存在/u存在且为黑

4、判断是否为红黑树

3、完整实现代码

1、什么是红黑树？

        前面的文章我们讲解了AVL树，AVL树是一棵绝对平衡的二叉搜索树，其要求每个节点的左右子树高度差的绝对值都不超过1，这样可以保证查询时高效的时间复杂度。但是AVL树为了保持平衡要旋转来操作，在删除时有可能要一直旋转到根部，效率就会比较低下，如果数据的个数为静态的(即不会改变)，可以考虑AVL树，如果一个结构经常修改，那么红黑树是个不错的选择。

        红黑树（Red-Black Tree）是一种自平衡的二叉搜索树，它在普通的二叉搜索树的基础上增加了一些额外的规则来确保树的高度差别不会太大，从而保持了较为稳定的性能。在每个结点上增加一个存储位表示结点的颜色，可以是Red或 Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出俩倍，因而是接近平衡的。

红黑树的性质：

1、每个节点不是黑色就是红色。

2、根节点是黑色的。

3、如果一个节点是红色的，那么它的两个孩子是黑色的，也就是说，不可以有两个连续的红色节点。

4、对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点 

5、每个叶子结点都是黑色的(此处的叶子结点指的是空结点)

为什么满足上面的性质，红黑树就能保证：其最长路径中节点个数不会超过最短路径节点
个数的两倍？
因为不会有两个连续的红色节点，而每条路径上面的黑色节点数目都相同，所以所有节点的长度只会在：
N为每条路径黑色节点的个数，而红色节点最多也为N，所以所有路径的长度只会在N~2N内。

2、红黑树的相关操作与实现

红黑树与AVL树都是二叉搜索树，在插入操作时也使用了左旋与右旋，这些在AVL树的文章中也做过讲解，可以参考这篇文章：数据结构：AVL树

1、节点定义

enum Color
{RED,BLACK
};
template<class valuetype>
struct RBTreeNode
{RBTreeNode(const valuetype& data = valuetype(), Color color = RED):_left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _color(color){}RBTreeNode<valuetype>* _left;RBTreeNode<valuetype>* _right;RBTreeNode<valuetype>* _parent;valuetype _data;Color _color;};

使用枚举类型来表示颜色，节点结构与AVL树类似 

2、查找操作

红黑树的查找操作与二叉搜索树一致

a、从根开始比较，查找，比根大则往右边走查找，比根小则往左边走查找。

b、最多查找高度次，走到到空，还没找到，这个值不存在。

3、插入操作

红黑树是在二叉搜索树的基础上附加了平衡条件来保持特性，其最长路径中节点个数不会超过最短路径节点个数的两倍，所以它的旋转次数相对AVL树会少一些，而深度相比AVL树也不会很大，对于计算机来说，查找20次和查找40次是差别不大的。

在寻找插入位置方面与AVL树一致，只不过在调整保持特性有所不同。

接下来cur表示当前节点，p表示该节点的父节点，g表示该节点的爷爷节点，也就是父节点的父节点，u表示叔叔节点，也就是父节点的兄弟节点。

1、cur为红，p为红，g为黑，cur存在且为红

p是g的左孩子还是右孩子操作都是一样的

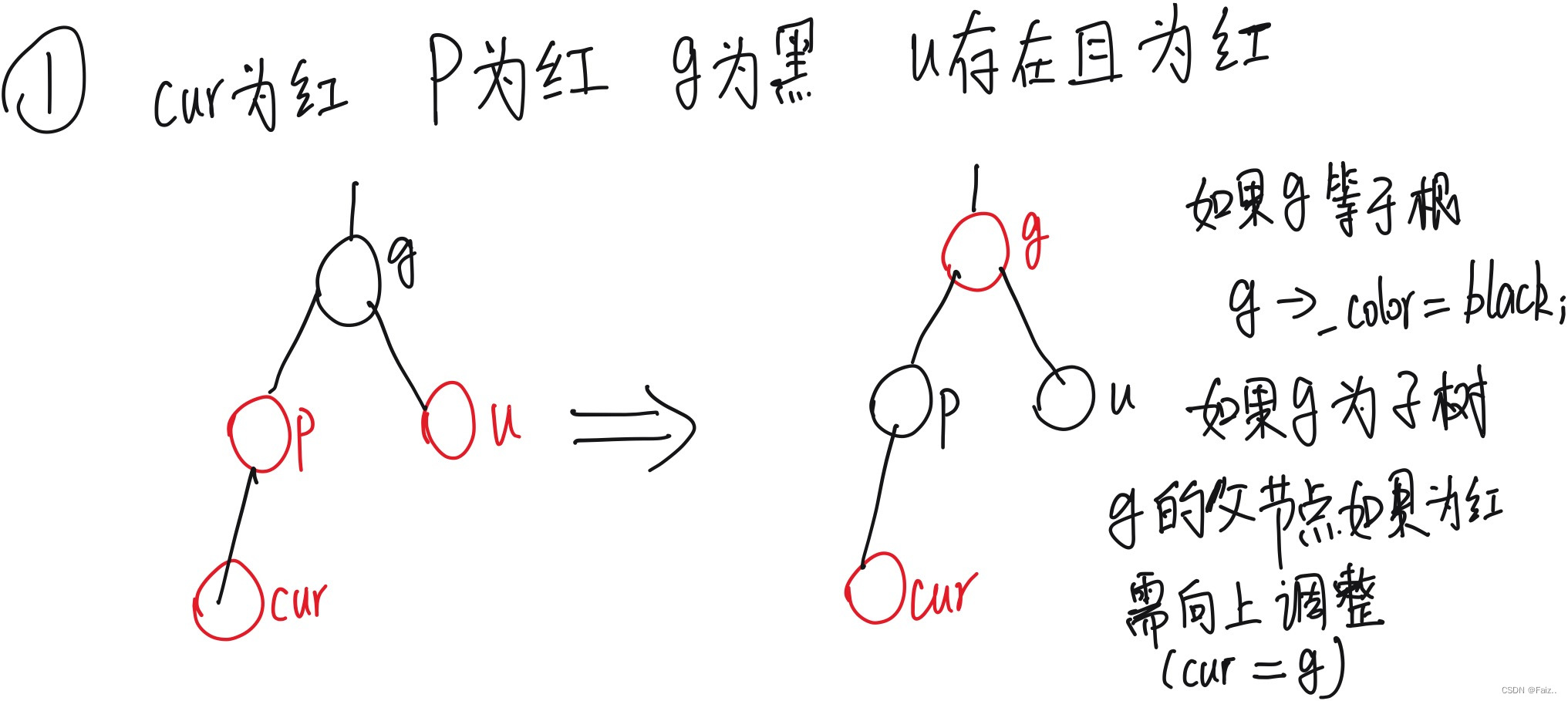
这种情况如图所示，将g节点变红，p节点和u节点变黑来保证性质4不变。

如果g的父节点为红，就违反了性质3，需要继续向上调整。

2、cur为红，p为红，g为黑，u不存在/u存在且为黑

1、如果u不存在，那么cur一定是新增节点，由性质4可以得到。

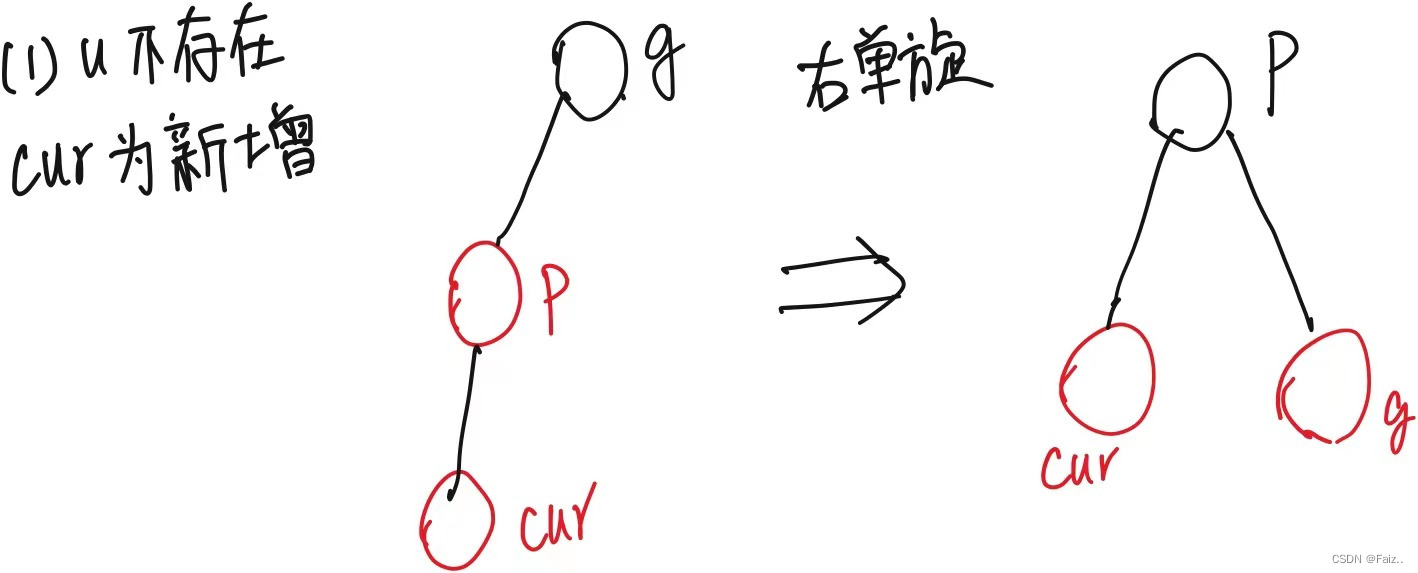
如果p是g的左孩子，cur为左孩子则进行右单旋。

相反如果p是g的右孩子，cur为右孩子则进行左单旋。

2、如果u存在且为黑，那么cur一定是由（1、cur为红，p为红，g为黑，cur存在且为红）这种情况调整上来的，也是根据性质4就可以推出来，每条路径上的黑色节点数目是相同的。

接下来只需要判断需要进行左单旋还是右单旋即可：

🚀p是g的左孩子，cur是p的左孩子

🚀p是g的右孩子，cur是p的右孩子

 

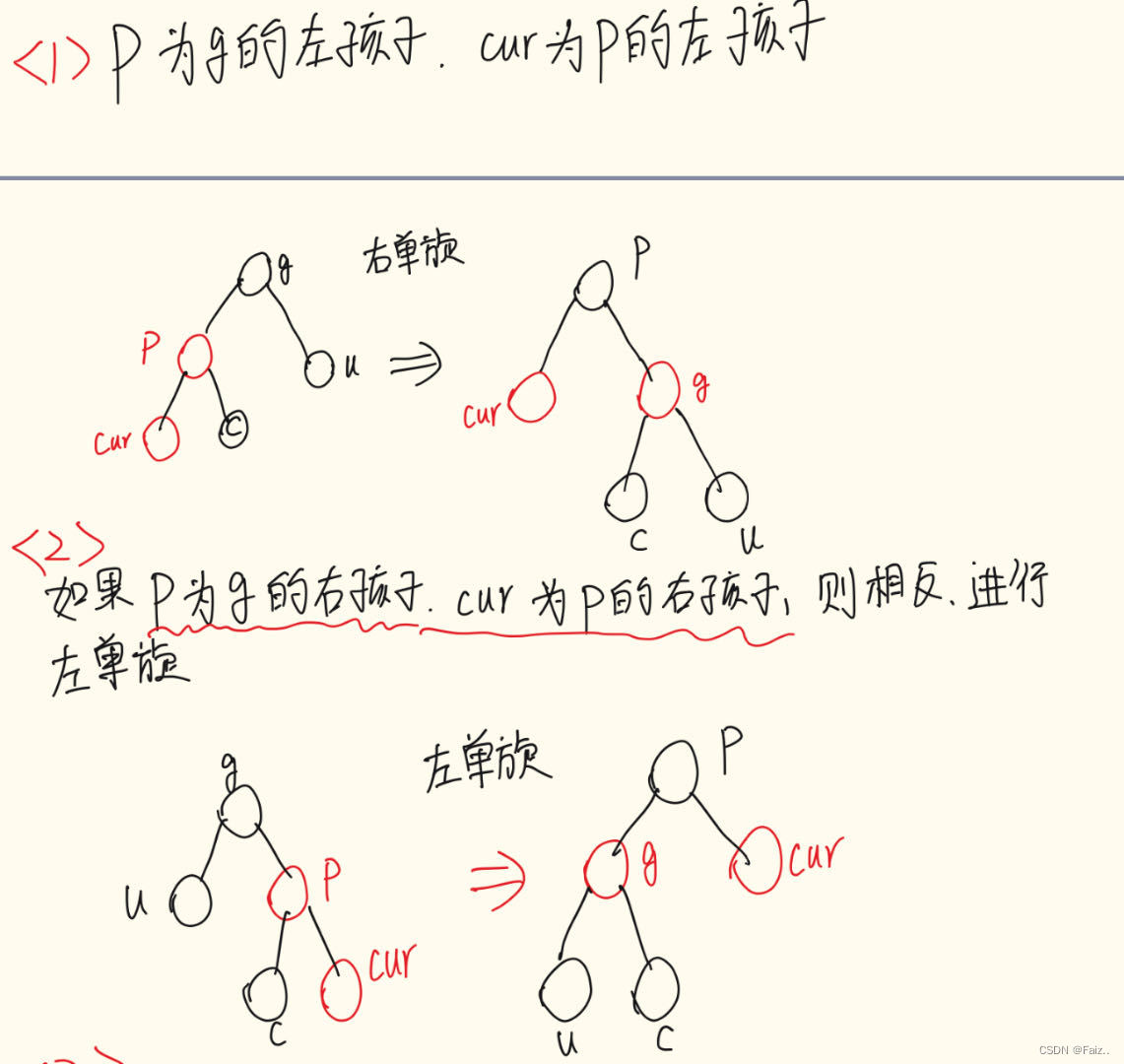
为保证性质4，调整p为黑，g为红。 

🚀p是g的右孩子，cur是p的左孩子

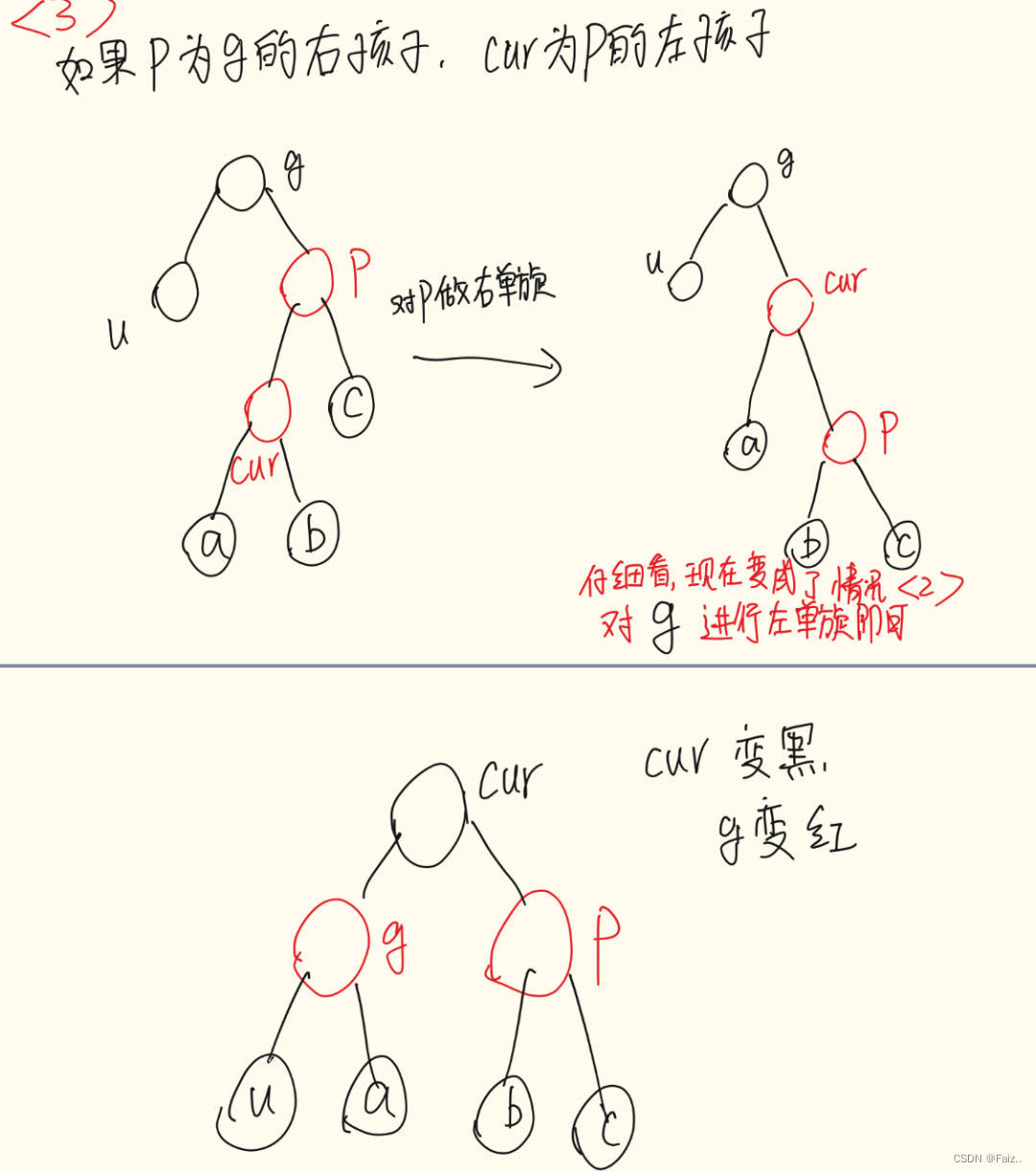
对p做右单旋后，仔细观察发现转变为了情况<2>，对g进行左单旋即可。

为保证性质4，调整cur为黑，g为红。

🚀p是g的左孩子，cur是p的右孩子

 对p做左单旋后，仔细观察发现转变为了情况<1>，对g进行右单旋即可。

为保证性质4，调整cur为黑，g为红。

根据上述逻辑写出插入操作，代码如下：

bool Insert(const  valuetype& data){if (_root == nullptr){_root = new Node(data, BLACK);//根的双亲为头结点return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_data < data){parent = cur;cur = cur->_right;}else if(cur->_data>data){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(data, RED);if (cur->_data < parent->_data){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent && parent->_color == RED){Node* grandparent = parent->_parent;if (parent == grandparent->_left){Node* uncle = grandparent->_right;if (uncle && uncle->_color == RED){grandparent->_color = RED;parent->_color = BLACK;uncle->_color = BLACK;cur = grandparent;parent = cur->_parent;}else{if (cur == parent->_left){RotateR(grandparent);parent->_color = BLACK;grandparent->_color = RED;}else{RotateL(parent);RotateR(grandparent);cur->_color = BLACK;grandparent->_color = RED;}break;}}else{Node* uncle = grandparent->_left;if (uncle && uncle->_color == RED){grandparent->_color = RED;parent->_color = BLACK;uncle->_color = BLACK;cur = grandparent;parent = cur->_parent;}else{if (cur == parent->_right){RotateL(grandparent);parent->_color = BLACK;grandparent->_color = RED;}else{RotateR(parent);RotateL(grandparent);cur->_color = BLACK;grandparent->_color = RED;}break;}}}_root->_color = BLACK;return true;}

4、判断是否为红黑树

我们主要验证性质3和性质4 

bool Check(Node* root, int blacknum, const int refval){if (root == nullptr){if (blacknum != refval){cout << "有黑色节点数目不同的路径";return false;}return true;}if (root->_color == RED && root->_parent->_color == RED){cout << "存在连续的红色节点";return false;}if (root->_color == BLACK){blacknum++;}return Check(root->_left, blacknum, refval)&& Check(root->_right, blacknum, refval);}

每次一条路径走完时，我们需要把它和一个标准值来比较，验证性质4.

我们走完一条路径得到标准值refval来调用Check递归函数检查。

//判断是否为红黑树bool IsRBTree(){if (_root == nullptr)return true;if (_root->_color == RED)return false;Node* cur = _root;int refval = 0;while (cur){if (cur->_color == BLACK)refval++;cur = cur->_left;}return Check(_root, 0, refval);  //调用检查函数，black为0；}

3、完整实现代码

#pragma onceenum Color
{RED,BLACK
};
template<class valuetype>
struct RBTreeNode
{RBTreeNode(const valuetype& data = valuetype(), Color color = RED):_left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _color(color){}RBTreeNode<valuetype>* _left;RBTreeNode<valuetype>* _right;RBTreeNode<valuetype>* _parent;valuetype _data;Color _color;};template<class valuetype>
class RBTree
{
public:typedef RBTreeNode<valuetype> Node;bool Insert(const  valuetype& data){if (_root == nullptr){_root = new Node(data, BLACK);//根的双亲为头结点return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_data < data){parent = cur;cur = cur->_right;}else if(cur->_data>data){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(data, RED);if (cur->_data < parent->_data){parent->_left = cur;}else{parent->_right = cur;}cur->_parent = parent;while (parent && parent->_color == RED){Node* grandparent = parent->_parent;if (parent == grandparent->_left){Node* uncle = grandparent->_right;if (uncle && uncle->_color == RED){grandparent->_color = RED;parent->_color = BLACK;uncle->_color = BLACK;cur = grandparent;parent = cur->_parent;}else{if (cur == parent->_left){RotateR(grandparent);parent->_color = BLACK;grandparent->_color = RED;}else{RotateL(parent);RotateR(grandparent);cur->_color = BLACK;grandparent->_color = RED;}break;}}else{Node* uncle = grandparent->_left;if (uncle && uncle->_color == RED){grandparent->_color = RED;parent->_color = BLACK;uncle->_color = BLACK;cur = grandparent;parent = cur->_parent;}else{if (cur == parent->_right){RotateL(grandparent);parent->_color = BLACK;grandparent->_color = RED;}else{RotateR(parent);RotateL(grandparent);cur->_color = BLACK;grandparent->_color = RED;}break;}}}_root->_color = BLACK;return true;}void RotateL(Node* parent){Node* sub = parent->_right;Node* subl = sub->_left;parent->_right = subl;sub->_left = parent;Node* ppnode = parent->_parent;parent->_parent = sub;if (subl){subl->_parent = parent;}if (parent == _root){_root = sub;sub->_parent = nullptr;}else{if (parent == ppnode->_left){ppnode->_left = sub;}else{ppnode->_right = sub;}sub->_parent = ppnode;}}void RotateR(Node* parent){Node* subl = parent->_left;Node* subr = subl->_right;parent->_left = subr;if (subr){subr->_parent = parent;}subl->_right = parent;Node* ppnode = parent->_parent;parent->_parent = subl;if (parent == _root){_root = subl;subl->_parent = nullptr;}else{if (parent == ppnode->_left){ppnode->_left = subl;}else{ppnode->_right = subl;}subl->_parent = ppnode;}}bool Check(Node* root, int blacknum, const int refval){if (root == nullptr){if (blacknum != refval){cout << "有黑色节点数目不同的路径";return false;}return true;}if (root->_color == RED && root->_parent->_color == RED){cout << "存在连续的红色节点";return false;}if (root->_color == BLACK){blacknum++;}return Check(root->_left, blacknum, refval)&& Check(root->_right, blacknum, refval);}//判断是否为红黑树bool IsRBTree(){if (_root == nullptr)return true;if (_root->_color == RED)return false;Node* cur = _root;int refval = 0;while (cur){if (cur->_color == BLACK)refval++;cur = cur->_left;}return Check(_root, 0, refval);  //调用检查函数，black为0；}void _inorder(Node* root){if (root == nullptr){return;}_inorder(root->_left);cout << root->_data<<" ";_inorder(root->_right);}void inorder(){_inorder(_root);}
private:Node* _root=nullptr;
};

以上就是对于红黑树的简单讲解，红黑树从根到叶子的最长路径不超过最短路径的两倍长。这确保了树的高度始终保持在对数级别，使得查找、插入和删除等操作的时间复杂度始终保持较低水平O(log n)。通过引入颜色标记和自平衡规则，提供了一种高效的二叉搜索树实现，适用于需要频繁插入、删除和查找操作的场景。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/742327.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

能发顶会！GNN结合LLMs的三大创新思路！新SOTA准确率提升10倍

能发顶会！GNN结合LLMs的三大创新思路！新SOTA准确率提升10倍

LLMs在处理NLP任务方面表现出色&#xff0c;而GNNs在挖掘和分析复杂关系数据&#xff08;图数据&#xff09;方面展现出其卓越的能力。这种趋势催生了将这两种技术整合的研究兴趣&#xff0c;为解决更多领域的实际问题。GNN结合LLMs也逐渐成为了研究的热点。 GNNLLMs可以发挥二…
阅读更多...
集智书童 | 炸裂 ！轻量化YOLO | ShuffleNetv2与Transformer结合，重塑YOLOv7成就超轻超快YOLO

集智书童 | 炸裂 ！轻量化YOLO | ShuffleNetv2与Transformer结合，重塑YOLOv7成就超轻超快YOLO

本文来源公众号“集智书童”&#xff0c;仅用于学术分享&#xff0c;侵权删&#xff0c;干货满满。 原文链接&#xff1a;炸裂 &#xff01;轻量化YOLO | ShuffleNetv2与Transformer结合&#xff0c;重塑YOLOv7成就超轻超快YOLO 随着移动计算技术的迅速发展&#xff0c;在移动…
阅读更多...
ECharts饼图图例消失踩的坑

ECharts饼图图例消失踩的坑

在使用Echarts的饼图时&#xff0c;当时做法是在图例数小于8时显示全部的图例&#xff0c;在大于8的时候显示前8个图例。于是用了两种不同的方式处理。导致出现切换时间后图例不显示的情况。 错误过程&#xff1a; 在进行图例生成时采用了两种不同的方式&#xff1a; ①如果…
阅读更多...
打造你的HTML5打地鼠游戏：零基础入门教程

打造你的HTML5打地鼠游戏：零基础入门教程

&#x1f31f; 前言 欢迎来到我的技术小宇宙&#xff01;&#x1f30c; 这里不仅是我记录技术点滴的后花园&#xff0c;也是我分享学习心得和项目经验的乐园。&#x1f4da; 无论你是技术小白还是资深大牛&#xff0c;这里总有一些内容能触动你的好奇心。&#x1f50d; &#x…
阅读更多...
Rust生命周期和生命周期声明‘作用Missing lifetime specifier

Rust生命周期和生命周期声明‘作用Missing lifetime specifier

Missing lifetime specifier&#xff1a;报错说明缺失声明周期声明 Rust 生命周期机制是与所有权机制同等重要的资源管理机制。 之所以引入这个概念主要是应对复杂类型系统中资源管理的问题。 引用是对待复杂类型时必不可少的机制&#xff0c;毕竟复杂类型的数据不能被处理器…
阅读更多...
UDP连接树莓派时提高连接速度，降低卡顿感

UDP连接树莓派时提高连接速度，降低卡顿感

背景 树莓派4B刷的是ubuntu20.4系统&#xff0c;使用win10自带的远程桌面连接和其连接&#xff0c;卡的一批&#xff0c;于是探索并记录下如何降低连接卡顿感 步骤一 点击显示选项&#xff0c; 降低显示配置和颜色深度&#xff1a; 步骤二 我的树莓派是通过电脑移动热点的方式…
阅读更多...
Qt+FFmpeg+opengl从零制作视频播放器-13.打包为exe包发布软件

Qt+FFmpeg+opengl从零制作视频播放器-13.打包为exe包发布软件

1.首先visual studio给生成程序添加桌面图标。 右键工程，添加新文件资源文件Resource.rc 选择导入文件，我这里导入了Player.ico文件。 添加后，在资源文件那里就可以看见ico文件。 然后编译release程序， 生成的可执行程序就带上了图标。 2.使用Qt 程序打包发布-windeployq…
阅读更多...
AWS入门实践－AWS CLI工具的使用介绍

AWS入门实践－AWS CLI工具的使用介绍

AWS CLI&#xff08;Amazon Web Services Command Line Interface&#xff09;是一个强大的工具&#xff0c;它允许您直接从命令行与AWS服务进行交互。这不仅可以加快许多任务的处理速度&#xff0c;而且还可以通过脚本自动化。 一、AWS CLI工具的安装 1、Windows 安装下载…
阅读更多...
uniapp图片涂鸦插件(支持多种涂鸦方式，图片放大缩小)

uniapp图片涂鸦插件(支持多种涂鸦方式，图片放大缩小)

工程地址https://gitee.com/geshijia/ct-graffiti ct-graffiti涂鸦组件使用说明 参考说明 参考链接&#xff1a;https://github.com/ylyuanlu/yl-graffiti 感谢作者的付出&#xff0c;给我提供了一些思路&#xff0c;并做了如下优化&#xff1a; 增加图片放大缩小移动功能添…
阅读更多...
第十四届蓝桥杯蜗牛

第十四届蓝桥杯蜗牛

蜗牛 线性dp 目录 蜗牛 线性dp 先求到达竹竿底部的状态转移方程 求蜗牛到达第i根竹竿的传送门入口的最短时间​编辑 题目链接&#xff1a;蓝桥杯2023年第十四届省赛真题-蜗牛 - C语言网 关键在于建立数组将竹竿上的每个状态量表示出来&#xff0c;并分析出状态转移方程 in…
阅读更多...
[实战]API防护破解之签名验签

[实战]API防护破解之签名验签

前言&#xff1a; 传统的接口在传输的过程中&#xff0c;是非常容易被抓包进行篡改&#xff0c;从而进行中间人攻击。这时候我们可以通过对参数进行签名验证&#xff0c;如果参数与签名值不匹配&#xff0c;则请求不通过&#xff0c;直接返回错误信息&#xff0c;从而防止黑客…
阅读更多...
混合A*源码解读（c++）

混合A*源码解读（c++）

基于ros中通过slam建立的栅格地图&#xff0c;使用混合A*进行路径规划。 首先是run_hybrid_astar.cpp: #include "hybrid_a_star/hybrid_a_star_flow.h" #include "3rd/backward.hpp" #include <ros/ros.h>namespace backward { backward::SignalHa…
阅读更多...
带钢切割控制液压比例阀放大器

带钢切割控制液压比例阀放大器

比例阀控制器放大器放大板技术是电液比例控制系统中的重要组成部分&#xff0c;它负责对比例阀进行精确控制&#xff0c;以实现对液压系统中流量、压力等参数的精细调节。可以实现对液压流量或压力的精确控制&#xff0c;从而使系统以更高的精度和更快的响应速度执行各种操作。…
阅读更多...
以102flowers数据集为例训练ResNet50模型

以102flowers数据集为例训练ResNet50模型

以102flowers数据集为例训练ResNet50模型 使用飞桨高阶API&#xff0c;使用最少的代码量&#xff0c;实现在102flowers数据集训练ResNet50模型。同时可以一条命令修改成Mnist、Cifar10、Cifar100等数据集&#xff0c;换成其它模型也是只需要一句话代码。 数据集介绍 102flowe…
阅读更多...
Zoho Mail有微信小程序啦！从微信就能直接收发邮件

Zoho Mail有微信小程序啦！从微信就能直接收发邮件

Zoho Mail有微信小程序啦&#xff01;从微信就能直接收发邮件。可实现&#xff1a;从微信直接查看邮件、撰写新邮件、回复邮件。对于那些想从手机访问Zoho Mail企业邮箱来收发邮件&#xff0c;但又不想下载Zoho Mail 的手机app来占用手机存储的用户来说&#xff0c;微信小程序实…
阅读更多...
Celery知识

Celery知识

celery介绍 # celery 的概念&#xff1a; * 翻译过来是芹菜 * 官网&#xff1a;https://docs.celeryq.dev/en/stable/ # 是分布式的异步任务框架&#xff1a; 分布式&#xff1a;一个任务&#xff0c;拆成多个任务在不同机器上做 异步任务&#xff1a;后台执行…
阅读更多...
【开源】SpringBoot框架开发软件学院思政案例库系统

【开源】SpringBoot框架开发软件学院思政案例库系统

目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 系统管理员2.2 普通教师 三、系统展示四、核心代码4.1 查询思政案例4.2 审核思政案例4.3 查询思政课程4.4 思政案例点赞4.5 新增思政案例评语 五、免责说明 一、摘要 1.1 项目介绍 基于JAVAVueSpringBootMySQL的软件学…
阅读更多...
Mysql8.0.30数据data目录文件解释

Mysql8.0.30数据data目录文件解释

数据库内存和磁盘架构 data目录展示 [rootDESKTOP-9ADRUGP data]# pwd /usr/local/software/mysql/3312/data [rootDESKTOP-9ADRUGP data]# ls -l total 96616 -rw-r----- 1 systemd-coredump input 56 Jul 24 2023 auto.cnf -rw-r----- 1 systemd-coredump input 30…
阅读更多...
数据库基础理论知识

数据库基础理论知识

1.基本概念 数据(Data)&#xff1a;数据库存储的基本对象。数字、字符串、图形、图像、音频、视频等数据库(DB)&#xff1a;在计算机内&#xff0c;永久存储、有组织、可共享的数据集合数据库管理系统(DBMS)&#xff1a;管理数据库的系统软件数据库系统(DBS)&#xff1a;DBDBM…
阅读更多...
浏览器的工作原理

浏览器的工作原理

从输入一个url到页面加载完成&#xff0c;中间都发生了什么&#xff1f; 参考原文地址 首先在浏览器地址栏输入一个地址并回车之后&#xff0c; 1. DNS查找 浏览器会进行DNS查找&#xff0c;把域名https://example.com转化为真实的IP地址10.29.33.xx&#xff0c;根据IP地址找…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023