上一篇介绍了窄带波束形成,当信号的带宽增加,窄带波束形成的性能会降低很多。
首先从窄带beamforming说起
阵列模式:M个阵元组成的线性阵列
当有个输入信号
,
,对应的信号的入射方向为
,
。第一个信号
是感兴趣信号,其他信号是干扰信号。每一个信号对应的方向向量
的表达式为:
![]()
理想情况下,我们的目标是为感兴趣的信号构造一个固定的响应,并且使得干扰信号的响应是0。为了简化,在这里不考虑噪声。如上的条件可以通过一个矩阵方程描述:

显然,只要等式左边的矩阵是满秩,总能够找到一组阵列权重将M-1个干扰信号消除。满足完全消除的阵列权重的值依赖与信号的频率和信号的到达方向。
对于宽带信号,每一个信号包含无限多不同频率成分,对于不同的频率而言,阵列权重值不同。可以将权重矩阵写成如下形式,对于每一个频率对应的权重:
![]()
对于不同的频率,都需要计算一个,窄带波束形成处理宽带信号显然效率很低。
宽带波束形成器的结构
有两类获取频率相关的权重的方法:
- 传感器延时线SDLs(sensor delay-lines)
- 抽头延时线TDLs(tapped delay-lines)或者FIR/IIR滤波器
我们介绍第2种方法:TDLs。TDLs和FIR/IIR滤波器是通过执行时域滤波过程,为每一个接收到的宽带传感器信号,构造频率相关的响应,从而补偿不同频率成分的相位差。这种结构如下图所示。

上图的宽带波束形成器结构对波场进行空间和时间的采样。宽带波束形成器可以表示成:
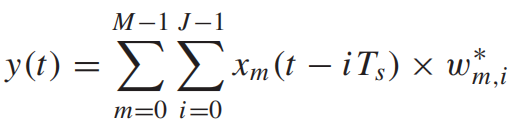
是阵元的个数,
是每个阵元通道的延时单元的个数。
是相邻抽头的延时(对于数字信号就是采样时间)
将宽带波束形成器表示为矩阵的形式
![]()
一共有
乘以
个权重系数
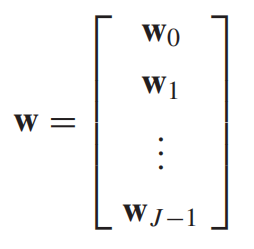
每一个列向量,
包含
个复共轭系数,位于M抽头延时线的第
个抽头
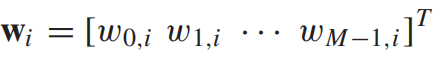
同样输入信号可以表示为一个列向量:
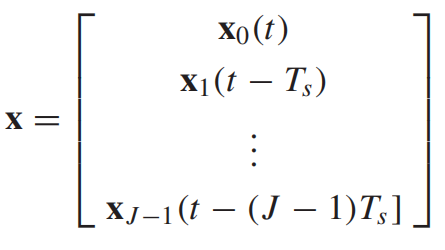
,
是M个阵列的第
个延时数据
当时,就变成了窄带波束形成。
宽带beamformer的波束响应
对于复平面波信号,假设
,则
![]() ,
,
注意这里是小写并且没有加粗,
代表阵元的编号。
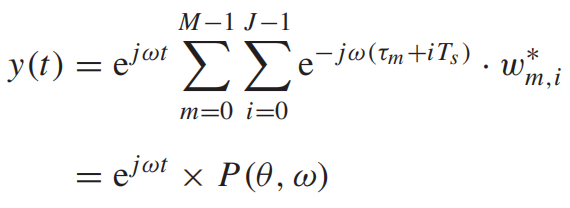
是波束响应,与信号的频率和角度相关,用向量表式:
![]()
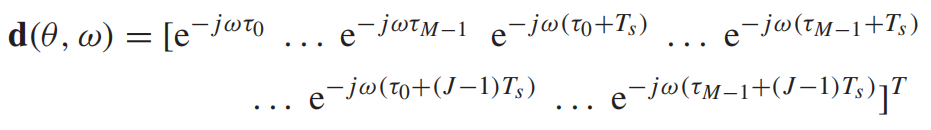
是转向向量,长度为
乘以
。
当时,就变成了窄带波束形成中介绍的转向向量了。
类似上一篇介绍的窄带波束形成,现在对阵列进行规定:
线性阵列,阵元间距是,
,
为了避免空域混叠,,
是信号最高频率成分
对应的波长。假定阵列可操作的频率
,并且
,
。
是波的速度
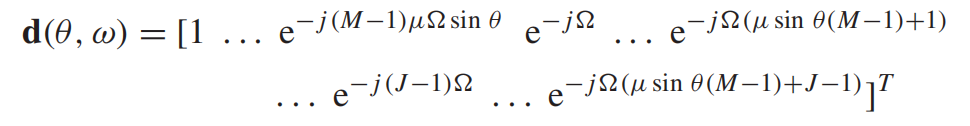
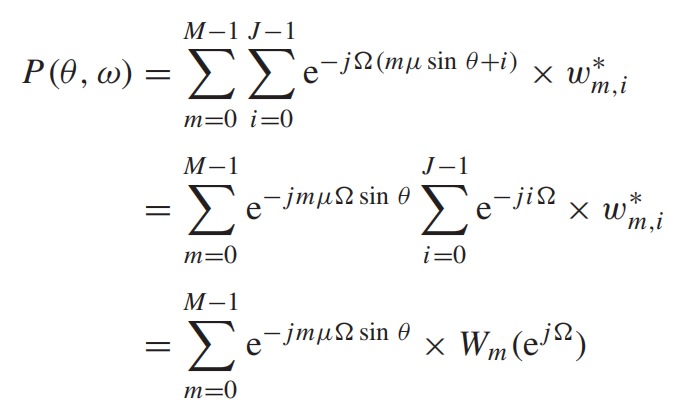
![]() 是第m个阵元的抽头延时线(FIR滤波器)系数的离散傅里叶变换。当
是第m个阵元的抽头延时线(FIR滤波器)系数的离散傅里叶变换。当且
,则
。
是信号最高频率成分对应的采样周期。
宽带波束形成的波束响应与信号入射角以及
(
)有关。
参考:Wei Liu《Wideband Beamforming》University of Sheffifield, UK









)









