论文题目:A dynamic multi-objective optimization based on a hybrid of pivot points prediction and diversity strategies
基于枢轴点预测和多样性策略混合的动态多目标优化(Jinhua Zheng a,b,d, Fei Zhou a,b,∗, Juan Zou a,b, Shengxiang Yang a,e, Yaru Hu a,c)Swarm and Evolutionary Computation 78 (2023) 101284
刚开始学习多目标优化算法,不作商业用途,如果有不正确的地方请指正!
个人总结:
挺简单明了又高效的算法
三个部分双重预测+多种群:
预测一:在目标空间根据找到每个目标轴的极值点作为参考点然后找到枢轴线不断扩充点,在环境变化时,根据前时刻的情况对下一个时刻的枢轴点进行预测
预测二:根据种群前两个时刻的中心点进行预测,在监测到环境变化不相似时,中心点的移动长度乘一个随机数L.(好像文章中没有讲到怎么判断环境变化是否相似)
多种群:根据前面时刻的种群确定每个决策变量的最大值最小值在进行随机产生解,相比直接产生随机解增加了一点点收敛性(如果ps值的的变化趋势时变大的情况这个策略可靠吗?).
随机选取了种群中5 %的个体作为检测器来检测环境变化。如果目标值之间存在不匹配,则将其视为环境改变了
Ppiv(枢轴点)和Prand(多种群产生的解的数量)的大小分别设置为0.3 N和0.7 N。
引言
目前存在的问题
基于多样性方法的劣势:
在处理复杂的环境变化时,这些策略并不能提供良好的性能,尤其是不规则变化的PF或PS
基于内存方法的劣势:
对于非周期性问题,基于内存的策略可能会显示出较差的结果。
基于预测方法的劣势:
在基于预测的策略中设置不合适的预测方法或者模型会影响总体的收敛和分布,此外在处理快速变化的环境,其性能可能会随着优化的进行而迅速下降。
基于多种群方法:
前些日子复现的PBDMO就是多种群方法
本文提出的想法
提出了一种基于双重预测和多样性策略混合的动态多目标优化策略.
- 通过动态选择机制选择的一些个体(枢轴点)用于模拟PF或PS。然后,自回归模型预测环境变化后的枢轴点,以达到跟踪变化的PF或PS的目的
- 将环境变化分为相似和不同的变化。当变化相似时,非支配个体结合非支配个体集合中心点的运动趋势,预测环境变化后的非支配个体。否则,在利用非支配个体集合中心点的运动趋势对非支配个体进行预测的同时,对预测结果进行前后推导,推导新的最优解。
- 在相对准确的可行区域内随机生成搜索个体,在一定程度上提升了随机搜索个体的质量,可以保持种群的多样性
背景及相关工作
这里介绍了基础和DMOEA框架,在静态时使用RM-MEDA算法进行优化
提出框架与实施
提出了一种新的基于枢轴点预测的预测策略。在该预测策略中,如果检测到一个环境变化,那么对其做出响应的种群将由三个子种群组成。
A.Pivot point and predicting the pivot point set(枢轴点和预测合集)
首先初始化一个大小为N的种群,并建立一个存储池Q用于存储历史信息.然后在目标空间中通过动态选择机制迭代地选择枢轴点,并将枢轴点放入存储池Q中。下图展示了在一开始的三个时刻选择枢轴点的过程:
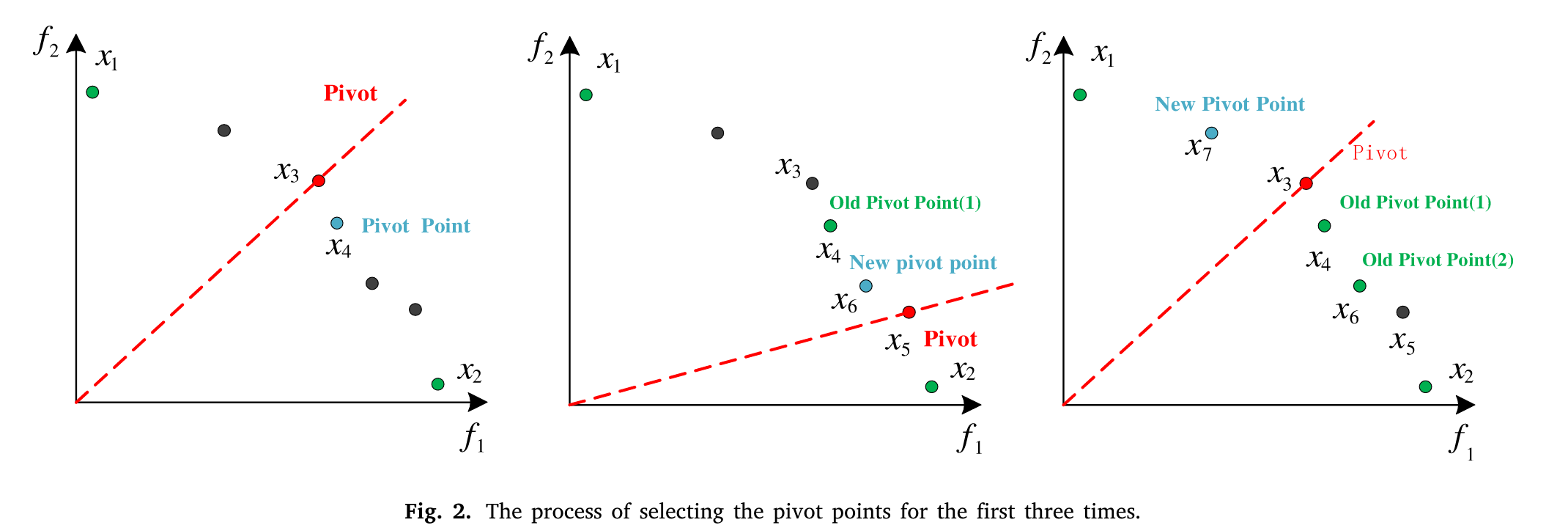
- (找到极值点)设第j个坐标轴上的极值点为xj,令xj为以Y = ( Y1 , Y2 , ... , Yn)T为坐标轴方向,最小化聚集函数g ( x | Y )的解。这里,n表示决策空间的维数。极值点的数学表达式如式( 3 )所示:
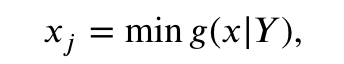 式中:x∈Ω;Y为坐标轴的权向量;J为第j维坐标轴。为了搜索第j个轴上的极值点,需要固定第j个维度上的方向,则第j个维度方向上的权重向量为wj = 1,其他方向上的权重向量为wn = 10e-6 。如图2所示,x1和x2是(标记为绿色的点)的极值点,x1和x2被放入Q中.此时,Q中有两个个体x1和x2 .
式中:x∈Ω;Y为坐标轴的权向量;J为第j维坐标轴。为了搜索第j个轴上的极值点,需要固定第j个维度上的方向,则第j个维度方向上的权重向量为wj = 1,其他方向上的权重向量为wn = 10e-6 。如图2所示,x1和x2是(标记为绿色的点)的极值点,x1和x2被放入Q中.此时,Q中有两个个体x1和x2 .
- (建立枢纽)建立枢轴的前提是找到种群中与存储池Q中所有个体距离之和最大的个体,并以原点建立枢轴,用公式
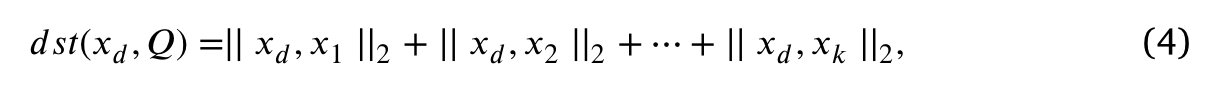 表达种群中个体xd与存储池Q中所有个体的距离之和.如图2所示,在第一次选择枢轴点的过程中,x3是种群中距离存储池Q中个体最远的个体。将x3与原点连接起来,形成一条称为支点的参考线。
表达种群中个体xd与存储池Q中所有个体的距离之和.如图2所示,在第一次选择枢轴点的过程中,x3是种群中距离存储池Q中个体最远的个体。将x3与原点连接起来,形成一条称为支点的参考线。
- (找到枢轴点)计算目标空间中的个体与枢轴L的距离,为保证所选枢轴个体的收敛性,距离枢轴最近的个体即为本次选择过程中的枢轴点。设个体P的坐标为( xk , yk)。个体P到支点L的距离的数学表达式如式( 6 )所示:

- 重复上述过程直到找到足够多的支点.
自回归预测模型对环境变化后的枢轴点进行预测,将枢轴点作为代表个体对PF或PS进行有效跟踪。支点的选取过程如算法1所示:

B.Predicting the non-dominant individual set(预测非支配个体集合)
环境变化时相似时
所有非支配点都会利用集合中心点的演化趋势进行演化。此时,t + 1时刻预测非支配个体的数学表达式如式( 7 )所示:
 Dcnonk t表示非支配个体集合中心点在时间步t的移动趋势。
Dcnonk t表示非支配个体集合中心点在时间步t的移动趋势。
环境变化不相似时
利用非支配个体的当前位置和非支配个体集合中心点的移动趋势来预测非支配个体的下一个时间步。同时,推导出预测的非支配个体。推导操作是基于预测结果进行的;预测结果随机向前和向后移动λ次Dcnonk t。推导预测结果的操作如图3所示。针对这种不相似变化的预测策略的数学表达式如下:


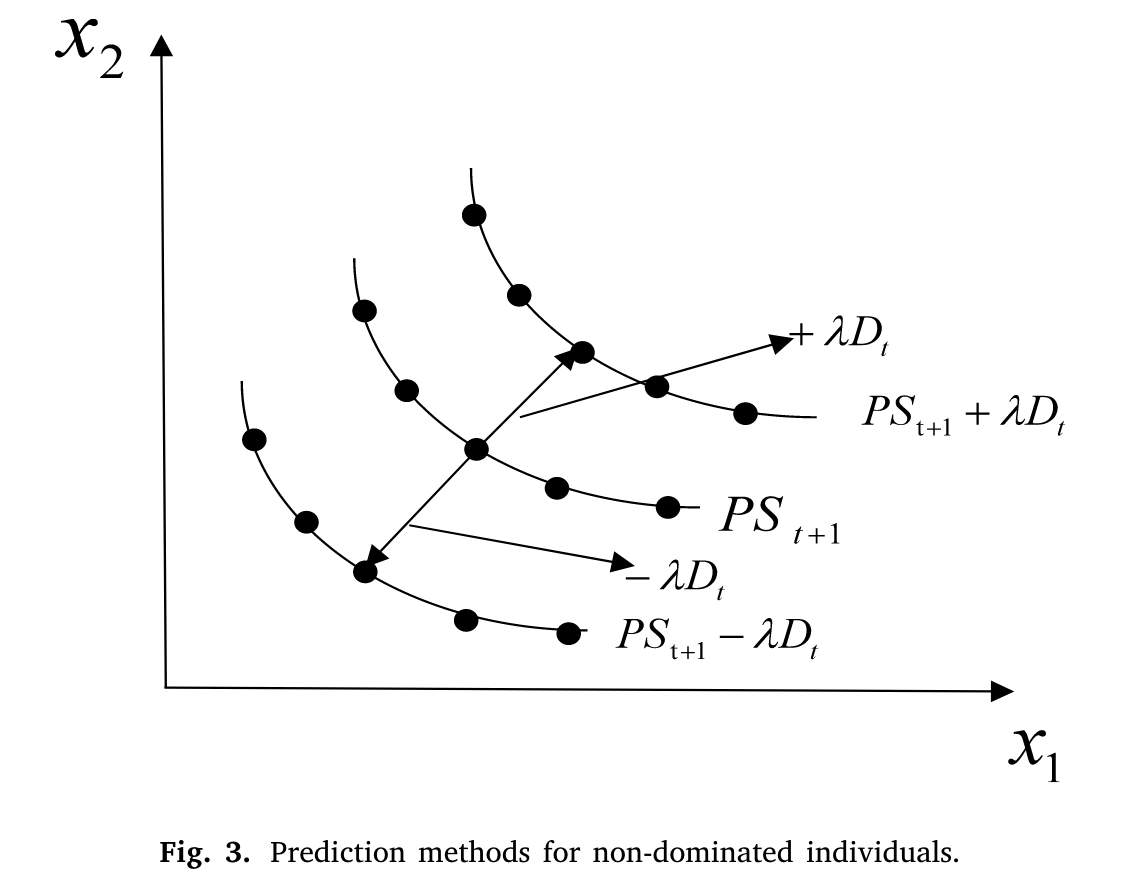
伪代码如下:

C.Generation mechanism of random search solutions to maintain population diversity(维持种群多样性的随机搜索生成机制)
假设随机搜索个体在决策空间中随机产生。在这种情况下,一些随机搜索个体可能会远离真实的PF,这种随机搜索个体的性能可能会影响种群的收敛性。如果能够明确随机搜索个体的生成区域,则可以在一定程度上降低该问题发生的概率。在前期工作的基础上,我们决定在通过预测得到的前两个子种群中选择最大值和最小值点来确定随机搜索个体的生成区域并运行.
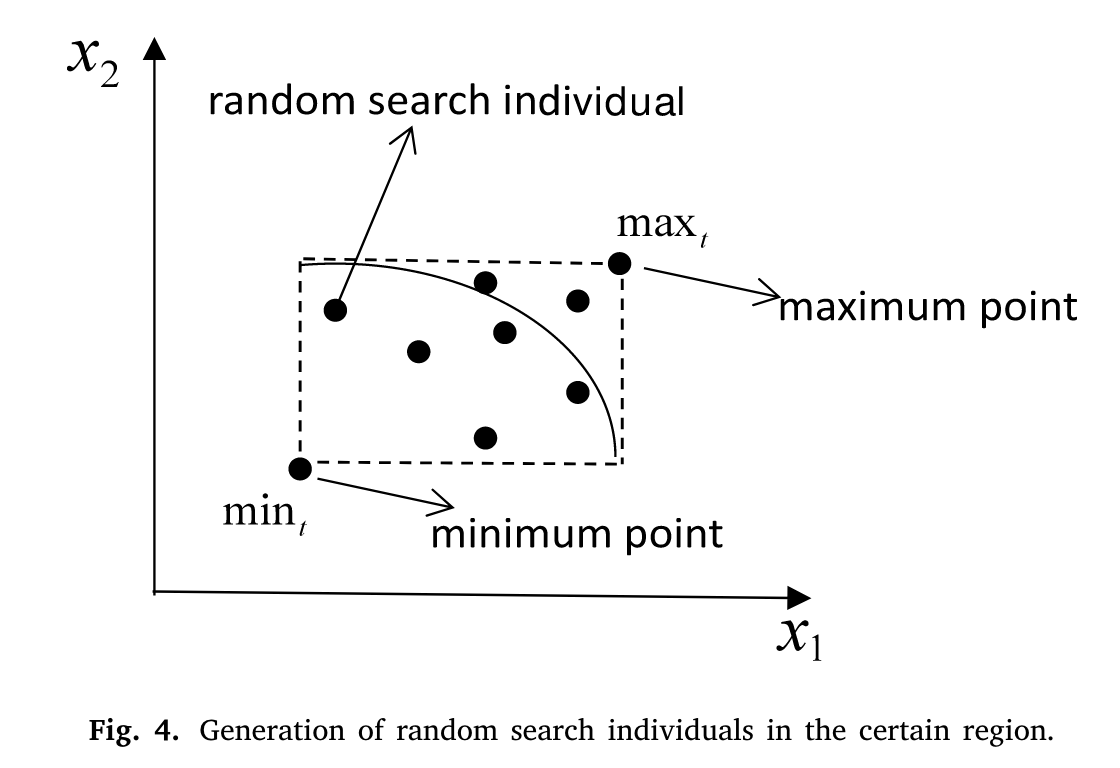
在前两个子种群中,最大点( max )和最小点( min )分别是指决策空间中所有维度目标值最大和最小的个体
个体由![]() 随机生成
随机生成
伪代码如图所示

D.算法整体

伪代码








模拟赛 3 期-大学组(被题目描述坑惨了))
)

)

)
现在更简单了)



)
![[数据湖iceberg]-hive集成数据湖读取数据的正确姿势](http://pic.xiahunao.cn/[数据湖iceberg]-hive集成数据湖读取数据的正确姿势)
