目录
1.数学建模概论
2.生活中的数学建模
2.1.行走步长问题
2.2.雨中行走问题
2.3.抽奖策略
2.4.《非诚勿扰》女生的“最优选择”
3.集体决策模型
3.1.简单多数规则
3.2.Borda数规则
3.3.群体决策模型公理和阿罗定理
1.数学建模概论
1.数学模型的概念
2.数学建模的概念
3.数学建模的一般过程
自然界是按照数学原则设计的，自然界的真正规律必然能够通过数学来探索和表达。
几个数学建模的问题
-
知了鸣叫问题
-
网络犯罪信息的甄别（犯罪克星）
-
树叶形状问题
哥尼斯堡七桥问题
传球游戏问题
1.概率解法：
2.蒙特卡洛解法：
计算机模拟传球N回合，每回合传10次，记录下N回合传球中求最终回到A手中的次数L，则：P=L/N
3.递归解法
设An表示第n次传球后，球在A手中的概率，同样定义Bn，Cn，Dn，En。有传球规则及对称性可知：
Bn = En， Cn = Dn
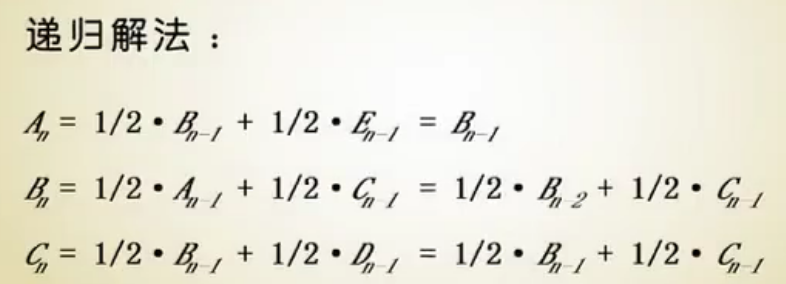
建立模型的大致步骤
-
模型准备
在建模前应该对实际背景又尽可能深入的了解，明确索要解决问题的目的性和要求，手机必要的数据与信息。归纳为一句话：深入了解背景，明确目的要求，收集必要信息。
深入了解背景
明确目的要求
手机必要信息
-
模型假设
充分消化信息
抓住主要因素
做出恰当假设
-
模型建立
用数学语言描述问题
选择适当数学工具
模型要充分简化，以便于求解；同时要保证模型与实际问题有足够的贴近度。
-
模型求解
掌握计算方法
应用数学软件
提高编程能力
MATLAB LINGO等等
-
模型检验
结果检验：将求解结果“翻译”回实际问题中，检验模型的合理性与适用性。
稳定性检验：分析模型对参数变化的“容忍”程度。
敏感度分析：分析目标函数对各变量变化的敏感性。
误差分析：对近似计算结果的误差做出估计。
2.生活中的数学建模
2.1.行走步长问题
设人的质量为M，腿的质量为m，腿长为l，速度为v（固定），单位时间步长为n，步长为x（v=nx）。
单位时间重心升高所需做功为：
腿运动所需的能量
将人行走时腿的运动视为均匀直杆（腿）绕腰部转动，则在单位时间内所需动能为：
动
其中转动惯量
角动量
人行走时单位时间所做的功
势动平平
但是最后计算得到的结果是每秒要走5.4步，每步0.28m，与实际是不符合的。
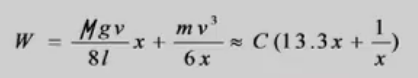
我们进行公式化简发现能量的主要消耗在于势能的消耗上这是不合理的。
有人将腿的转动改为教的直线运动，且将腿的质量全部算到脚上，这样得到的结果大约是每秒3步，是否合理？
2.2.雨中行走问题
问题： 考虑人在雨中沿一直线行走，雨速已知，问人行走的速度多大才能使淋雨量最小？
经过数学推导，总淋雨量目标可以表示为
利用微积分求此函数极值便得到结论：
当0<a<vx时，取u=vx，其他情况下，i应当尽可能大。
建模小结：决定淋雨量大小有两个因素：淋雨时间及单位时间淋雨量，忽略后者将导致错误结论。
2.3.抽奖策略
某人可获得一笔奖金x，x由他在区间[0, 1]中任意地抽取。如果他满意，可以领取x奖金而不再抽取。如果他不满意，可以放弃这个x而重新抽取。这个抽取过程可重复3次，第三次抽取后不得放弃。问他应该采取何种策略以期获得最多奖金？
获奖函数为：
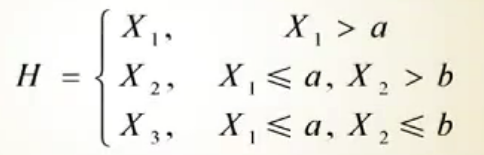
其中X1，X2，X3均为在[0, 1]上均匀分布的随机变量。该人目标为获得的奖金H的期望达最大值。
则H=g(X1, X2, X3)，根据期望计算公式有
令
最大期望奖金为：
最优停止问题。例如“不可召回的秘书招聘问题”。
2.4.《非诚勿扰》女生的“最优选择”
总共面试n人，不选择前k人，从第k+1人起，一旦有比前面更优秀的男生，则选择。
如何确定k。使选到最中意男生的概率最大？对于某个固定的k，能宣导最佳男生的总概率为：
用x来表示k/n的值，并且假设n充分大则上述公式可以近似表示为积分形式：
再对这个式子求导
1/e大约等于37%，即k/n=37%
按此策略，找到最中意男生的概率也是37%
同样的，这个女生空手而归的概率也是37%
3.集体决策模型
根据群体中每个成员的决策结果，综合得出群体的决策结果。两个关键因素：公平性标准、规则。
n个选民：I={1, 2, ..., n}
m哥候选人：A={a1, a2, ..., am}
Pi：选民i对候选人的一个排序
P：根据排序分布{P1, P2, ...., Pn}及选举规则确定的对A中元素群体排序结果。
传递性：对于x，y，z∈A，若x≥y，y≥z，则有x≥z。
三岐性：对一切x，y∈A，必有下列关系之一成立：x＜y x=y x＞y
3.1.简单多数规则
简单多数规则（x＞y）等价于使（x＞y）成立的i的个数大于n/2.
例2
得出一个投票悖论，就是存在最终无法成立的方案。
3.2.Borda数规则
Borda数规则是一种投票计数法，每个选民在选票上对所有候选人进行排序，每个候选人按照不同的排序名次获得相应的Borda数或积分，积分最高的候选人赢得选举。与简单多数规则相比，Borda数规则较不容易选出有争议的人士，但投票结果较容易受策略选举的影响。
在Borda数规则中，每个选民将自己对所有候选人的偏好顺序表达出来，并给予每个候选人相应的得分。例如，如果一个选民最喜欢候选人A，则给A 1分；如果最喜欢候选人B，则给B 2分；如果最喜欢候选人C，则给C 3分；如果最不喜欢候选人D，则给D 4分。这样，每个候选人的得分都会是一个分数和的总和。最终，得分最高的候选人获胜。
与简单多数规则相比，Borda数规则更能够反映出选民的真实偏好顺序，因为它考虑了每个选民对所有候选人的偏好程度。同时，Borda数规则也避免了投票悖论的问题，因为它通过计算每个候选人的总分来确定获胜者，而不是根据单一的简单多数原则来决定胜利者。
然而，Borda数规则也存在一些问题。首先，它需要每个选民对所有候选人进行排序，这需要大量的时间和精力。其次，如果选民的偏好顺序表达不准确，那么可能会导致结果失真。最后，由于计分方法可以产生扭曲的偏好（即无法单纯以一个确定位置偏好的高Borda得票数胜过另一个确定位置偏好的高Borda得票数），所以结果可能受到策略性投票的影响。
策略选举与Borda数规则
例题
设有15个选民与3个候选人x、y、z，有意向表7人 x>y>z：7人 y>x>z：1人 z>x>y B(x)=22，B(y)=21，B(z)=2，所以依据Borda数规则，最后投票结果为x>y>z。
以上称为真诚选举或非策略选举。
3.3.群体决策模型公理和阿罗定理
公理1：（个体选择与群体选择的正相关性）如果对所有i，都有(x＞y)i，那么应当由(x>y)。此性质又称为Pareto效应。
公理2：（无关候选人的独立性）设x，y是任意两个候选人，若在两次投票中，每个选民对x，y的相对排序都不变，那么在两次选举结果中，x，y的相对排序也应不变。
公理3：（非独裁性，Non-dictatorial）不存在这样的选民i，使得(x>y)i推出(x>y)
阿罗定理：对于至少有三名候选人和两名选民的投票，不存在满足阿罗公理的选举规则。
阿罗的结论是：
根本不存在一种能保证效率、尊重个人意向、并且不依赖程序的多数规则的投票方案。或者说不可能通过一定的程序准确地表达社会全体成员的个人意向来达到合意的公共决策。
阿罗的结论是：完美无缺的程序民主不存在！
