一、题记

        最近情绪不太稳定，些许烦躁，也就一直没践行前边说的“学习记录”的想法。现在开始做了，春华易逝，正当时，有想法就去做，踌躇懊悔是这个年纪最不该做的事。

二、前言

        之前说了分块做这个系列，今天就是第一章节——绪论。

---

详情可参考： 数据科学的算法基础——学习记录跳转中心

---

 三、正篇 

        1.数据分析处理阶段

        绪论嘛，以最简练的话讲了几个老步骤：采集、预处理、存储管理、分析挖掘、可视化。大数据学生表示耳朵已经听出茧了，希望可以优化课程尽快先实操。

        2.算法设计原则

        好，有考点——如何对算法进行评价？ 

        （1）效率指标

        耗时少、耗钱少。

        （2）精度指标

                《1》分类问题

混淆矩阵：

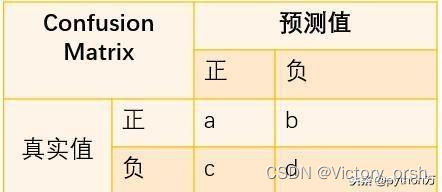
  首先给出四种情况，分别对应图中abcd：

  TP（真阳性）——a      FP（假阳性）——c     TN（真阴性）——d    FN（假阴性）——b

对于称呼有很多不同叫法，我们这里就按教材成为真假、阴阳。

英文名只有一个T——true   F——false   P——positive   N——negative，方便记忆

---

        解释一下：先看预测值（注意看预测值和真实值的位置，这是不固定的），预测值决定P与N，真实值决定T与F：也就是先看预测的，预测的是“正”，哦！那就是阳性的，是真是假呢？看真实值，真是正，那就是真阳性，真实值是负，那就是假阳性（FP）。阴性同理。

         接下来就是用这四个值计算精度指标：

        emmm字丑下次一定注意，实在不想打公式了，而且感觉自己记得更易理解。 

 解释：查全嘛，就是要查得全；查准嘛，就是要查得准。看公式即知。

  最下面一行F值——综合考量查全率和查准率，称为他们的加权调和平均数（通常取1）。

                《2》回归问题

        回归问题主要是进行预测，所以指标较简单：

 平均绝对误差（mean absolute error）：

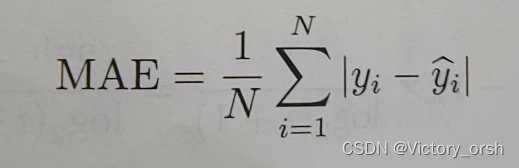
 ———预测值与真实值的绝对误差求和再除以样本个数

 均方误差（mean square error）：

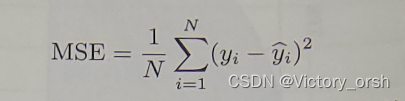
均方根误差（root mean square error）：

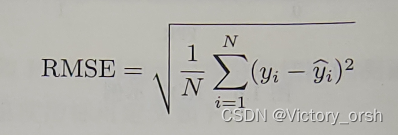
                《3》排序问题 

        同回归类似，也很简单，直接套公式：       

平均精度均值（mean average precision，MAP）：

                                                                              |

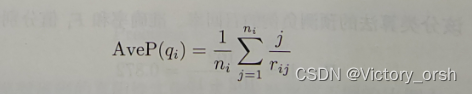
——Q个查询，第i个有n个查询结果，结果的排序为 ，后面有例题

 归一化折损累计增益（normalized discounted cumulative gain，NDCG）：

  

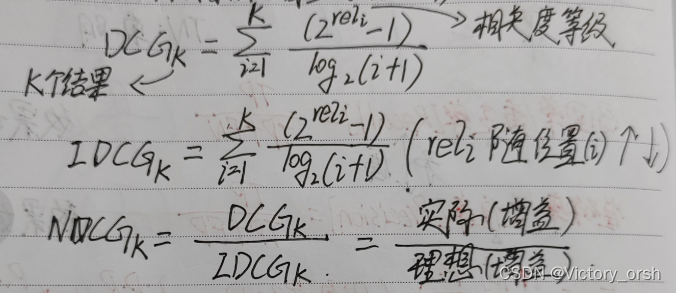
——结合例题理解 

 排序倒数均值（mean reciprocal rank）：

 四、例题

        1.MAP

        假设有两个查询，查询1有4个相关网页，查询2有5个相关网页。检索算法在查询1上检索得到4个相关网页，其排序分别为1，2，4，7；检索算法在查询2上检索得到3个相关网页，其排序分别为1，3，5   试计算该检索算法的平均精度均值。

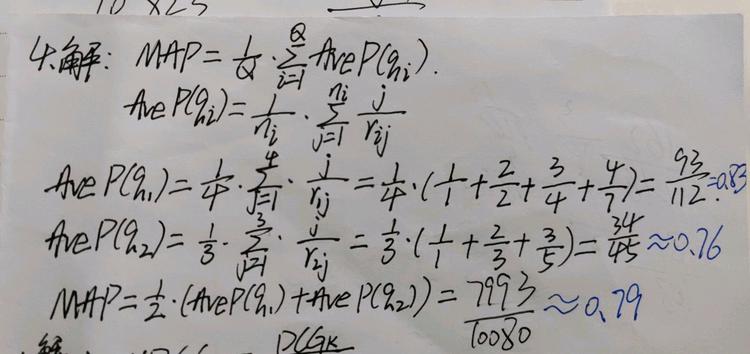
2.MRR

        假设某检索算法响应用户的4个查询，该算法返回4个查询的结果中第一个正确答案的排名分别为1，3，4，2，试计算该检索算法的排序倒数均值。 

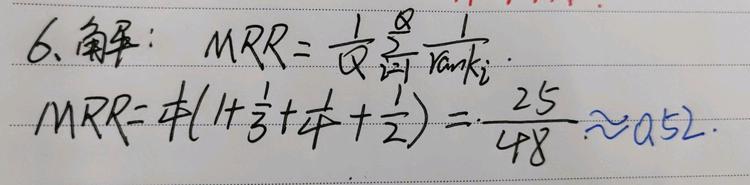
3.NDCG 

假设两个推荐算法推荐Top5产品相关程度依次分别为{3，2，0，1，2}和{2，3，1，2，1}。

（1）分别计算这两个推荐算法的归一化折损累计增益。

（2）基于归一化折损累计增益指标，比较这两个推荐算法的优劣。

只是我写字大，很简单地 

 五、总结

        记公式……

                                                                                                   ————跳转下一章节：抽样算法