1.垂直可视角度
通常使用不同镜头的相机拍摄同一物品的时候,其可以看到的物体的范围是不同的,那么如何表示这一镜头下摄像机所能看到的范围呢?我们定义了一个概念——可视角。如下图所示(两条红线所框出来的角):

实际上当我们定义一个视锥的时候只要定义一个垂直可视角度,一个宽高比,其他信息都能通过这些推理得来。
2.定义屏幕空间
当我们完成mvp操作后(放物体,放相机,投影),我们会获得一个1 * 1 * 1 的小正方体,这时我们得把我们的小正方体转换在二维屏幕上 —— 这样的一个步骤我们称之为光栅化。
屏幕上的最小单位我们称之为像素(前面文章其实提到过,默认单位为1的小正方体),而一个像素的颜色由red , green ,blue 这三元色的不同比例组成。
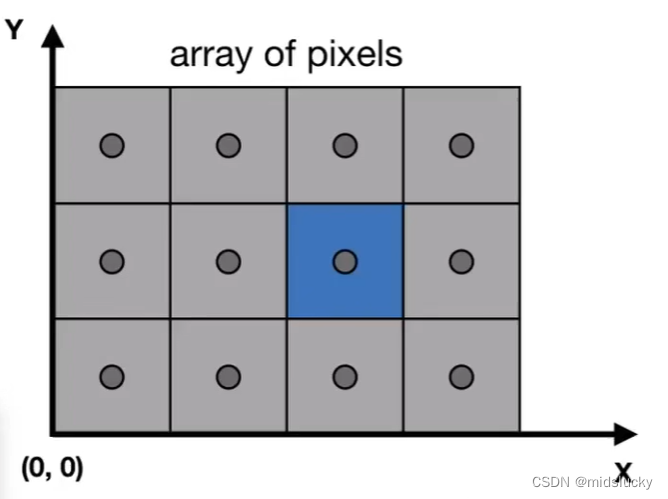
一个像素的坐标默由该小正方体的左下角的点表示,坐标从0开始。
一片像素的表示法:(0,0) to (width-1 , height -1)
一个像素的中心点的坐标为(x+0.5 , y + 0.5)
屏幕整体的覆盖范围(0,0) to (width , height)
那到底如何将立体正方形进行变换到像素空间上呢,我们称这一步为视口变换:
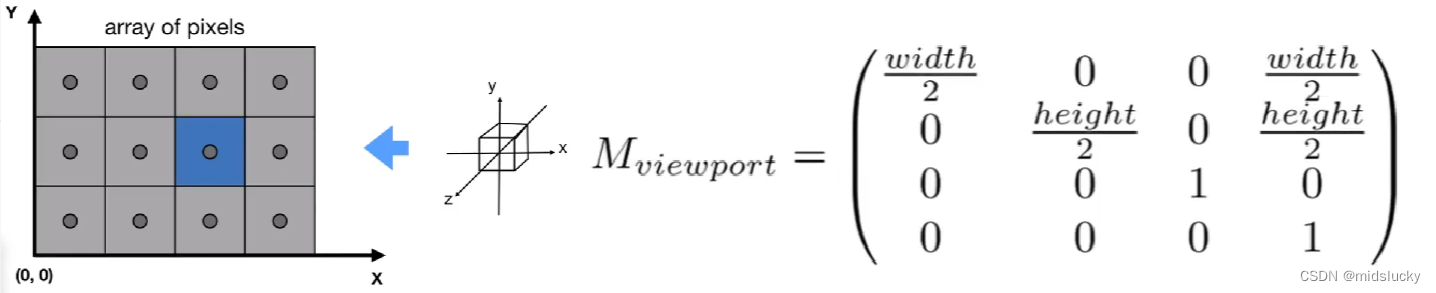
右边的矩阵实际上先做了两部:
1.忽视z坐标,先将立体正方形的中心点变成(0,0),并且长宽与变成了像素覆盖整个屏幕的长宽
2.在将中心点平移到整块像素的中心
这里在给大家介绍一些常见的光栅的显示设备:
LCD(液晶显示器):利用光的波动性,通过液晶造成的扭曲效果改变光的振动方向。
LED(放光二极管):LED的呈像原理就是通过半导体材料的电子结构和能级跃迁,将电能转化为光能,实现发光的效果
3.采样法

通常我们可以用一个又一个的小三角形表示成一个复杂多边形(美术做的工作)。
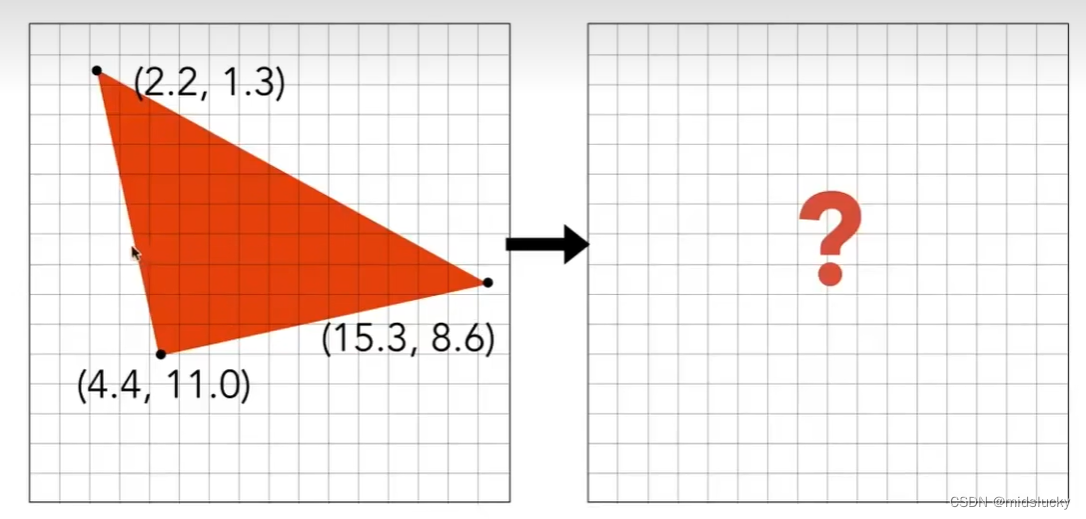
如上图所示,当我们将一个三角形进行实际的屏幕映射时,我们如何判断哪个像素应该染色?
通常我们采用采样法来解决这一问题(当像素的中心点在这个三角形内部中时,我们将其染色)。
(实际上就是一个点是否在一个面内的问题,前面讲过如何处理这一问题)
那万一这一点在三角形边界上又当如何呢?这里就看具体的不同规定了。
这里在给大家科普一个包围盒的概念:
在三维图形学中,包围盒通常是一个立方体,也被称为边界框。***这个立方体完全包含了物体的所有点,使得物体不会超出这个边界框的范围。***这样的包围盒在计算机图形学和游戏开发中经常用于优化碰撞检测、物体的可见性判断、以及加速渲染过程。
4.锯齿问题(走样)
首先我们上面已经说过,我们会用采样发来判断一个个像素的中心是否在三角行内,在的话就染色,但是会导致如下图的问题。

当然采样的不同方法有很多,不仅仅只是我们上面说的那种方式。
类似于锯齿问题的还有摩尔纹,车轮效应。他们的实质是因为采样的速度跟不上信号的变化(这里可以理解成一些图像信息的变化)就会走样。
那么我们究竟该如何防止走样呢?
5.防走样
5.1具体方法的简单描述
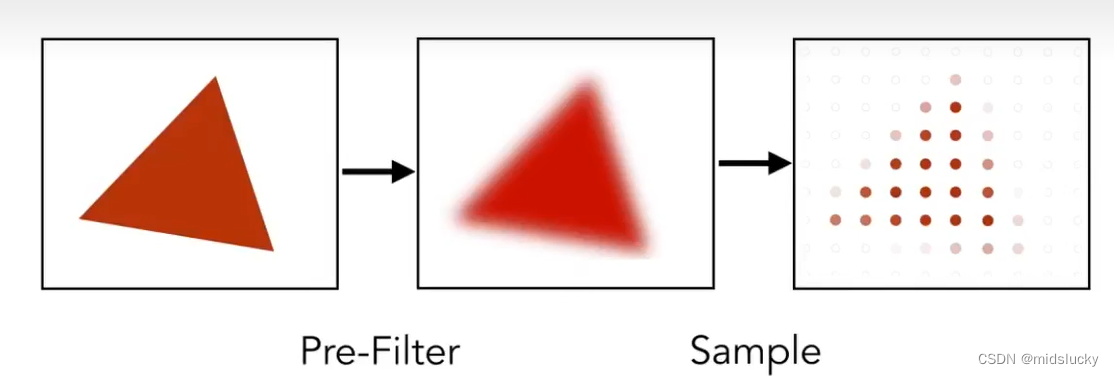
如图所示我们先将上面的三角形进行模糊处理,在采样,具体细节我们会在下文一一道来。
5.2傅里叶变换
傅里叶变换包括傅里叶级数和连续傅里叶变换
首先我们先讲解一下什么是傅里叶级数。
傅里叶级数:一个周期性函数f(t) = 正余弦函数的和
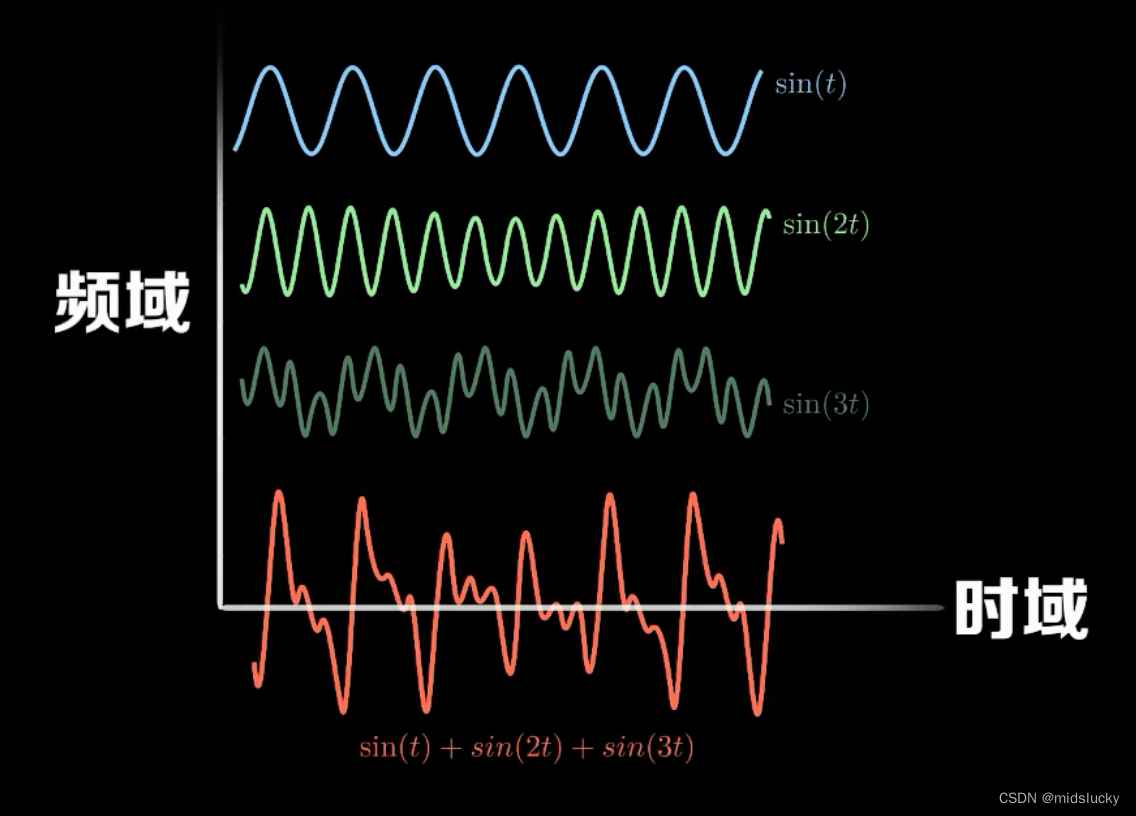
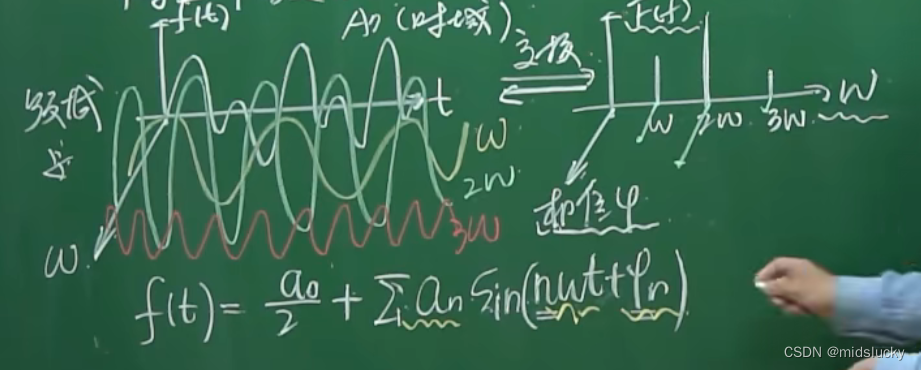
ps:这里的相位代表不同的起始点。
好领悟完上面两幅图后,我们在来说说这个连续傅里叶变换
上面提到了傅里叶级数是用来表示周期性函数的,那么当我们碰到非周期性函数的时候应该怎么办?
这个时候我们的连续傅里叶变换就登场了。

5.3图片的表示方法
我们讲了这么多的傅里叶变换的内容,那么到底和咋们的图形学有什么关系呢?
实际上,对于一张图片来说我们可以使用傅里叶变换将它变成一堆不同频率的波(光的波粒二象性)
具体究竟是个怎么变换法,短时间内很难讲明白,这里先开个坑,不过变换只后的图片的一些特性我们还是能够帮助大家进行一定的分析。

如上这副图,在频域图中,中心为低频区域,而我们的四周为高频区域,亮度表示图像信息的多少,比如上面一幅图,图像的信息大多集中在低频上。
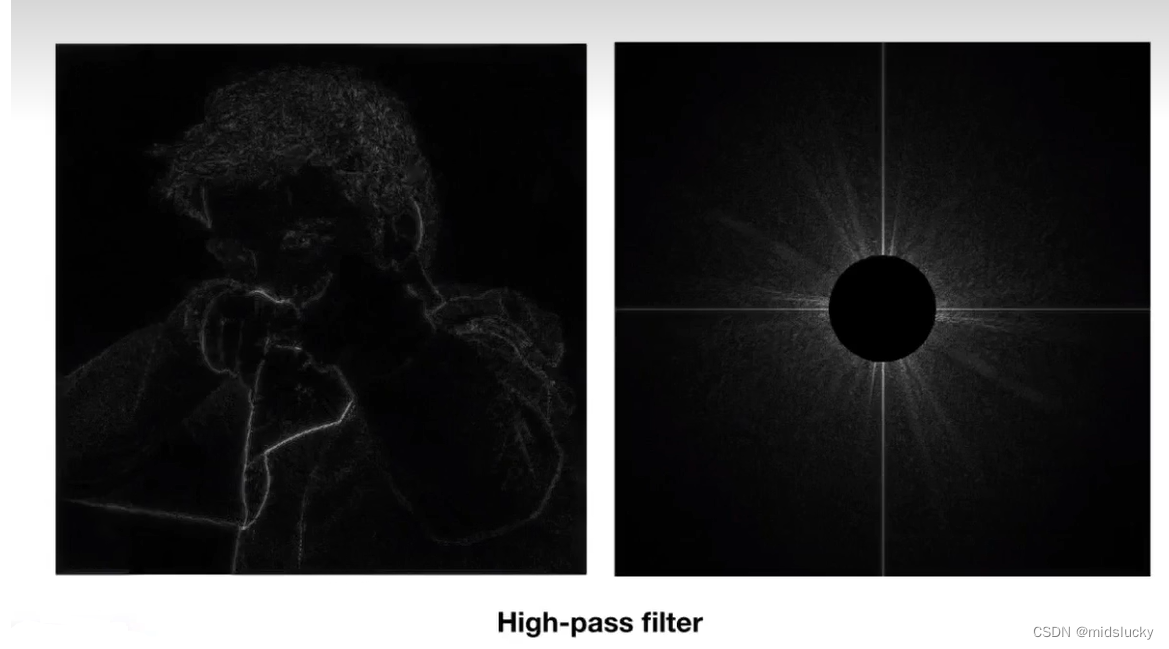
之后我们采样高通滤波器,将我们低频的信息过滤掉,就变成了如上图这样。
实际上这里的高频描述的是图片中人物的边框,为什么呢?拿上面这个哥们的衣服举例,其褶皱度比较大,凹凸不平,一般这样的图片部分所代表的往往是我们的高频信息。

接着我们采用低通滤波器得到了这样的一幅图。实际上我们看到低频信息是一副图的大致整体部分,一些凹凸,轮廓感这样的细节信息全部去掉了。
5.4卷积操作
好那么终于要开始要讲解我们的防走样方法了(就是上面提到的模糊处理)。
这里我们先来介绍一下我们的卷积操作:
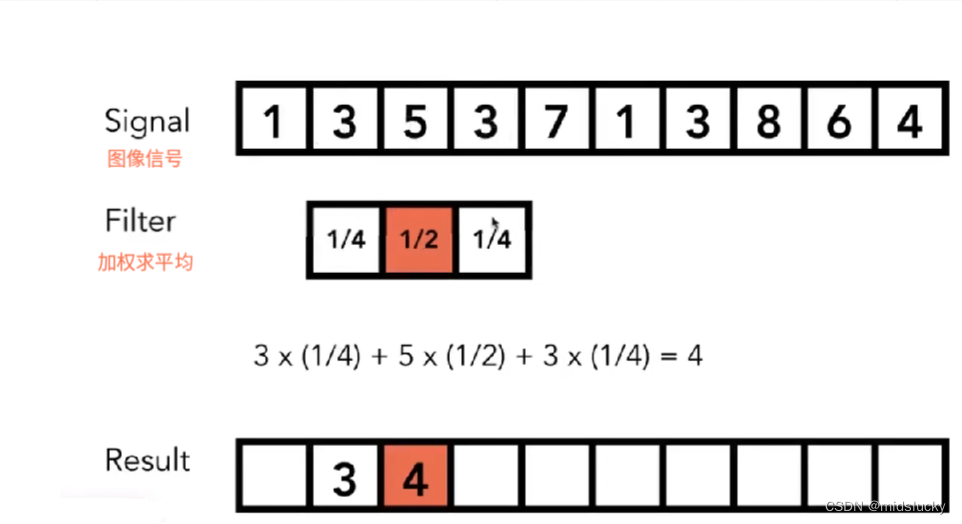
那么用到实际图像处理上是什么样的呢?
如下图所示:
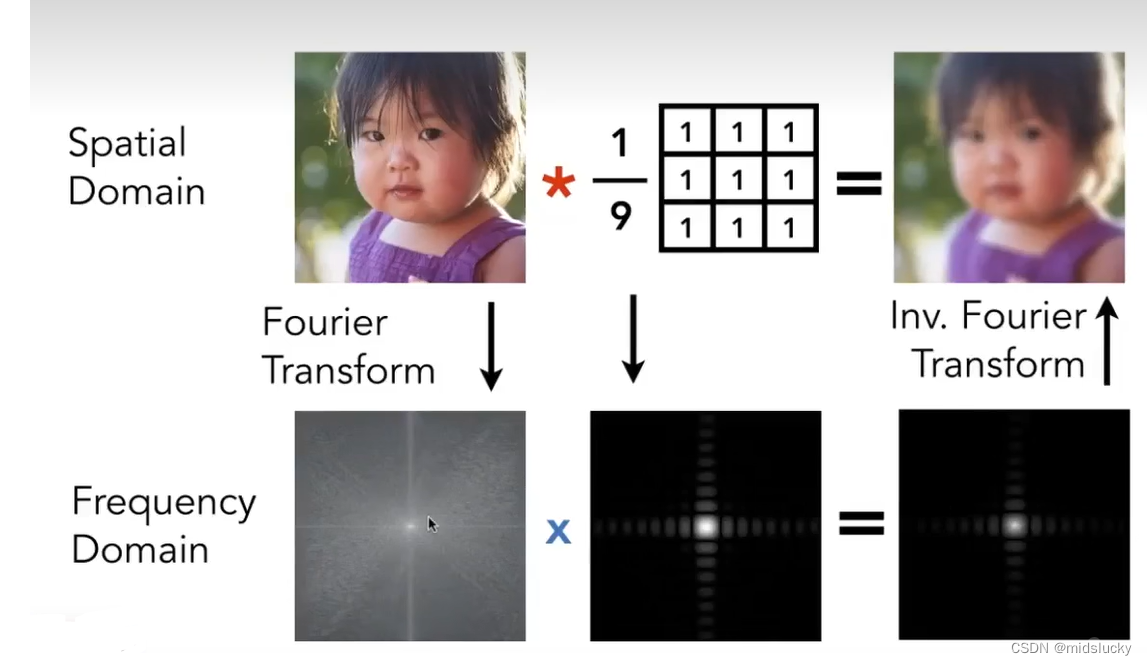
这副图的上半部分是在时域上面进行处理的一个抽象图,对于该图片上任何一个像素,我们取它周围的3乘以3的这样的一块像素空间,求信号的评价数值然后再写回去,就会得到这样的一副模糊的图片。
这副图片的下半部分就是我们再图片转换为频域后进行一个类似于运用录波器原理的这样的一个处理方式。
5.5从本质上来理解走样现象
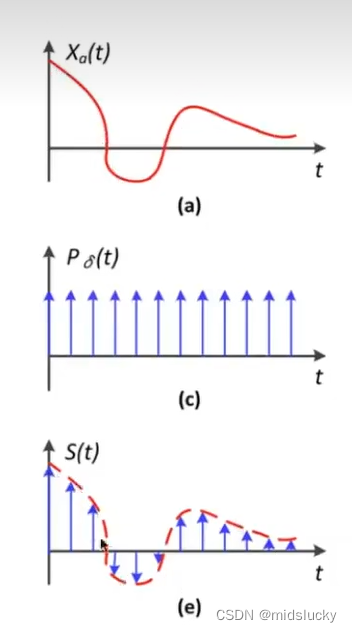
上图是一段在时域当中的频率变换图,我们采样的操作实际就是冲击函数和最开始的频率图相互结合,然后生成了如e这样一段段离散化的频率图来代表我们当前图片的一些频率信息。
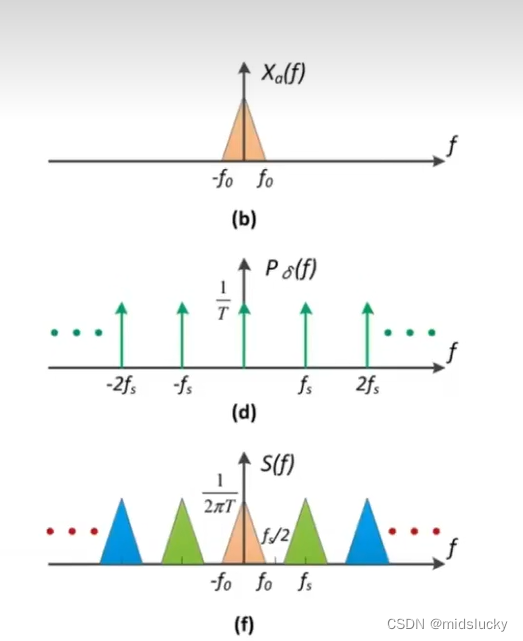
上图是相对于的频域的处理,可以看到的是,采样的实际操作在频域上的表现是在将原本的频谱(就是图b)复制粘贴了很多份。
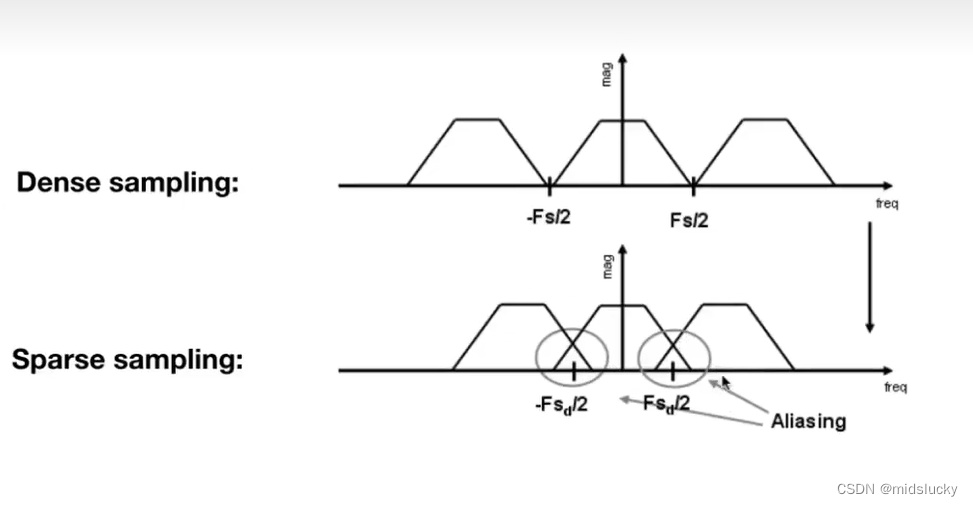
实际上,当我们的采样的速度不快,采样率比较稀疏的时候,所对应的频谱就会显示上图这样的情况,频谱在搬移的情况下发生了混叠,导致了走样。
总结一下走样的本质是由于采样率不足,未能准确捕捉信号变化(换个说法信号变换的太快了),导致信号失真。
5.6反走样方法的总结
1.增加采样率
2.先模糊(将高频信息砍掉)在采样
5.7MSAA方法
当然实际防走样我们肯定不能像上面进行这个复杂的操作,我们还是采样一种近似的方法来处理我们的走样,这里给大家介绍一种常用的方法MSAA。
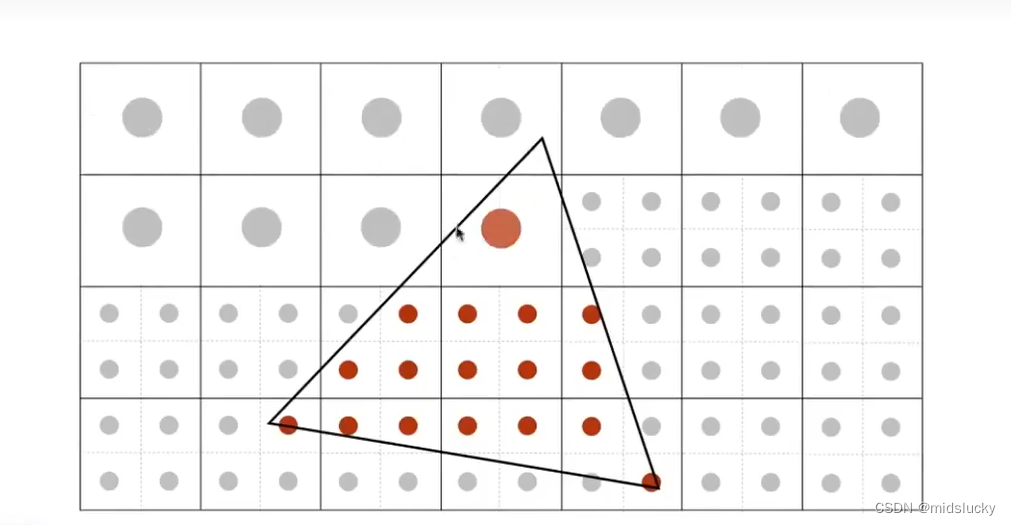
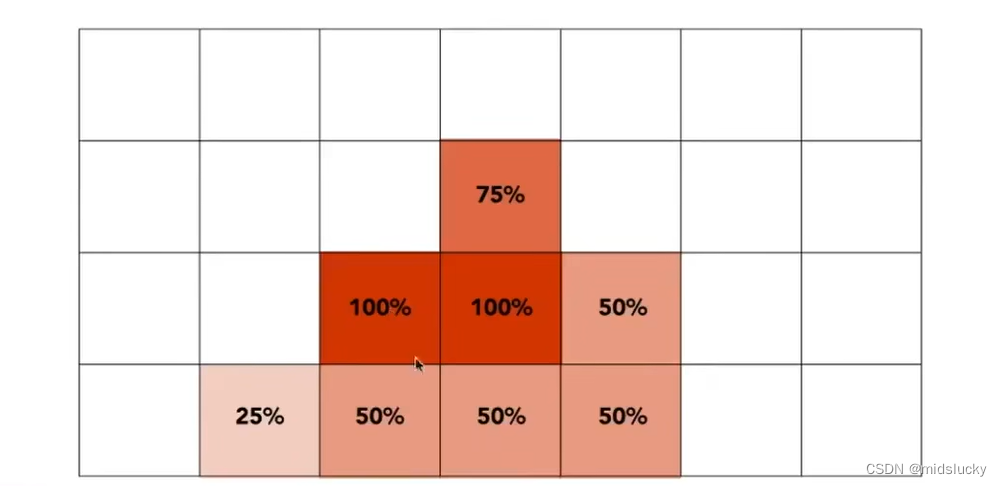
实际上就是把一个像素在多分几块区域,然后看三角形单个像素内不同区域的覆盖情况,根据这一情况改变颜色的深度。
当然这么做会增大计算量,导致性能的消耗。
实际在单个像素的区域划分上也是有讲究的,不会像上图那样平均划分。
下面给大家在介绍一些其他常用的抗锯齿方案:
1.FXAA(fast approximate aa) 先得到一个有锯齿的图,然后找到边界进行一些替换操作
2.TAA(temporal AA) 复用上一帧的数值
还有一个有意思的技术在这里也跟大家科普一下:
超分辨率技术:当想提高一张图的分辨率时,本质上来将就是将一张拉大然后补充细节,而我我们并不知道其中的细节是什么,这个时候就需要进行一些猜测,而我们的DLSS(深度学习)技术就很适合做一些类似的工作。


















与拼接火车(应用)厢的乐趣)
