实验四:动态规划
实验目的
• 理解动态规划的基本思想,理解动态规划算法的两个基本要素最 优子结构性质和子问题的重叠性质。
• 熟练掌握典型的动态规划问题。
• 掌握动态规划思想分析问题的一般方法,对较简单的问题能正确 分析,设计出动态规划算法,并能快速编程实现。
钢条切割问题
有一段长度为n的钢条,钢条可以被分割成不同的长度的小钢 条出售,不同的小钢条对应不同的售价。详见下表:
| 钢条长度 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
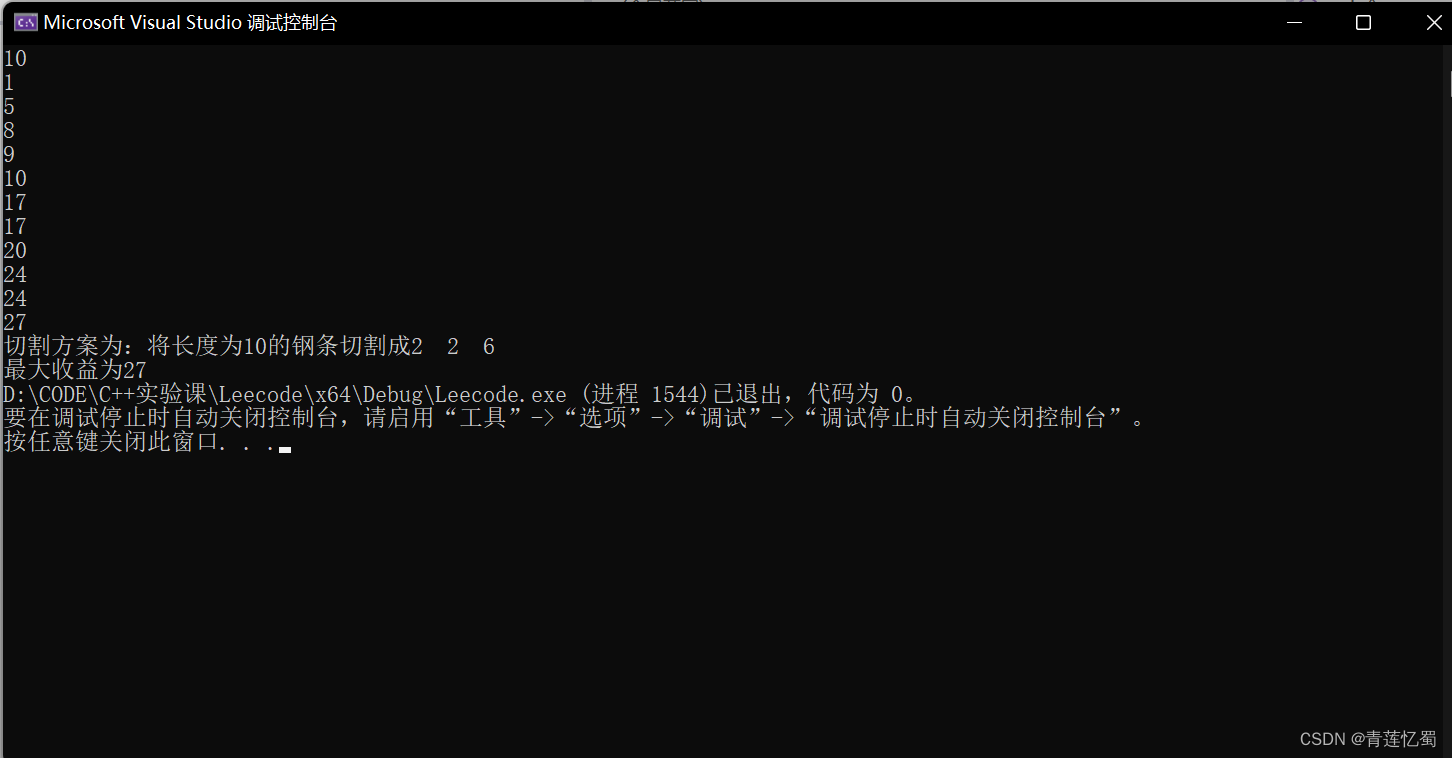
| 价格p | 0 | 1 | 5 | 8 | 9 | 10 | 17 | 17 | 20 | 24 | 24 |
钢条切割问题是这样的: 给定⼀段长度为n的钢条和⼀个价格表 pi(i=1,2,…n), 求切割钢条⽅案, 使得销售收益最⼤。 注意, 如果长度为n英⼨的钢条的价格pn⾜够⼤, 最优解可能就是完全不需 要切割。
输入:钢条的长度n,不同长度钢条的价值Pi,{i=1,…,n}
输入:1、最大收益,2、切割方案。
问题分析
我们选用一个状态方程去描述问题,设f(i,j)为状态方程,含义是在0~i种可被切割长度,j为当前钢条长度,举例f(3,5)意思就是在当前长度为5的时候,钢条可被切成0,1,2,3,这几种长度。
当我们不选择第i种切割方式时,那么还剩i-1种切割方式,所以有状态转移方程
f ( i , j ) = f ( i − 1 , j ) f( i,j)=f(i-1,j) f(i,j)=f(i−1,j)
当我们选择第i种切割方式的时候,如果此时 i > j i>j i>j, 那么应该放弃这种方案,即状态转移方程为
f ( i , j ) = f ( i − 1 , j ) f(i,j)=f(i-1,j) f(i,j)=f(i−1,j)
如果此时 i < = j i<=j i<=j, 因为这种方式可能被选择多次,所以我们选择k次来表示,以不失一般性,那么状态转移方程为
f ( i , j ) = m a x ( ∑ k = 0 + ∞ f ( i − 1 , j − k ∗ i ) + k ∗ a [ i ] ) f(i,j)=max(\sum_{k=0}^{+\infty}f(i-1,j-k*i)+k*a[i]) f(i,j)=max(k=0∑+∞f(i−1,j−k∗i)+k∗a[i])
然后将选择第i种方案合并,即状态转移方程为
f ( i , j ) = m a x ( f ( i − 1 , j ) , ∑ k = 0 + ∞ f ( i − 1 , j − k ∗ i ) + k ∗ a [ i ] ) f(i,j)=max(f(i-1,j), \ \sum_{k=0}^{+\infty}f(i-1,j-k*i)+k*a[i]) f(i,j)=max(f(i−1,j), k=0∑+∞f(i−1,j−k∗i)+k∗a[i])
这里我们进行一个数学方程的变换
f ( i , j − i ) = m a x ( ∑ k = 0 + ∞ f ( i − 1 , j − ( k + 1 ) ∗ i ) + k ∗ a [ i ] ) f(i,j-i)=max(\sum_{k=0}^{+\infty}f(i-1,j-(k+1)*i)+k*a[i]) f(i,j−i)=max(k=0∑+∞f(i−1,j−(k+1)∗i)+k∗a[i])
可以将两个式子联立
f ( i , j ) = m a x ( f ( i − 1 , j ) , f ( i , j − i ) + a [ i ] ) f(i,j)=max(f(i-1,j),\ f(i,j-i)+a[i]) f(i,j)=max(f(i−1,j), f(i,j−i)+a[i])
分析完毕
源代码
#include <iostream>
using namespace std;int a[1000];
int dp[1000][1000];
int x[1000];int fun(int len) {for (int i = 1; i <=len; i++) {for (int j = 0; j <=len; j++) {dp[i][j]=dp[i-1][j];if(j>=i)dp[i][j] = max(dp[i-1][j], dp[i][j - i] + a[i]);}}return dp[len][len];
}void traceback(int j, int y)
{while (j) {while (y < j) {j--;}if (dp[j][y] == (dp[j][y - j] + a[j])) {x[j]++;y = y - j;++j;}j--;}
}
int main(){int len = 0;int sum = 0;bool flag=1;cin >> len;for (int i = 1; i <= len; i++) {scanf("%d", &a[i]);}cout << fun(len)<<endl;traceback(len, len);cout << "切割方案为:将长度为" << len << "的钢条切割成";for (int i = 1; i <= len; i++) {while (x[i]--) {cout << i << " ";sum = sum + a[i];}}cout << "\n最大收益为" << sum;return 0;
}
然后可以优化代码,让空间复杂度减小一倍
int a[1000];
int dp[1000];
int x[1000];int fun(int len) {for (int i = 1; i <=len; i++) {for (int j =i; j <=len; j++) {dp[j] = max(dp[j], dp[j - i] + a[i]);}}return dp[len];
}void traceback(int j, int y)
{while (j) {while (y < j) {j--;}if (dp[y] == (dp[y - j] + a[j])) {x[j]++;y = y - j;++j;}j--;}
}
int main(){int len = 0;int sum = 0;bool flag=1;cin >> len;for (int i = 1; i <= len; i++) {scanf("%d", &a[i]);}cout << fun(len)<<endl;traceback(len, len);cout << "切割方案为:将长度为" << len << "的钢条切割成";for (int i = 1; i <= len; i++) {while (x[i]--) {cout << i << " ";sum = sum + a[i];}}cout << "\n最大收益为" << sum;return 0;
}
结果演示
实验总结
在写这个实验的时候,刚开始我使用了递归的方法,然后由于递归比较难回溯,所以改进算法,使用了动态规划,这道题我研究调试代码很长时间,虽然耗费很久,但是通过这次实验我对动态规划掌握更进一步,还是让我受益良多。当面对一些具有重叠子问题性质的问题时,动态规划(Dynamic Programming)是一种常用的解决方法。它通过将问题拆分为更小的子问题,并将子问题的解存储起来,避免了重复计算,从而提高算法的效率。动态规划的基本思想是利用已经计算过的子问题的解来计算更大规模的问题的解,这种思想被称为"最优子结构"。通过定义状态、状态转移方程和初始条件,我们可以构建动态规划算法。动态规划可以分为以下几个步骤:定义状态:明确问题需要求解的状态是什么,可以用一个或多个变量来表示。这些状态可以表示问题的规模、位置、限制条件等。确定状态转移方程:找到问题的递推关系,即将大规模问题的解表示为小规模问题的解。这需要根据问题的特点和已知信息建立数学模型。状态转移方程描述了问题从一个状态转移到另一个状态的方式。定义初始条件:确定最小规模的问题的解,即边界条件。这些初始条件可以是已知的问题解,或者根据问题的特点进行定义。使用迭代或递归的方式计算问题的解:根据状态转移方程,使用循环迭代或递归方式计算问题的解,并将中间结果保存起来,避免重复计算。输出结果:根据问题要求,输出最终求解得到的结果。动态规划在解决一些经典问题中非常有效,如背包问题、最长公共子序列问题、最短路径问题等。通过合理定义状态和状态转移方程,动态规划可以大大简化问题的求解过程,提高算法的效率。




)

![[2023年]-hadoop面试真题(一)](http://pic.xiahunao.cn/[2023年]-hadoop面试真题(一))





、call()、apply()( 含手写 bind,手写 call,手写 apply ))






