一：题目
二：思路分析
2.1 蛇形矩阵含义
首先，这道题我们要根据这个示例，找到蛇形矩阵是怎么移动的
这是，我们可以标记一下每次移动到方向
我们根据上图可以看出，蛇形矩阵一共有两种方向，橙色的是斜向右上角，蓝色的是斜向左上角，根据这个图的最后一个的点（16），我们可以先补出一个红色三角形，再根据这个三角形，可以补充为一个矩形。
而这个三角形中，经过最后一个数据16的是第七行，所以循环时最后的条件是小于等于7（2*n-1）
2.2一种方向
蛇形矩阵一有两种方向，我们可以把问题简单化，先求只按照一个方向排，如何计算？
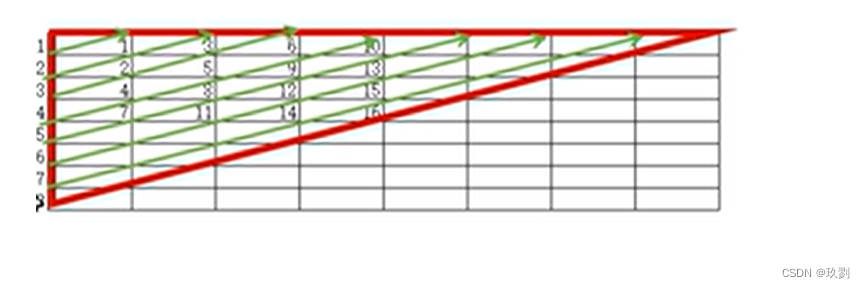
如果所有数字按照斜向右递增，如何写代码呢?
首先每次开始排序的都是每一行的第一列，让后向上递增就是行变小，列变大。
#include <stdio.h>int main() {int n = 0;scanf("%d",&n);int arr[1005][1005] = {0};int i = 0;int cont = 1;for(i = 1; i<=2*n-1;i++){int x = i;//行int y = 1;//列while(x >= 1){//在n*n矩阵中才会赋值if(x <= n&& y <=n){arr[x][y] = cont++;}y++;x--;}}for(i =1;i<=n;i++){for(int j = 1; j<=n;j++){printf("%d ",arr[i][j]);}printf("\n");}return 0;
}2.3第二种方向就是行列互换
完成上述代码时，我们的蛇形矩阵已经完成一半了，另一半的矩阵顺序是反着的
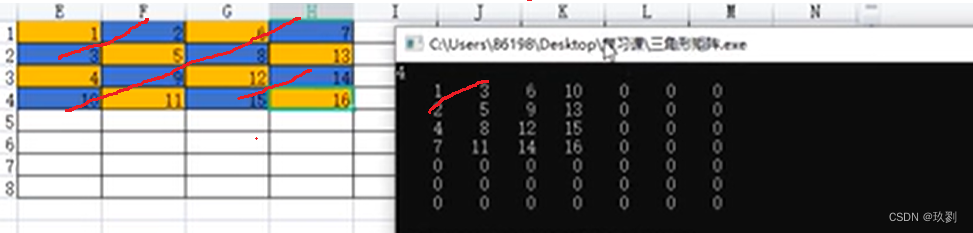
而且，仔细看反着的顺序就是将我们所打印的数字行列进行互换即可，而且顺序不一致的都死偶数列
三：代码
#include <stdio.h>int main() {int n = 0;scanf("%d",&n);int arr[1005][1005] = {0};int i = 0;int cont = 1;for(i = 1; i<=2*n-1;i++){int x = i;//行int y = 1;//列while(x >= 1){//在n*n矩阵中才会赋值if(x <= n&& y <=n){if(i%2 != 0){//奇数行就是顺序arr[x][y] = cont++;}else {arr[y][x] = cont++;} }y++;x--;}}for(i =1;i<=n;i++){for(int j = 1; j<=n;j++){printf("%d ",arr[i][j]);}printf("\n");}return 0;
}
)
