一、几何变换

7.图像的插值

(1)原理介绍

下面对比三种插值方法，分别是最近邻插值法、双线性插值法、卷积插值法，三种方法的前提和特点、优缺点、适用场景如下：

1. 最近邻插值（Nearest Neighbor Interpolation）：

   • 前提与特点：这是最简单的插值方法，不考虑相邻像素的影响，只取最近的像素值。对于每个新像素点，此方法找到最近的原始输入像素点并直接赋予其灰度值。
   • 优点：计算速度快，没有引入新的颜色（对于彩色图像），在某些应用中保留了像素的原始值。
   • 缺点：图像质量通常不是最优的，可能会出现锯齿状边缘和像素化的效果，特别是在放大较大比例时。
   • 适用场景：适用于需要实时处理的场景，或者当图像放大倍数较小，对图像细节要求不高时。

2. 双线性插值（Bilinear Interpolation）：

   • 前提与特点：此方法考虑了像素周围的2x2邻域，通过线性插值算法基于周围四个最近的像素点，对于新的像素点进行灰度值的估算。
   • 优点：比最近邻插值算法图像质量更好，可以得到更加平滑的图像边缘，没有那么明显的锯齿、像素化现象。
   • 缺点：相比于最近邻插值，双线性插值计算量更大，处理速度稍慢。
   • 适用场景：适用于图像质量要求较高的场合，同时可以接受一定程度的模糊。

3. 双立方插值（Bicubic Interpolation）：

   • 前提与特点：此方法使用像素周围的4x4邻域进行插值，是一种更为复杂的算法，通过多项式插值，对图像中的像素值进行估算。
   • 优点：相比于最近邻和双线性插值，双立方插值通常可以得到更平滑、边缘更少锯齿的图像，并且在保留更多图像细节方面更为出色。
   • 缺点：计算量大，处理速度较慢，可能会引入一些伪影。
   • 适用场景：适合对图像质量要求非常高的应用，比如专业的图像编辑和打印。

(2)完整代码

import cv2
import numpy as np
import matplotlib.pyplot as plt# 读取图片并转换为灰度图
image = cv2.imread('cell.jpg', cv2.IMREAD_GRAYSCALE)# 确保图片大小为224x234
if image.shape != (234, 224):image = cv2.resize(image, (224, 234), interpolation=cv2.INTER_LINEAR)# 最近邻插值法
nearest = cv2.resize(image, (448, 468), interpolation=cv2.INTER_NEAREST)# 双线性插值法
bilinear = cv2.resize(image, (448, 468), interpolation=cv2.INTER_LINEAR)# 双立方插值法（卷积插值法通常指的是双立方插值）
bicubic = cv2.resize(image, (448, 468), interpolation=cv2.INTER_CUBIC)# 创建一个横排的子图，显示三种不同的插值结果
fig, axes = plt.subplots(nrows=1, ncols=3, figsize=(15, 5))# 设置每个子图的标题
axes[0].set_title('Nearest Neighbour')
axes[1].set_title('Bilinear')
axes[2].set_title('Bicubic')# 在子图中显示对应的插值结果图像
axes[0].imshow(nearest, cmap='gray')
axes[1].imshow(bilinear, cmap='gray')
axes[2].imshow(bicubic, cmap='gray')# 关闭子图各自的坐标轴
for ax in axes:ax.axis('off')# 调整子图之间的间隔
plt.subplots_adjust(wspace=0.05, hspace=0)# 显示图像
plt.show()

(3)运行结果

二、离散傅里叶变换

(1)原理介绍

1)原理：

在二维图像中，DFT将图像从空间域（其中每个像素位置表示一个点的亮度或颜色强度）转换到频域（其中每个点表示一个特定频率和方向上的信号强度）。这个频域表示让我们能够观察到图像中的周期性和非周期性模式。

图像的DFT生成复数输出，其中实部代表余弦（cosine）波的幅度，虚部代表正弦（sine）波的幅度。图像中的每一个点都可以看作是许多不同频率和方向的正弦和余弦波的叠加。

2)适用场景：

1. 频域滤波：在频域中，可以对图像进行低通、高通和带通滤波等操作，用于平滑图像（去噪）或增强边缘等。

2. 图像分析：通过分析图像的频域表示，可以识别图像中的周期性模式、分析纹理或者进行图像压缩。

3. 图像增强：一些图像增强的技术，如锐化或对比度增强，也可以通过调整图像的频域成分来实现。

4. 图像重建：利用逆傅里叶变换可以重建图像，这在图像压缩和传输中非常有用。

5. 水印和隐写术：嵌入信息或水印到图像的特定频率成分中，这样在空间域中这些信息几乎是不可见的。

6. 特征提取：在计算机视觉和图像处理中，频域特征可以用于图像识别和分类。

3)注意事项：

• 离散傅里叶变换对于数据的周期性和非周期性特征都非常敏感，因此在应用DFT之前通常需要对图像边缘进行处理，如使用窗函数，以减少边界效应。
• DFT变换后的图像一般将低频部分放在图像中心，因为在自然图像中，高频通常代表着边缘和噪声，而低频则对应于图像的整体构成。

(2)完整代码

import numpy as np
import matplotlib.pyplot as plt
import cv2# 读取图像
image = cv2.imread('cell.jpg', cv2.IMREAD_GRAYSCALE)# 检查图像是否正确读取
if image is None:raise ValueError("Could not open or find the image. Check the path.")# 对图像进行离散傅里叶变换
dft = np.fft.fft2(image)
# 将DFT输出中的低频成分移动到数组的中心
dft_shifted = np.fft.fftshift(dft)
# 计算幅度谱
magnitude_spectrum = 20 * np.log(np.abs(dft_shifted))# 创建一个横排的显示图像和频域图像的新图
plt.figure(figsize=(12, 6))# 显示原始图像
plt.subplot(1, 2, 1) # (rows, columns, panel number)
plt.imshow(image, cmap='gray')
plt.title('Original Image')
plt.axis('off')# 显示频域图像
plt.subplot(1, 2, 2)
plt.imshow(magnitude_spectrum, cmap='gray')
plt.title('Magnitude Spectrum')
plt.axis('off')# 显示图像
plt.tight_layout() # 调整子图，使之填充整个图像区域
plt.show()

(3)运行结果

(4)与沃尔什-哈达玛变换（WHT）和离散余弦变换（DCT）的对比

        说到DFT，有的教材就会提到另外两种频域变换方法：沃尔什-哈达玛变换（WHT）和离散余弦变换（DCT），三者最主要的区别就是：WHT最快，并且对二值化图像处理效果最好，但图片尺寸必须2的幂(或你愿意预处理成2的幂)；DCT常用于JPEG图像的图像压缩，但不涉及复数运算；DFT慢一点，但是常用于滤波、去噪、复原。详细的对比如下：

1. 离散傅里叶变换（DFT）

适用场景：

• 频域分析：如果您需要分析图像中的频率成分，例如确定图像的纹理信息或频率特征，DFT是理想的选择。
• 频域滤波：如果您的目的是移除图像中的噪声（通常在高频区域）或强调某些纹理（低频信息），使用DFT之后可以应用各种频域滤波器。
• 图像去噪：通过DFT，可以设计滤波器来抑制噪声频率，然后通过逆变换恢复图像。
• 图像复原：在图像复原中，通过频域分析可以识别并补偿成像系统的模糊函数。

选择条件：

• 需要分析或处理图像的频率内容。
• 计算复杂度不是主要关心的问题，或者可以接受稍长的计算时间。

2. 沃尔什-哈达玛变换（WHT）

适用场景：

• 快速计算：当需要非常高效的计算时，WHT由于其简单的+1和-1操作，可以比DFT或DCT更快地实现。
• 二值图像：对于二值图像或其他只有两种值的图像，WHT可能尤其有用。
• 数据加密和水印：WHT可用于快速加密信息或嵌入水印，因为它对图像的局部变化不敏感。

选择条件：

• 计算效率是优先考虑的问题，特别是对于实时系统。
• 图像尺寸必须是2的幂，或者您愿意对图像进行相应的预处理。

3. 离散余弦变换（DCT）

适用场景：

• 图像压缩：DCT在JPEG图像压缩中非常常用，它能够将图像能量集中在较少的系数中，使得压缩效率高。
• 去噪：类似于DFT，DCT也可以用于图像去噪，但通常更有效，因为实际图像的能量大多集中在DCT的低频系数中。
• 图像增强：如果要增强图像的某些特征，DCT可以帮助分离出重要的频率成分并进行处理。

选择条件：

• 对图像执行压缩或需要高效的能量集中变换。
• 对实数操作有偏好，因为DCT不涉及复数计算。

4.完整代码

import numpy as np
import matplotlib.pyplot as plt
import cv2
from scipy.fftpack import dct, idct
from scipy.linalg import hadamard# 读取图像
image = cv2.imread('cell.jpg', cv2.IMREAD_GRAYSCALE)# 检查图像是否正确读取
if image is None:raise ValueError("Could not open or find the image. Check the path.")# 离散傅里叶变换 (DFT)
dft = np.fft.fft2(image)
dft_shift = np.fft.fftshift(dft)  # 将低频分量移动到中心
dft_magnitude = np.log(np.abs(dft_shift))# 离散余弦变换 (DCT)
dct_transformed = dct(dct(image.T, norm='ortho').T, norm='ortho')# 沃尔什-哈达玛变换 (WHT)
# 由于WHT需要尺寸为2的幂，因此可能需要调整图像尺寸
dim = 2 ** int(np.ceil(np.log2(max(image.shape))))
padded_image = np.pad(image, ((0, dim - image.shape[0]), (0, dim - image.shape[1])), 'constant', constant_values=0)
hadamard_transformed = hadamard(dim)
wht_transformed = hadamard_transformed @ padded_image @ hadamard_transformed
wht_magnitude = np.log(np.abs(wht_transformed))# 显示图像
plt.figure(figsize=(18, 6))# 显示DFT
plt.subplot(1, 3, 1)
plt.imshow(dft_magnitude, cmap='gray')
plt.title('Discrete Fourier Transform')
plt.axis('off')# 显示DCT
plt.subplot(1, 3, 2)
plt.imshow(dct_transformed, cmap='gray')
plt.title('Discrete Cosine Transform')
plt.axis('off')# 显示WHT
plt.subplot(1, 3, 3)
plt.imshow(wht_magnitude, cmap='gray')
plt.title('Walsh-Hadamard Transform')
plt.axis('off')plt.tight_layout()
plt.show()

5.运行结果

6.方法选择

假设您有一张照片，您需要根据照片的特点和您要实现的功能来确定使用哪种方法。以下是一些指导性的问题：

1. 您的目标是什么？

   • 如果您需要压缩或者进行简单的频域去噪，DCT可能是最佳选择。
   • 如果是进行深入的频域分析或者复杂的频域滤波，DFT可能更合适。
   • 如果需要快速变换或者数据加密，并且图像大小合适，WHT可能是一个好的选择。

2. 图像的特性是什么？

   • 对于典型的自然图像，DCT通常是最有效的，因为它能够集中图像能量。
   • 对于含有大量细节或者高频信息的图像，DFT可能会提供更多的信息。
   • 对于二值图像或者图像尺寸已经是2的幂的情况，WHT可能更有优势。

3. 计算效率要求如何？

   • 如果需要快速处理，WHT可能是最快的，尤其是在尺寸合适的情况下。
   • 如果效率不是主要关心点，那么DFT和DCT都是可行的，具体取决于上述的其他因素。

三、图像增强

1.对比度增强

(1)灰度线性变换与灰度分段线性变换

1)原理介绍

灰度线性变换

原理： 灰度线性变换涉及将图像的每一个像素值按照一个简单的规则进行调整，这个规则会让所有像素变得更亮或更暗，并且可以改变图像的对比度。换句话说，这种变换就像调整电视或者显示器的亮度和对比度控制钮。

使用场景：

• 当整张图像看起来太暗或者太亮时，可以通过灰度线性变换来统一调整图像的亮度。
• 当整个图像的对比度不够，显得很平淡无力时，可以通过这种变换来提高对比度，使得图像中的明暗部分更加突出。

灰度分段线性变换

原理： 灰度分段线性变换比灰度线性变换复杂一些，它允许你对图像中不同亮度区域进行不同方式的调整。这意味着你可以选择只提亮图像中的暗部分，而保持亮部分不变，或者反过来，也可以对亮度中等的区域进行调整，而不影响其他区域。

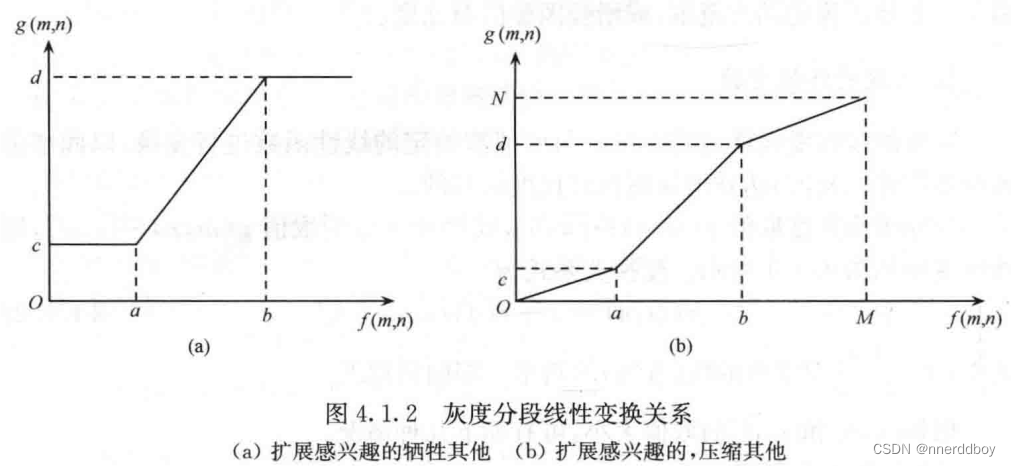
使用场景：

• 对于一张图像，如果某些部分太暗而另一些部分又太亮，灰度分段线性变换可以分别调整这些部分，达到一个较好的整体视觉效果。
• 在需要特别强调或隐藏图像一部分细节时，这种变换可以局部地增强或减弱对比度。

对比

• 简单与复杂：灰度线性变换比较简单，适用于全局性的图像调整；而灰度分段线性变换更复杂，适用于更细致和定制化的调整。
• 灵活性：线性变换对所有像素使用相同的规则，不够灵活；分段线性变换可以对图像的不同部分使用不同的规则，更具灵活性。
• 应用范围：灰度线性变换适用于整个图像需要改善的情况，例如整体亮度调整；灰度分段线性变换适用于图像的局部区域需要不同程度的调整，例如同时调整阴影和高光。

2)完整代码

import cv2
import numpy as np
import matplotlib.pyplot as plt# 读取图像
image = cv2.imread('cell.jpg', cv2.IMREAD_GRAYSCALE)
if image is None:raise ValueError("Could not open or find the image. Check the path.")# 灰度线性变换
def linear_transform(image, alpha=1.5, beta=0):# 新图像 = alpha * 原图像 + betanew_image = cv2.convertScaleAbs(image, alpha=alpha, beta=beta)return new_image# 灰度分段线性变换
def piecewise_linear_transform(image):# 这里定义了一个简单的分段线性函数，实际函数可能需要根据需求调整new_image = np.zeros_like(image)for i in range(image.shape[0]):for j in range(image.shape[1]):if image[i, j] < 128:new_image[i, j] = image[i, j] * 0.5else:new_image[i, j] = image[i, j] * 1.5# 确保值在0-255之间new_image[new_image > 255] = 255return new_image# 应用变换
linear_image = linear_transform(image)
piecewise_image = piecewise_linear_transform(image)# 显示图像
plt.figure(figsize=(15, 5))# 显示原始图像
plt.subplot(1, 3, 1)
plt.imshow(image, cmap='gray')
plt.title('Original Image')
plt.axis('off')# 显示线性变换后的图像
plt.subplot(1, 3, 2)
plt.imshow(linear_image, cmap='gray')
plt.title('Linear Transformation')
plt.axis('off')# 显示分段线性变换后的图像
plt.subplot(1, 3, 3)
plt.imshow(piecewise_image, cmap='gray')
plt.title('Piecewise Linear Transformation')
plt.axis('off')plt.tight_layout()
plt.show()

3)运行结果

(2)灰度对数变换与灰度指数变换

1)原理介绍

灰度对数变换

原理： 灰度对数变换的基本思想是对图像的低亮度值进行更强的变换而对高亮度值进行较弱的变换。这种变换能够将图像中的暗区域中的细节拉伸，而压缩亮区域的对比度。这有助于在图像的暗部分透露更多细节。

使用场景：

• 当图像中有很多阴暗区域，并且这些区域中的细节被隐藏时，灰度对数变换可以使这些细节变得更明显。
• 在图像的动态范围较大时（即图像中同时包含很亮和很暗的区域），这种变换有助于降低动态范围，让整个图像的细节都能够较好地显示出来。

灰度指数变换

原理： 灰度指数变换与对数变换相反，它对图像高亮度区域的影响比暗区域要大。这意味着它可以增加图像亮区域的对比度，使得图像的亮部分更加明亮。

使用场景：

• 当图像的高亮区域细节不是很重要，而希望突出显示暗部细节时，可以使用灰度指数变换。
• 在某些情况下，如果需要模拟图像的视觉效果，使之看起来更亮或者更有光泽感，灰度指数变换也很有用。

对比

• 灰度对数变换通常用于增强图像中的暗部细节，它能够将暗区域的对比度提高，让这些区域的内容更易于观察。
• 灰度指数变换则相反，它更多地增强了亮部的对比度，通常会使图像的亮部更加亮丽。

2)完整代码

import numpy as np
import matplotlib.pyplot as plt
from PIL import Image# 读取图像并转换为灰度
image_path = 'cell.jpg'
original_image = Image.open(image_path).convert('L')
image_array = np.array(original_image)# 灰度对数变换
log_transformed = np.log1p(image_array)  # np.log1p对数组中的每个元素进行log(1+x)运算
log_transformed = (log_transformed / log_transformed.max()) * 255  # 归一化并扩展到0-255范围
log_image = Image.fromarray(np.uint8(log_transformed))  # 将数组转换回图像格式# 灰度指数变换
# 为了避免数值过大，通常会将图像数据先归一化，指数变换后再还原
image_array_normalized = image_array / 255
exp_transformed = np.exp(image_array_normalized)  # np.exp对数组中的每个元素进行e^x运算
exp_transformed = (exp_transformed / exp_transformed.max()) * 255  # 归一化并扩展到0-255范围
exp_image = Image.fromarray(np.uint8(exp_transformed))# 创建一个画布显示原图和变换后的图像
fig, axes = plt.subplots(1, 3, figsize=(15, 5))# 显示原图
axes[0].imshow(original_image, cmap='gray')
axes[0].set_title('Original Image')
axes[0].axis('off')# 显示对数变换图像
axes[1].imshow(log_image, cmap='gray')
axes[1].set_title('Log Transformation')
axes[1].axis('off')# 显示指数变换图像
axes[2].imshow(exp_image, cmap='gray')
axes[2].set_title('Exponential Transformation')
axes[2].axis('off')# 展示图像
plt.tight_layout()
plt.show()

3)运行结果