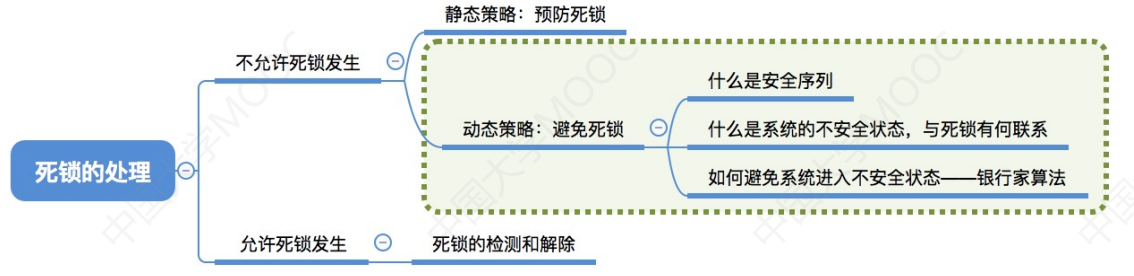
文章目录
- 2.4_3 死锁的处理策略——避免死锁
- (一)什么是安全序列
- (二)安全序列、不安全状态、死锁的联系
- (三)银行家算法
- 总结
2.4_3 死锁的处理策略——避免死锁
银行家算法是“避免死锁”策略的最著名的一个算法。
(一)什么是安全序列
你是一位成功的银行家,手里掌握着100个亿的资金。
有三个企业想找你贷款,分别是企业B、企业A、企业T,为描述方便,简称BAT。
B表示:“我最多会跟你借70亿。”
A表示:“我最多会跟你借40亿。”
T表示:“我最多会跟你借50亿。”
但是,有个规矩:如果你借给企业的钱总数达不到企业提出的最大要求,那么不管你之前给企业借了多少钱,那些钱都拿不回来了。
刚开始,BAT三个企业分别从你这借了20、10、30亿。
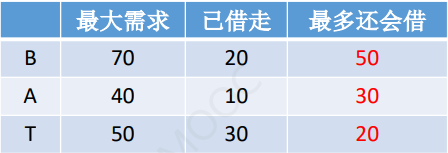
显然,你手上还有40亿。
情况1
手里还有40亿。
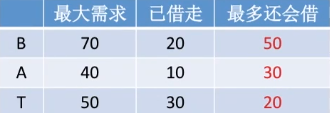
此时,B还想借30亿,你敢借吗?假如我们借给他了,那么情况如下表。
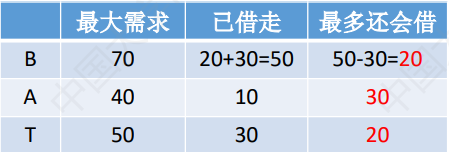
由于刚刚手上还有40亿,且借给了B企业30亿,那么手上还有10亿。
而由上表所示,如果BAT任何一个公司再借20亿,那么自己手上的10亿就满足不了他们的请求。又因为“如果你借给企业的钱总数达不到企业提出的最大要求,那么不管你之前给企业借了多少钱,那些钱都拿不回来了”的这个规矩,所以你最终借出去的所有钱都收不回来了。
因此,在刚刚B向你再借30亿的时候,你就不应该借给他。即,给B借30亿是不安全的。
情况2
手里还有40亿。
此时,A还想借20亿,你敢借吗?假如我们借给他了,那么情况如下表。
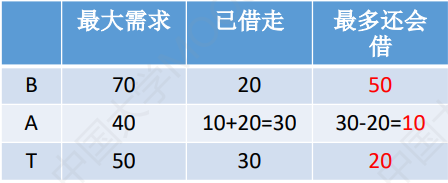
由于刚刚手上还有40亿,且借给了A企业20亿,那么手上还有20亿。
接下来,情况就比较乐观了,这个局就不是一个死局了。
1.你可以先把20亿全部借给T,等T把钱全部还回来,手里就会有50亿,再把这些钱全部借给B,B还钱后就会有70亿,最后再借给A。
2.或者,先借给A企业10亿,等A还钱,手里就有了50亿,再借给T企业20亿,等T还钱,手里就有了80亿,最后再借给B。
即:“A还想再借20亿”是安全的,并且再借给A后,按照T ---> B ---> A的顺序借钱是可以的,而按照A ---> T ---> B的顺序借钱也是可以的。
(二)安全序列、不安全状态、死锁的联系
经过分析,我们发现:有的资源请求是不能答应的,而有的资源请求是可以答应的。
不安全:

给B借30亿是不安全的。借出之后手里只剩10亿,如果接下来BAT任何一个企业再借20亿,那么任何一个企业都得不到满足。就成为一个死局。
安全:

给A借20亿是安全的,因为存在T ---> B ---> A这样的安全序列。
所谓安全序列,就是指如果系统按照这种序列分配资源,则每个进程都能顺利完成。只要能找出一个安全序列,系统就是安全状态。当然,安全序列可能有多个。
如果分配了资源以后,系统中找不出任何一个安全序列,系统就进入了不安全状态。这就意味着之后可能所有进程都无法顺利的执行下去。当然,如果有进程提前归还了一些资源,那系统也有可能重新回到安全状态,不过我们在分配资源之前总是要考虑到最坏的情况。
如果系统处于安全状态(即,至少存在一个安全序列),就一定不会发生死锁。如果系统进入不安全状态(即,找不到任何一个安全序列),就可能发生死锁(处于不安全状态未必就是发生了死锁,但发生死锁时一定是在不安全状态)。
因此可以在资源分配之前预先判断这次分配是否会导致系统进入不安全状态,以此决定是否答应资源分配请求。这也是“银行家算法”的核心思想。
(三)银行家算法
银行家算法是荷兰学者Dijkstra为银行系统设计的,以确保银行在发放现金贷款时,不会发生不能满足所有客户需要的情况。后来该算法被用在操作系统中,用于避免死锁。
接下来思考一下,怎么把这种用于银行系统的算法,运用到操作系统的避免死锁上面?
核心思想:在进程提出资源申请时,先预判此次分配是否会导致系统进入不安全状态。如果会进入不安全状态,就暂时不答应这种请求,让该进程先阻塞等待。
思考:BAT的例子中,只有一种类型的资源——钱。但是在计算机系统中会有多种多样的资源(打印机、扫描仪、摄像头……),应该怎么把算法拓展为多种资源的情况呢?
其实很简单,我们只需要把一维的数字(仅代表钱)拓展为多维的向量。
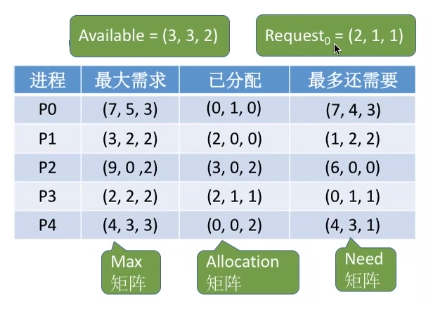
比如:系统中有5个进程P0-P4,3种资源R0-R2,初始数量为(10, 5, 7)。则某一时刻的情况可表示如下。
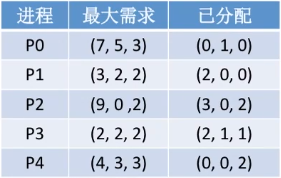
根据上表,此时已分配了(7, 2, 5),还剩余(3, 3, 2)。
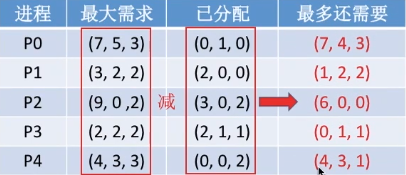
再根据“每个进程最多还需要”的数量,判断此时是否处于安全状态。
问题:此时系统是否处于安全状态?
方案:可以尝试着看看能不能找到一个安全序列。
依次检查剩余可用资源(3, 3, 2)是否能满足各进程的需求。
可满足P1需求,将P1加入安全队列,并更新剩余可用资源值为(5, 3, 2)。
经过从前到后的检查,首先发现P1进程可以满足。那么,我们优先把剩余资源分配给P1的话,P1是一定可以顺利结束的,而一旦P1顺利结束了,P1就会归还资源。于是,资源数就会增加到
(2, 0, 0) + (3, 3, 2) = (5, 3, 2)。
依次检查剩余可用资源(5, 3, 2)是否能满足剩余进程(不包括已加入安全序列的进程,如下图所示)的需求。
可满足P3需求,将P3加入安全序列,并更新剩余可用资源值为(7, 4, 3)。
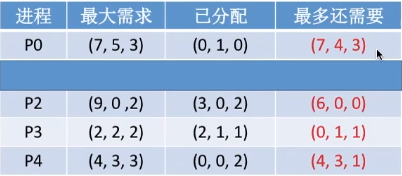
经过从前到后的检查(P1已加入安全序列,不检查P1),首先发现P3进程可以满足。那么,如果优先把资源分配给P3,P3一定是可以顺利执行结束的。等P3结束了就会归还资源。于是,资源数就会增加到
(2, 1, 1) + (5, 3, 2) = (7, 4, 3)。
依次检查剩余可用资源(7, 4, 3)是否能满足剩余进程(不包括已加入安全序列的进程)的需求……
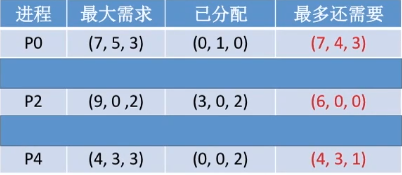
以此类推,共五次循环检查即可将5个进程都加入安全序列中,最终可得一个安全序列:{P1, P3, P0, P2, P4}。
该算法称为安全性算法。可以很方便地用代码实现以上流程,每一轮检查都从编号较小的进程开始检查。
实际做题时可以更快速的得到安全序列。因为实际做题的时候是用笔算的,没必要按照代码逻辑执行的那么严谨。说明如下,
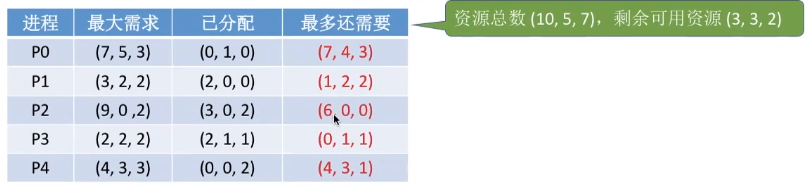
还是刚才的题。资源总数
(10, 5, 7),此时系统剩余可用资源(3, 3, 2)。
如果从手算的视角来观察,经过对比,(3, 3, 2)可以给P1,也可以给P3。因此,可以一并将P1、P3都加入安全序列。同时,计算P1、P3归还资源之后的剩余资源值。更新剩余资源值为(2, 0, 0) + (2, 1, 1) + (3, 3, 2) = (7, 4, 3)。
因为,
(3, 3, 2)如果能满足P1,那么待分配给P1,等P1使用完归还资源,这样之后,手上的剩余资源只会比(3, 3, 2)更多。因此一定能继续满足P3的使用。所以,当我们对于这种情况进行考虑时,就不需要考虑的这么麻烦。我们只需要考虑,把资源给P1、P3之后的情况,而不需要再机械的遵循代码运行逻辑。
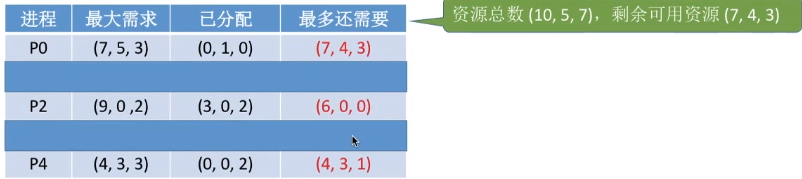
同理,此时剩余资源(7, 4, 3),可以给P0、可以给P2、也可以给P4。因此,可以一并将P0、P2、P4都加入安全序列。同时,更新剩余资源值。
于是,5个进程全部加入安全序列,说明此时系统处于安全状态,暂时不可能发生死锁了。
再举一个“找不到安全序列”的例子。
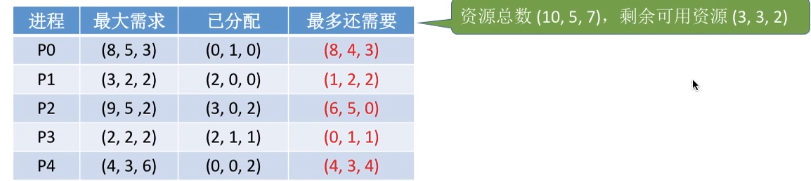
首先,经过对比,(3, 3, 2)可满足P1、P3,因此可以把P1、P3加入安全序列。并更新此时剩余资源值为(2, 0, 0) + (2, 1, 1) + (3, 3, 2) = (7, 4, 3)。
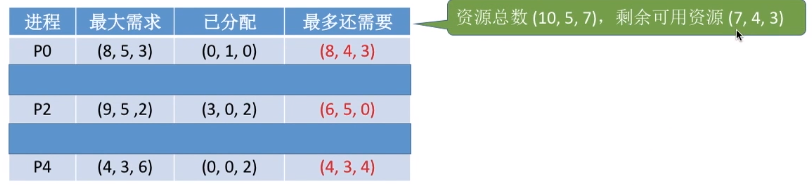
继续对比,对于剩下的进程,P0、P2、P4都得不到完全满足(向量中的各个分量,只要有一个得不到满足,就无法满足)。
于是,无法找到任何一个安全序列。说明此时系统处于不安全状态,有可能发生死锁。
如何用代码实现银行家算法
假设系统中有n个进程,m种资源。
每个进程在运行前先声明对各种资源的最大需求数,则可用一个n * m的矩阵(可以用二维数组实现)表示所有进程对各种资源的最大需求数。不妨称之为最大需求矩阵Max。在矩阵中,每个元素Max[i, j] = k表示进程Pi最多需要k个资源Rj。
系统还需要记录“此时已经给每个进程分配了多少资源”。同理,可以使用一个n * m的分配矩阵Allocation表示对所有进程的资源分配情况。
至于每个进程“最多还需要多少资源”,我们只需使用Max - Allocation即可,并同样使用一个二维矩阵保存之。不妨称之为Need矩阵,表示各进程最多还需要多少各类资源。
此外,还需要记录“系统中剩余资源的数量”。对此,我们使用一个一维数组即可。可以使用一个长度为m的一维数组Available表示当前系统中还有多少可用资源。
当某进程Pi向系统申请资源时,可用一个长度为m的一维数组Requesti表示本次申请的各种资源的数量。
各个数据结构都已设置好,接下来考虑如何进行操作。
可用银行家算法预判本次分配是否会导致系统进入不安全状态:
1.如果Requesti[j] <= Need[i, j](0 ≤ j ≤ m),便转向2,否则认为出错(因为它本次申请的资源数量超过了它“最多还需要”的资源数量)。
2.如果Requesti[j] <= Available[j](0 ≤ j ≤ m),便转向3,否则表示尚无足够资源,Pi必须等待。
3.系统试探着把资源分配给进程Pi,并修改相应的数据(并非真的分配,修改数值只是为了做预判,看看是否安全,最终确认安全了才会开始分配资源)。
Available = Available - Requesti;
Allocation[i, j] = Allocation[i, j] + Requesti[j];
Need[i, j] = Need[i, j] - Requesti[j]。
4.操作系统执行安全性算法,检查此次资源分配后,系统是否处于安全状态。若安全,才正式分配;否则,恢复相应数据,让进程阻塞等待。
所谓的“安全性算法”,就是逐个对比,看看当前剩余资源能否满足其中某个进程的最大需求。若有一个可满足的,则将该进程加入安全序列,并使得此进程归还所有它持有的资源。如果所有进程都不能满足,则此时是不安全状态。
总结
数据结构的设置
1.长度为m的一维数组Available表示还有多少可用资源;
2.n * m矩阵Max表示各进程对资源的最大需求数;
3.n * m矩阵Allocation表示已经给各进程分配了多少资源;
4.Max - Allocation = Need矩阵表示各进程最多还需要多少资源;
5.用长度为m的一维数组Requesti表示进程此次申请的各种资源数。
银行家算法步骤
1.检查此次申请是否超过了之前声明的最大需求数;
2.检查此时系统剩余的可用资源是否还能满足这次请求;
3.试探着分配,更改各数据结构;
4.用安全性算法检查此次分配是否会导致系统进入不安全状态。
安全性算法步骤
检查当前的剩余可用资源是否能满足某个进程的最大需求,如果可以,就把该进程加入安全序列,并把该进程持有的资源全部回收。
不断重复上述过程,看最终是否能让所有进程都加入安全序列。
注意:系统处于不安全状态未必死锁,但死锁时一定处于不安全状态。系统处于安全状态一定不会死锁。


)
)

C题思路)
)


)



——基于GPU部署踩坑)

)



》之概述篇 - 我为什么要翻译介绍美国人工智能科技公司IAB 系列(2))