问题一: namenode -format重复初始化
出现问题的原因是重复初始化时会重新生成集群ID,而dn还是原先的集群ID,两者不匹配时无法启动相应的dn进程。
怎么查找问题原因:在logs目录下找到对应节点的.log文件,使用tail -200 文件名来查看日志信息。
解决办法1:修改data/name/路径下的version文件中的集群ID为老的集群ID,事实修改后仍然报错,初始化不只是集群ID不一致,建议使用方法2:。
解决办法2:删除hadoop文件中的data文件和logs文件。
问题二:免密登录配置出错,permission denied没有权限;拒绝访问
重新使用加密算法生成公钥私钥,并将公钥发送给相应的主机。
ssh-keygen -t rsassh-copy-id hadoop10xxx
常用的端口号
| rpc内部通信 | http外部web端口 | |
|---|---|---|
| namenode | 8020 | 50070 / 9870 |
| mapreduce | 8088 | 8088 |
| 历史服务器 | 19888 | 19888 |
集群的时间同步
- 有网络的情况
- systemctl start ntpd:开启网络时间同步
- systemctl status ntpd : 查看开启状态
- 没有外部网络的情况
sudo vim /etc/ntp.conf:设置102作为基准服务器ntpdate hadoop102: 向102发送请求同步时间sudo crontab -e: 设置定时任务
HDFS文件系统
概述
全称为Hadoop distributed file system, 是一个分布式文件系统,通过目录树来定位文件。适合一次写入,多次读出的场景。一个文件经过创建、写入和关闭之后就不能改变。
- 优点:
- 高容错性:通过增加副本的形式,提高容错性;副本丢失后会自动补全
- 适合处理大数据:数据规模达到PB级别,文件数量达到9亿个
- 可以构建在廉价机器上
- 缺点:
- 不适合低延时数据访问,比如毫秒级的存储数据。
- 无法高效对大量小文件进行存储,小文件存储的寻址时间超过了读取时间
- 不支持并发写入,文件随机修改。仅支持数据的追加,不支持随机修改。
组成架构
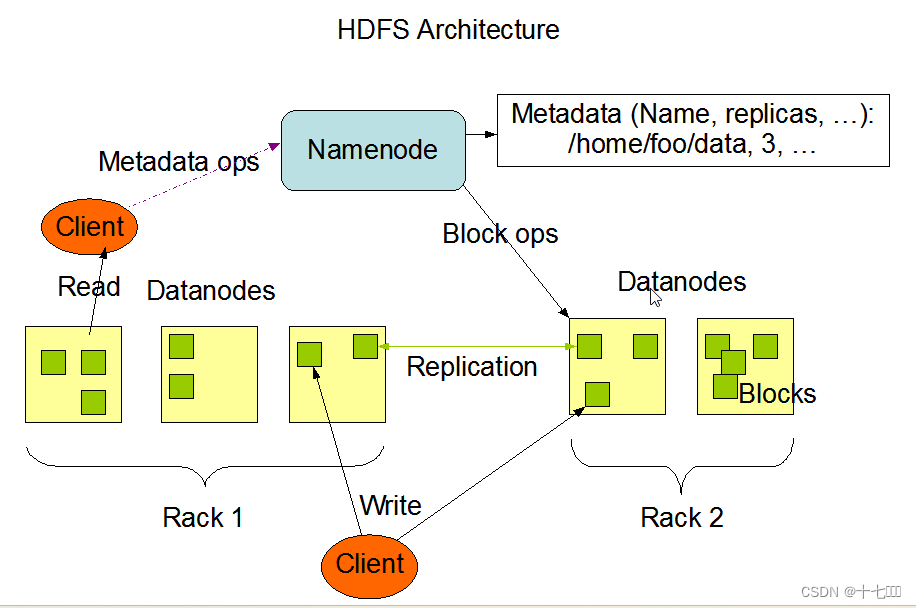
- NameNode:主管
- 管理HDFS的名称空间
- 配置副本策略
- 管理数据块映射信息
- 处理客户端读写请求
- DataNode: 工人
- Client:客户端
- 文件切分,上传之前就切分。
- 如果上传后切分,有可能存不下
- 上传后切分,有三个备份,需要多切几次。
- 管理HDFS,如namenode格式化
- 文件切分,上传之前就切分。
- SecondaryNameNode:辅助NameNode,并非热备。
文件块大小
由磁盘的传输速率决定,由于目前磁盘的传输速率为100M/s,按照程序员的进制进行整数转换为2进制则为128。
根据专家的结论:寻址时间为传输时间的1%时,是最佳状态。
- 文件块太小会增加寻址时间
- 文件块太大,磁盘传输数据的时间会明显大于定位这个块开始位置所需的时间。大于1%这个最佳状态。
hdfs文件操作系统的常用命令
- hadoop fs 等价于 hdfs dfs
- 上传文件到hdfs文件系统
hadoop fs -copyFromLocal caocao.txt /sanguo: 上传hadoop fs -moveFromLocal liubei.txt /sanguo:上传后删除hadoop fs -put sunquan.txt /sanguo:上传hadop fs appendToFIle sunquan.txt /sanguo/liubei.txt:追加文件内容
- 从hdfs文件系统下载文件到本地
hadoop fs -copyToLocal /sanguo/liubei.txt ./:拷贝下载hadoop fs -get /README.txt ./: 拷贝下载hadoop fs moveToLocal: 剪切到本地,暂时没有实现
hadoop fs -ls /sanguo: 查询文件列表hadoop fs -cat /sanguo/caocao.txt: 查看文件内容hadoop fs -chmod 77 /sanguo/caocao.txt: 修改文件权限hadoop fs -du /sanguo: 查询文件夹下的文件的大小hadoop fs -setrep 10 /sanguo/caocao.txt:设置副本数量
HDFS的API操作
IDEA常用快捷键
- 双击shift : 搜索框
- ctrl + h: 查询当前类的父子关系
- ctrl + F12: 查询当前类的所有方法
- ctrl+p: 显示方法的形参列表
- ctrl+alt+f:快速将局部变量提升为全局变量
配置文件优先级
- 代码中的conf.set
- resources目录下的xxx-site.xml配置文件
- jar包中的xxx-default.xml配置文件






——点云投影到圆柱)

)


十二:通用详情组件封装实现)






)
