以下内容有任何不理解可以翻看我之前的博客哦:吴恩达deeplearning.ai专栏
文章目录
- 倾斜数据集的误差指标
- 罕见病预测
- 精确率和召回率
- 精确率和召回率的权衡
- 精确率和召回率的矛盾关系
- F1算法
倾斜数据集的误差指标
在神经网络中,如果你的数据集中正例和负例的比例差距很大,远远不及50比50,那么你的神经网络很可能效果不佳,让我们举个例子。
罕见病预测
假设你的神经网络需要预测一种罕见病,它在正常人群中的发病率约为0.5%,且你的数据集中只有0.5%代表你的预测为负,那么用以前的算法,你就很难估计你算法的性能,例如你有一个算法仅仅会打印1,结果它的准确度为99.5%,另一个算法预测的准确度为98%,这并不能说明下面这个算法的准确性不如上面一个算法。,因此我们需要一个方法,能够减少预测为1的权重,从而增加预测错误的代价。即不同的错误度量。

精确率和召回率
首先,你需要创建一个2*2的混淆矩阵,其中,第一行第一列的格子代表真实为1,且预测也为1的数量;第一行第二列的格子代表真实为0,预测为1的数量;第二行,第一列代表真实为1,预测为0的格子;第二行第二列代表真实与预测都为0的格子。
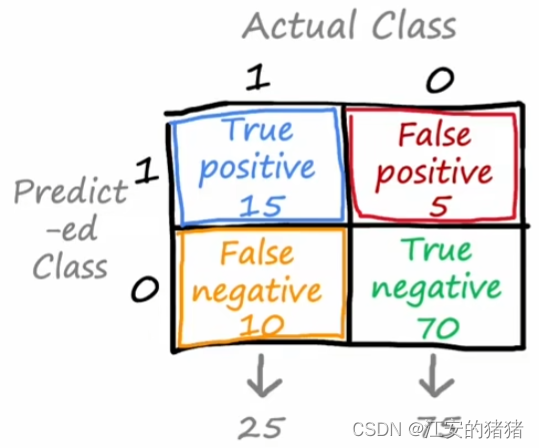
精确率定义为:
t r u e p o s t r u e p o s + f a l s e p o s \frac{true\:pos}{true\:pos+false\:pos} truepos+falsepostruepos
这代表在你预测为真的事件中,有多少预测正确。
召回率定义为:
t r u e p o s t r u e p o s + f a l s e n e g \frac{true\:pos}{true\:pos+false\:neg} truepos+falsenegtruepos
这代表在所有真事件中,你预测正确的占多少。
当你的算法在精确度和召回率都能有比较高的表现时,那么说明你的算法是一个好算法。
精确率和召回率的权衡
在理想情况下,我们总是希望算法既能拥有高精确率也能拥有高召回率。高精确率意味着你预测为患病的患者中真的患病的可能性大,高召回率说明你识别错误真的患病的患者的概率小。但事实上,我们经常需要在这两者间进行取舍,我们看看该如何做。
精确率和召回率的矛盾关系
我们在逻辑回归中,逻辑回归输出的值位于 0 < f ( x ) < 1 0<f(x)<1 0<f(x)<1之间,当 f ( x ) f(x) f(x)预测值大于等于0.5是,我们判断为1,小于0.5时,判断为0。
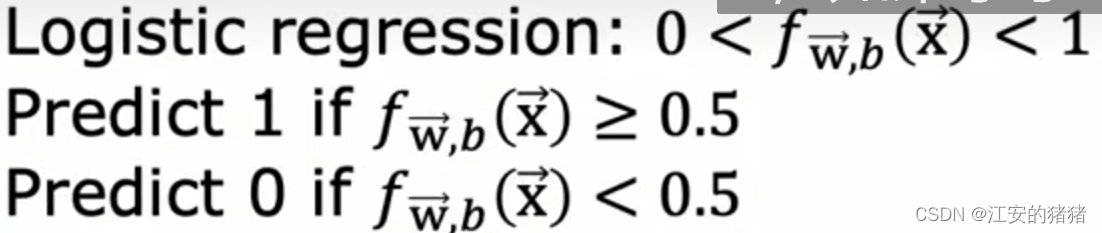
假设有一种疾病,它的治疗代价很昂贵,但是如果不治疗,也不会产生很严重的后果,那么此时,你可以将预测的临界值从0.5改为0.9,甚至是1。既仅当你非常确定时,才会判断这个人患病。那么此时,算法就具有高精确率,低召回率。
相反,如果这个疾病治疗起来很容易,但是一旦没有被发现,那么后果会很严重,那么抱着宁错杀一千,不放过一个的想法,你可以将临界值从0.5往下调,既低精确率,高召回率。

当然,你有些时候也希望能全都要,事实上,精确率和召回率满足如下曲线:
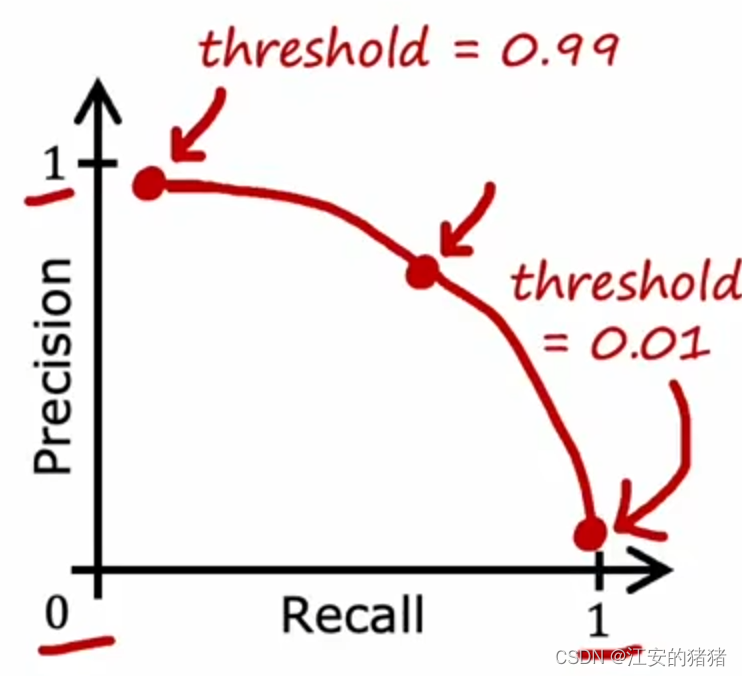
所以在这种需求之下,例如图中的红点,选择一个Precision下降还没有很多的点,同时也能保持高Recall。
当你手动选择阈值的时候就需要这样做。
事实上,有时候你也可以让机器来替你选择一个适中的回归率和精确率,这就要提到一种F1算法,让我们举例来说明。
F1算法
假设你构建了三种算法,它们分别具有:适中的精确率和召回率;高精确率低召回率;低精确率和高召回率,那么你该如何判断三个算法哪个更好呢?一种最先想到的方法是取平均值,但是这其实并不合理,因为这是一种偏向于大值的算法,如果一个算法具有低精确率和高召回率,那么很有可能是数据样本中的该数据过少导致,结果平均值算法还把该算法认为性能很好,这就不合适了。
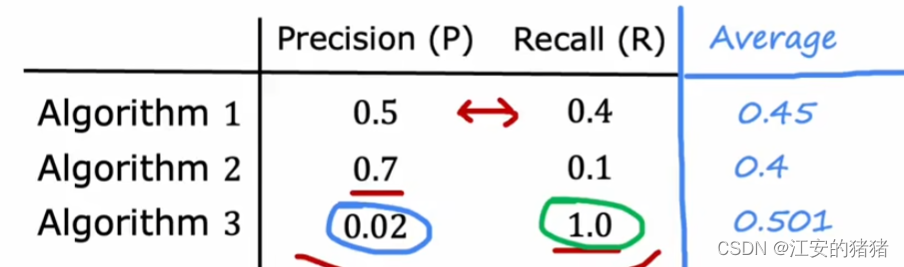
而F1算法的公式如下:
F 1 s c o r e = 1 1 2 ( 1 P + 1 R ) F1\;score=\frac{1}{\frac{1}{2}(\frac{1}{P}+\frac{1}{R})} F1score=21(P1+R1)1
这是一种更加强调小值的算法。我们知道,过低的精确率和召回率说明这个算法并不十分有效,而这个算法可以发现这一点:
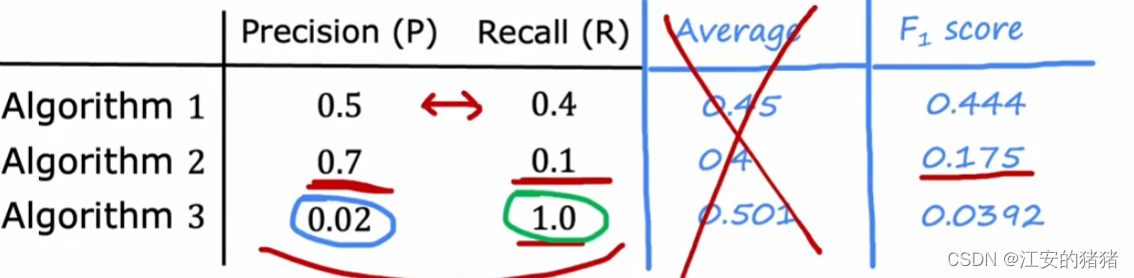
在F1公式下,我们可以得到算法一的分数最高,比较合适了
为了给读者你造成不必要的麻烦,博主的所有视频都没开仅粉丝可见,如果想要阅读我的其他博客,可以点个小小的关注哦。

 。void f(int *p){ *p = 5;}int main(void){ int a, *p; a = 10;)



除F2题外补题报告)


规划模型)



)






