CSP-202109-2-非零段划分

关键点：差分数组

详见：【CSP考点回顾】差分数组

时间复杂度分析

使用差分数组的优势在于，它将问题转化为了在一次遍历中识别并利用关键变化点（波峰和波谷），从而避免了对每个可能子数组的重复检查。这种方法利用了问题的特殊结构——即只有在特定的转折点才需要更新我们的计数——来大幅度减少必要的计算量。因此，在处理大数据量时，差分数组方法的效率远高于暴力枚举法。

1. 暴力枚举法（70分）：

   • 在暴力枚举方法中，尝试每个可能的子数组，然后检查每个子数组是否符合条件（是否是非零段）。对于每个长度为 n 的数组，有 $n(n+1)/2$ 种可能的子数组（因为我们可以从数组的每个位置开始，选择不同的结束位置）。
   • 对于每个子数组，我们需要 $O(m)$ 的时间来验证它是否是一个非零段，其中 m 是子数组的长度。因此，总的时间复杂度将会是 $O(n^3)$（因为对于每个子数组我们都进行了线性时间的检查）。

2. 差分数组法（100分）：

   • 使用差分数组的方法，我们首先通过一次遍历（ $O(n)$ 时间复杂度）处理原数组来建立差分数组，并进行初始化处理（例如，标记波峰和波谷）。
   • 接下来，我们再次遍历差分数组（又是 $O(n)$ 时间复杂度）来计算最长的非零段。在这次遍历中，我们累积差分值，并记录最大的累积值。
   • 因此，整个过程的时间复杂度是 $O(n)+O(n)=O(n)$，远低于暴力枚举方法的 $O(n^3)$。

解题思路

1. 使用向量 A，在其开始和结束位置添加额外的零元素，以符合问题中提到的非零段定义。
2. 使用 unique 函数对数组 A 进行去重，即连续重复的元素只保留一个，因为连续的相同值不会影响非零段的长度。
3. 通过遍历数组 A，计算差分数组 diff，在波峰位置加一，在波谷位置减一。这里波峰指的是 A[i] 比它前后的元素都要大的情况，波谷指的是 A[i] 比它前后的元素都要小的情况（详见下图）。

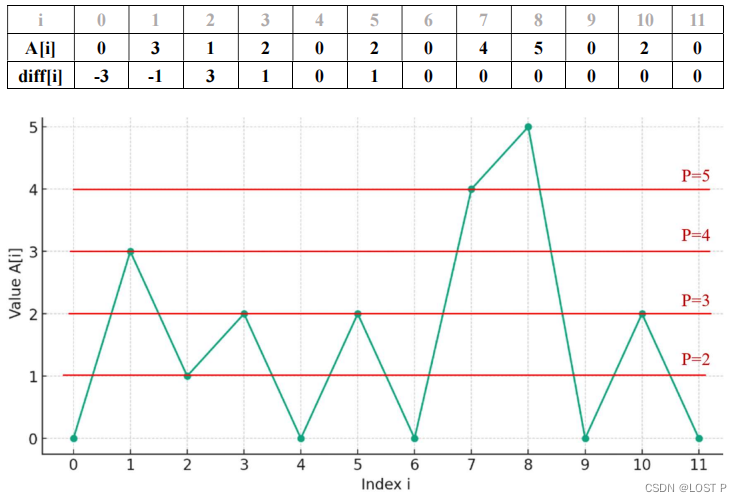
在这个问题中，使用“波峰”和“波谷”的概念来加一或减一，实际上是利用差分数组的特性来标记数组中的重要转变点。我们利用差分数组来记录特定模式的出现——即数组中的极值点。

1. 为什么在波峰位置加一：
   • 波峰定义为一个元素，其值大于其前后的元素（A[i-1] < A[i] > A[i+1]）。在这个位置加一是为了标记一个上升段的结束和下降段的开始。这是非零段可能的开始或结束，因为在实际应用中，一个上升然后下降的序列（波峰）意味着我们找到了一个完整的子段，这可能是我们寻找的非零段的一部分。
2. 为什么在波谷位置减一：
   • 波谷定义为一个元素，其值小于其前后的元素（A[i-1] > A[i] < A[i+1]）。在这个位置减一是为了标记一个下降段的结束和上升段的开始。这也是非零段可能的开始或结束，因为它标志着一个低谷，即从高值下降到低值的转变点。

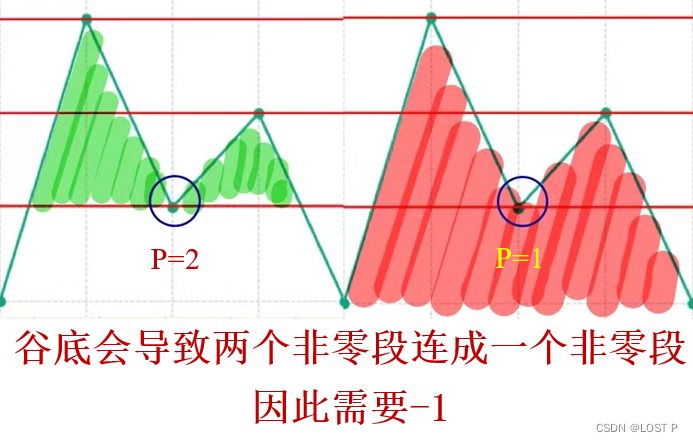
4. 遍历差分数组 diff，累加当前值到 sum，并更新 noneZeroMax，用来记录遇到的最大的非零段长度。sum 的计算方式保证了我们只在非零段内进行计数，并且每次遇到非零段时都检查是否能更新最大长度。

完整代码

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;int n, sum, noneZeroMax;
vector<int>diff(50000); // 差分数组int main() {cin >> n;vector<int>A(n + 2, 0); // A的第一个和最后一个元素置零（非零段定义）for (int i = 1; i <= n; i++){cin >> A[i];}auto last = unique(A.begin(), A.end()); // 去重A.erase(last, A.end());// 计算差分数组：波峰+1，波谷-1for (int i = 1; i <= A.size() - 2; i++){if (A[i - 1] < A[i] && A[i] > A[i + 1]) diff[A[i]]++;if (A[i - 1] > A[i] && A[i] < A[i + 1]) diff[A[i]]--;}// 统计最大非零段for (int i = diff.size()-1; i >= 0; i--){sum += diff[i];noneZeroMax = max(sum, noneZeroMax);}cout << noneZeroMax;return 0;
}