链表完了之后就是我们的栈和队列了,当然我们的STL中也有实现,下面我们先来看一下简单用法,跟我们之前C语言实现的一样,stack和queue有这么几个重要的成员函数

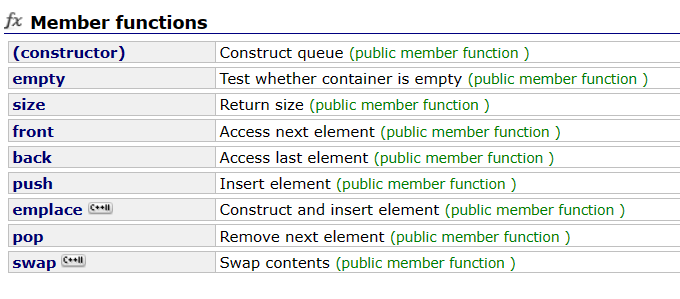
最主要的就是这么几个:empty,push,pop,top(front),size,为什么要说这几个重要的呢?因为我们发现,stack和queue并没有我们之前的容器的迭代器,说明它们跟之前学的容器并不同,它们叫做适配器。
什么叫做适配器呢?我们听过笔记本电脑的电源适配器,它就是将220V的电压转化成电脑需要的电压,所以适配器的本质是转换。回到我们这里,stack和queue这个适配器就可以将其他的容器转换成实例化后的stack和queue


我们可以看到,类模板的第二个参数是要传一个容器,当然不传也行,它是有缺省值的,这里的缺省值是deque,这个容器是介于vector和list之间的,为什么要有一个这样的容器呢?
我们首先来总结一下vector和list的优缺点
vector:优点是下标随机访问和缓存命中率高(缓存命中率就是指比如我要给定vector中连续几个元素的值,我要一个一个给定,当我给定第一个的时候,它并不是只把第一个给定到内存中,而是把它及周围的位置都拿到了内存中,这样我给定第二个值时,就不需要再拿入到内存中了),缺点是前面部分插入删除效率低,扩容有消耗
list:优点是任意位置插入删除效率高和按需申请释放(每次就申请一个节点的空间,不会浪费),缺点是不支持下标随机访问,缓存命中率低
我们可以来试一下
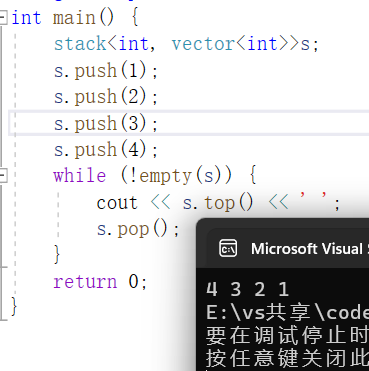
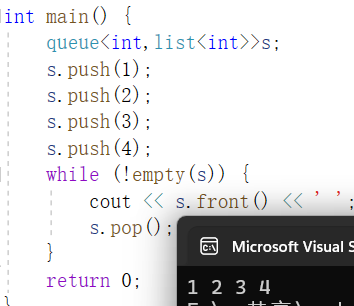
既然如此,我们要模拟实现的话,就不用像之前那么写了,而是跟库一样,模板参数传个容器,下面的几个关键函数赋用容器的就可以了
template<class T,class container>
class stack {
public:void push(const T& x) {_con.push_back(x);}void pop() {_con.pop_back();}bool empty() {return _con.size() == 0;}const T& top() {return _con.back();}size_t size() {return _con.size();}
private:container _con;
};template<class T, class container>
class queue {
public:void push(const T& x) {_con.push_back(x);}void pop() {_con.pop_front();}bool empty() {return _con.size() == 0;}const T& front() {return _con.front();}size_t size() {return _con.size();}
private:container _con;
};下面来几道有关的题来帮助我们更好的使用
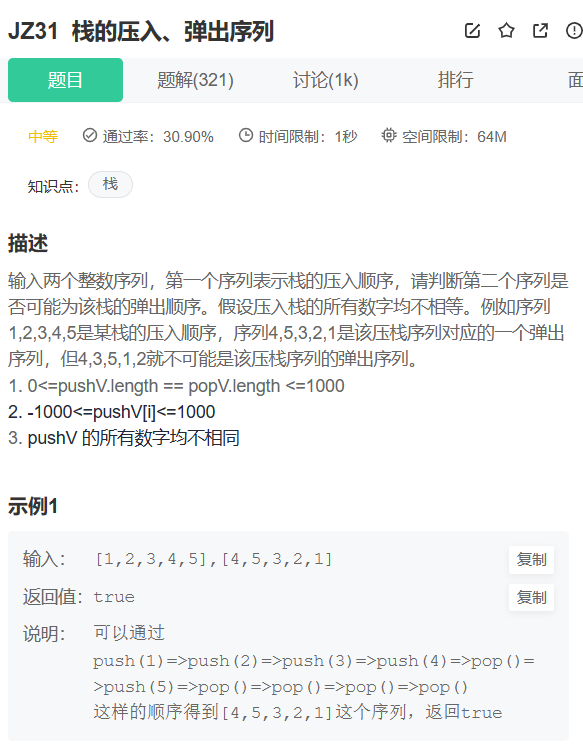
这个题其实就是模拟我们人脑在做这种题时的想法,我们一般先看弹出顺序的第一个,然后看怎么怎么压入才会让它第一个弹出。第一个其实跟后边几个都一样,最后走到头,看栈是否为空,为空就是符合
class Solution {public:bool IsPopOrder(vector<int>& pushV, vector<int>& popV) {stack<int>s;int n = popV.size();for (int pushi = 0, popi = 0; pushi < n && popi < n;) {while (s.empty() || s.top() != popV[popi]) {s.push(pushV[pushi++]);if (pushi == n)break;}while (!s.empty() && s.top() == popV[popi]) {s.pop();popi++;}}if (s.empty())return true;return false;}
};
这里实际上就是给你一个后缀表达式,让你求出表达式的值,我们人一般看的就是中缀表达式,那么后缀表达式是什么呢?其实就是把运算符放到两个操作数的后面。所以解题思路就是看到数字就入栈,看到运算符就从栈中取两个值进行运算,把结果再放到栈中,直到把后缀表达式走完
class Solution {
public:int evalRPN(vector<string>& t) {
stack<int>st;
for(auto e:t){if(e=="+"||e=="-"||e=="*"||e=="/"){int right=st.top();st.pop();int left=st.top();st.pop();
switch(e[0]){case '+':st.push(left+right);break;case '-':st.push(left-right);break;case '*':st.push(left*right);break;case '/':st.push(left/right);break;
}}else st.push(stoi(e));
}
return st.top();}
};我们这里是给定一个后缀表达式,那么我们应该如何求一个中缀表达式的后缀表达式呢?我这里简单实现了一下,可以传一个string,string里面要么是字母用来表示数字,要么是+-*/
string postfix(string s) {stack<char>st;string ret;for (int i = 0; i < s.size();) {char e = s[i];if (e == '+' || e == '-' || e == '*' || e == '/') {if (st.empty()) {st.push(e);i++;}else if ((e == '*' || e == '/') && (st.top() == '+' || st.top() == '-')) {st.push(e);i++;}else {ret += st.top();st.pop();}}else if (e == '(') {int j = i;int k = j;int num = 1;for (k = j+1; k < s.size(); k++) {if (s[k] == '(')num++;if (s[k] == ')'&&num==1)break;if (s[k] == ')')num--;}string tmp(s.begin() + j + 1, s.begin() + k);ret += postfix(tmp);i+=k-j+1;}else {ret += e;i++;}}while (!st.empty()) {ret += st.top();st.pop();}return ret;
}先简单说一下一个正常的式子转后缀表达式是什么逻辑,先说没有括号的情况下
给一个string,从左向右开始:先创建一个栈
1.如果遇到非运算符,直接写入到最终结果中
2.如果遇到运算符,(1).如果栈为空或此运算符比栈顶运算符的优先级高,那么就入栈;(2).如果优先级相等或低,那么栈顶元素出栈,放到最终结果,继续仍然用此运算符进行下一轮判断
一直循环,直到string结束,最后把栈中的都移入到最终结果
如果有括号,将括起来的部分进行函数递归,重复上述过程,把递归完之后的结果加入到最终结果中

层序遍历肯定是要用到队列的,这个题的返回值告诉我们要一层一层的给到vector中,这就要求我们记录下每一层的节点个数才可以
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {vector<vector<int>> ret;if (root == nullptr)return ret;queue<TreeNode*> qu;qu.push(root);int levelsize = qu.size();while(!qu.empty()){vector<int>f;while(levelsize--){TreeNode* tmp=qu.front();qu.pop();f.push_back(tmp->val);if(tmp->left!=nullptr)qu.push(tmp->left);if(tmp->right!=nullptr)qu.push(tmp->right);}ret.push_back(f);levelsize=qu.size();}return ret;}
};)













-新手笔记(主外键,视图))


——Socket套接字)

