有意向获取代码，请转文末观看代码获取方式~
展示出图效果
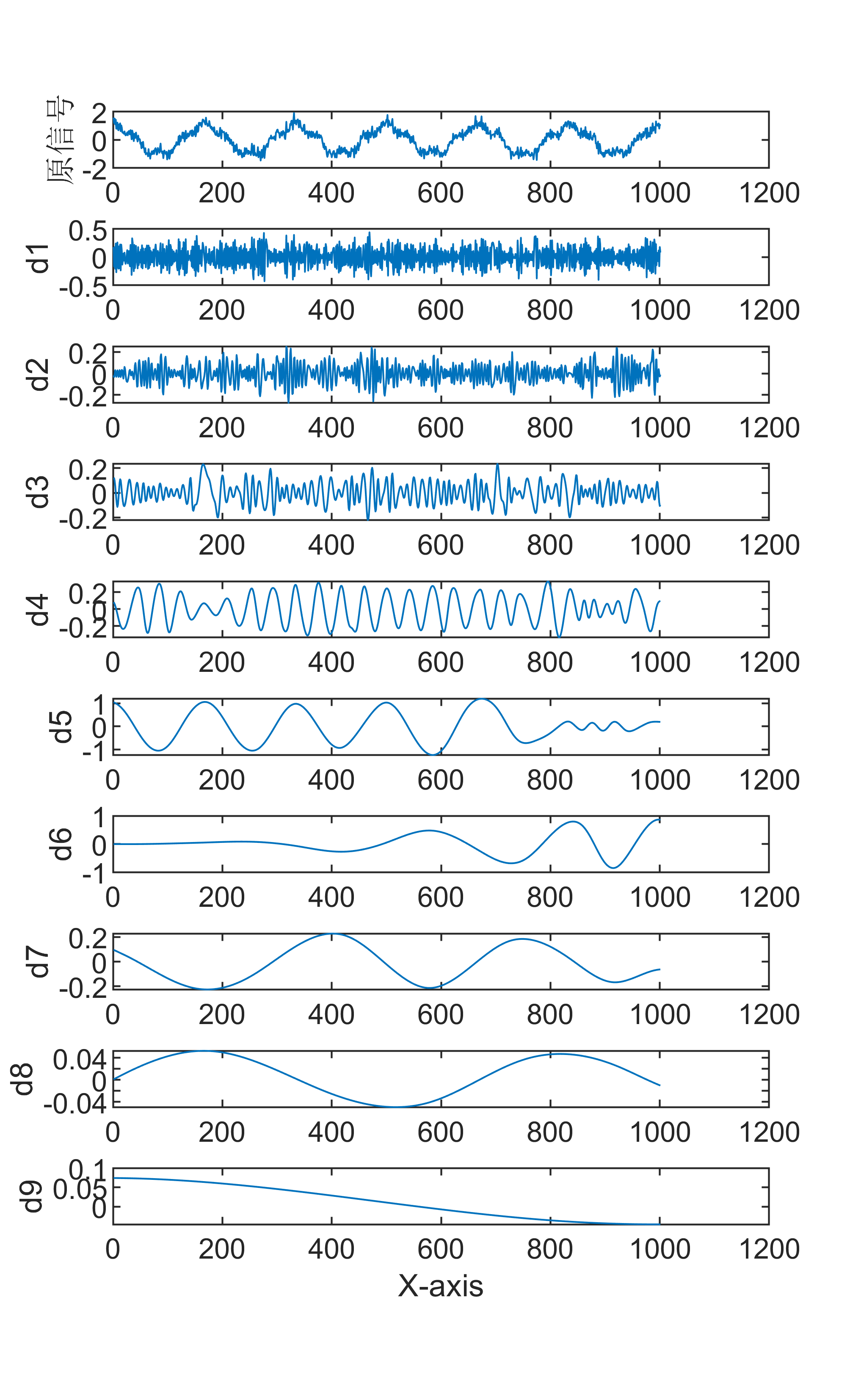
1 EMD信号分解算法
EMD 分解又叫经验模态分解，英文全称为 Empirical Mode Decomposition。
EMD 是一种信号分解方法，它将一个信号分解成有限个本质模态函数 (EMD) 的和，每个 EMD 都是具有局部特征的振动模式。EMD 分解的主要步骤如下：
-
将信号的局部极大值和极小值连接起来，形成一些局部极值包络线。
-
对于每个局部极值包络线，通过线性插值得到一条平滑的包络线。然后将原信号减去该包络线，得到一条局部振荡的残差信号。
-
对于该残差信号，重复步骤1和2，直到无法再分解出新的局部振荡模式为止。
-
将所有的局部振荡模式相加，得到原始信号的EMD分解。 EMD分解的优点是能够很好地处理非线性和非平稳信号，并且不需要预先设定基函数。因此，EMD分解在信号处理、图像处理和模式识别等领域得到了广泛的应用。
要想在 MATLAB 中使用 EMD 分解首先要安装 EMD 分解的 MATLAB 工具包。
关于简短的代码视频教程均可关注B站、小红书、知乎同名账号（Lwcah）观看教程~
EMD 工具包的安装：在 MATLAB 打开 package_emd 文件夹，运行 install_emd. M 以及 index_emd. M 两个函数如下图所示即可完成工具包的安装。
MATLAB 信号分解第一期-EMD请转:
MATLAB | 信号分解全家桶详情请参见：
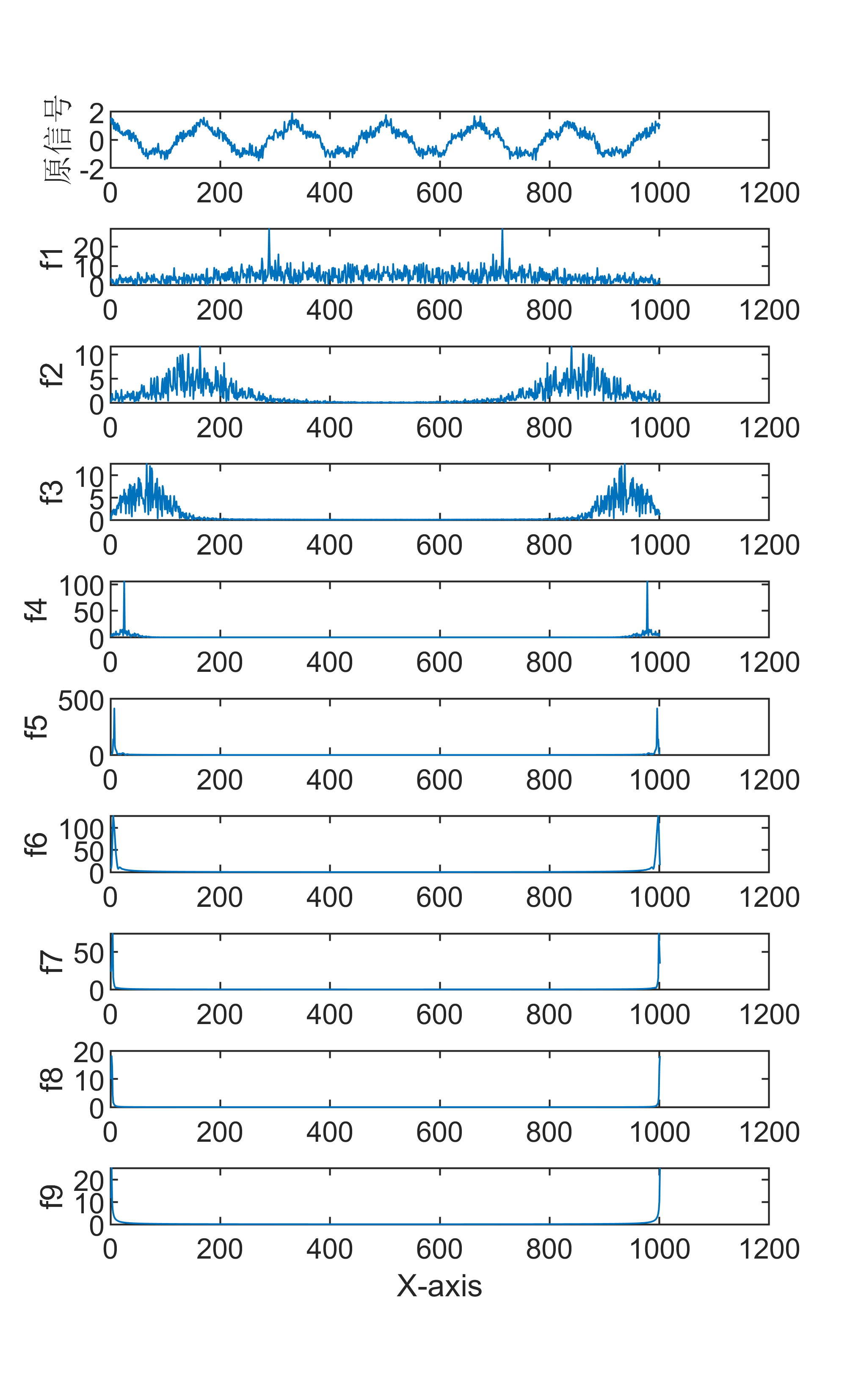
2 FFT傅里叶频谱变换算法
傅里叶变换是一种数学方法，用于将一个信号分解成一系列正弦和余弦函数的和，从而更好地理解和处理信号。傅里叶变换在信号处理领域有着广泛的应用，包括音频处理、图像处理等。 具体来说，傅里叶变换的步骤如下：
-
给定一个连续时间域函数f(t)，其中t为时间。
-
对f(t)进行傅里叶变换，得到它的频率域表示F(ω)，其中ω为角频率。
-
F(ω)表示了f(t)中所有频率分量的幅度和相位信息。
-
将F(ω)分解成一系列正弦和余弦函数的和，即： F(ω) = ∑[a(k)cos(kω) + b(k)sin(kω)] 其中，k为频率分量的序号，a(k)和b(k)分别为对应的正弦和余弦函数的系数。 傅里叶变换的优点是可以将时间域中的信号转换成频率域中的信号，从而更好地理解信号的频率分量和周期性特征，同时也方便进行一些信号处理任务，例如滤波、降噪等。缺点是傅里叶变换需要对整个信号进行处理，计算量较大，在实时处理等场景下可能会存在较大的延迟。
MATLAB | 频谱分析算法 | 傅里叶变换 开源 MATLAB 代码请转:
MATLAB | 9种频谱分析算法全家桶详情请参见：
3 EMD信号分解+FFT傅里叶频谱变换组合算法
如下为简短的视频操作教程。
【MATLAB 】 EMD信号分解+FFT傅里叶频谱变换组合算法请转:
【MATLAB 】信号分解+FFT傅里叶频谱变换组合算法全家桶详情请参见：
关于代码有任何疑问，可以一起探讨科研，写作，代码等诸多学术问题，我们一起进步~
代码见附件~
)
)