1. 汉诺塔问题

原题链接
题干:
算法原理:
利用递归算法
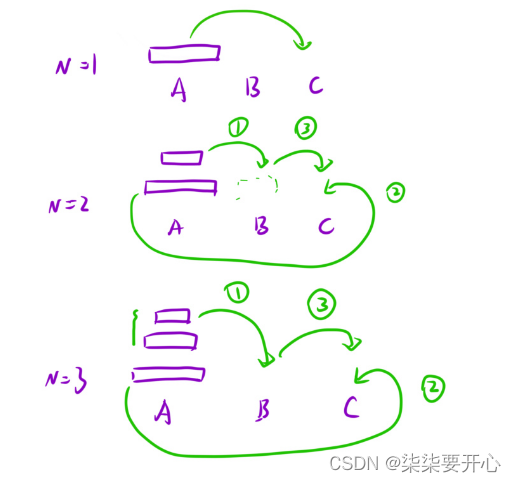
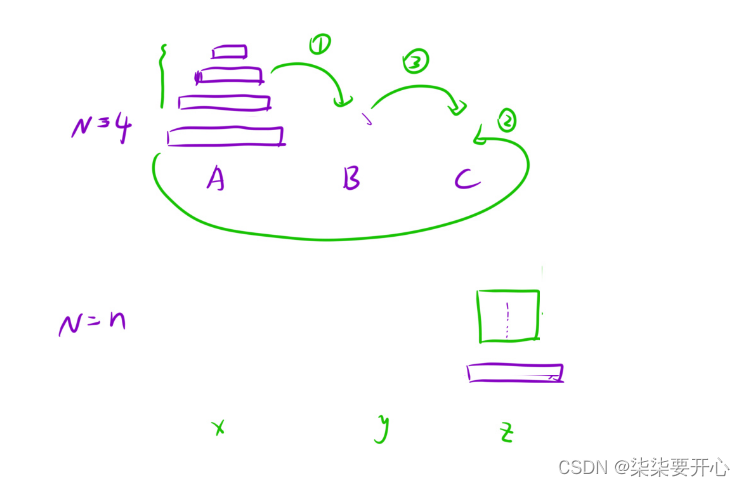
将x柱子上的一堆盘子,借助 y柱子,转移到z 柱子上面
递归函数流程:
- 当前问题规模为 n=1 时,直接将 A 中的最上面盘子挪到 C 中并返回
- 递归将 A 中最上面的 n-1 个盘子挪到 B 中
- 将 A 中最上面的⼀个盘子挪到 C 中
- 将 B 中上面 n-1 个盘子挪到 C 中
代码:
class Solution {public void hanota(List<Integer> a, List<Integer> b, List<Integer> c) {dfs(a, b, c, a.size());}public void dfs(List<Integer> a, List<Integer> b, List<Integer> c, int n) {if(n == 1) {c.add(a.remove(a.size() - 1));return;}dfs(a, c, b, n - 1);c.add(a.remove(a.size() - 1));dfs(b, a, c, n - 1);}
}
2. 合并两个有序链表
原题链接
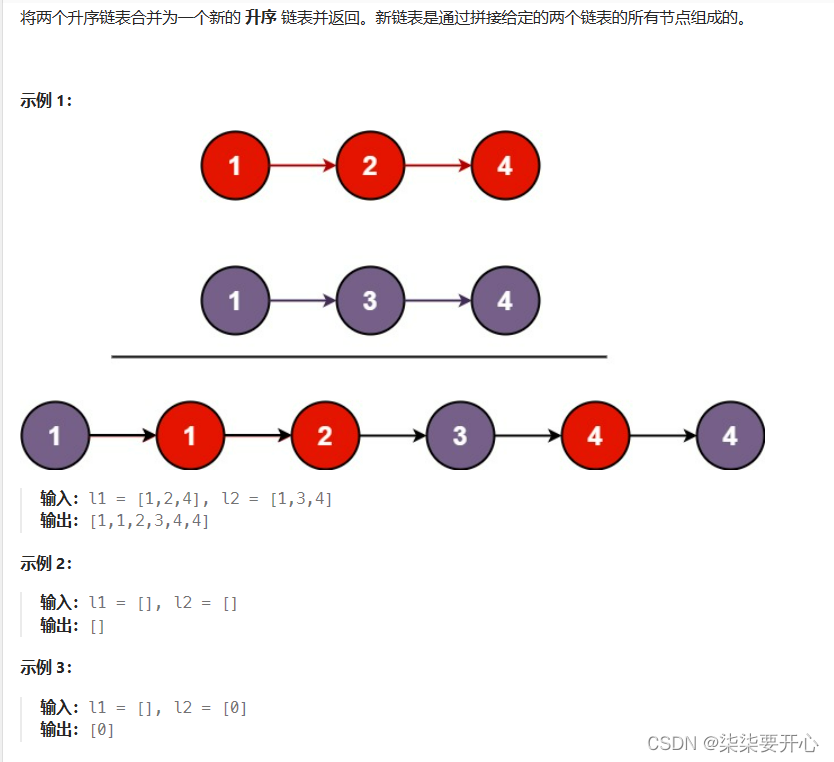
题干:
升序 链表
新链表是通过拼接给定的两个链表的所有节点组成的
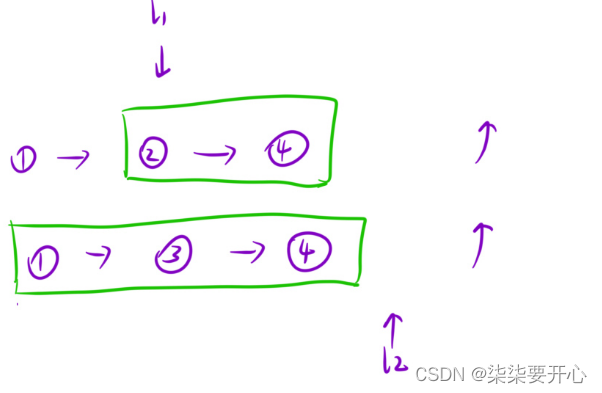
算法原理:
-
重复子问题(函数头的设计)
合并两个有序链表 -
只关心一个子问题咋做什么(函数体的设计)
选择两个头结点中较小的结点作为最终合并后的头结点,然后将剩下的链表交给递归函数去处理 -
递归的出口
谁为空返回另一个
代码:
class Solution {public ListNode mergeTwoLists(ListNode l1, ListNode l2) {if(l1 == null) {return l2;}if(l2 == null) {return l1;}if(l1.val <= l2.val) {l1.next = mergeTwoLists(l1.next, l2);return l1;}else {l2.next = mergeTwoLists(l1, l2.next);return l2;}}
}
3. 反转链表
原题链接
题干:
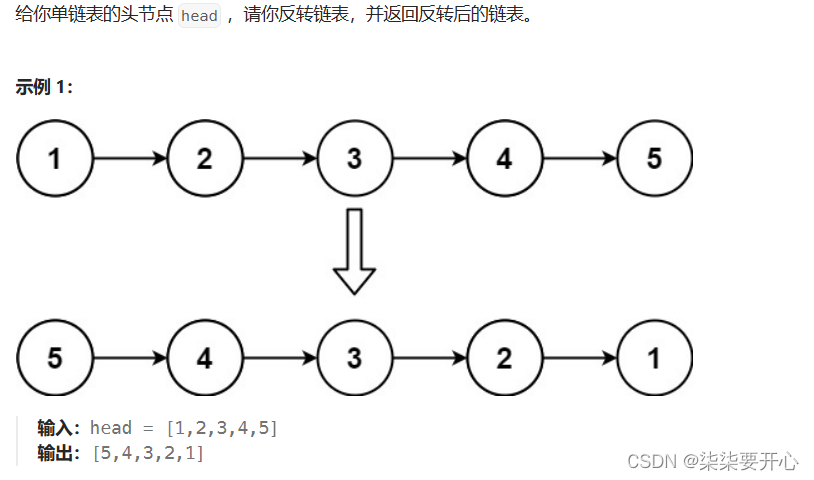
单链表的头节点 head ,反转链表,并返回反转后的链表
算法原理:
利用递归
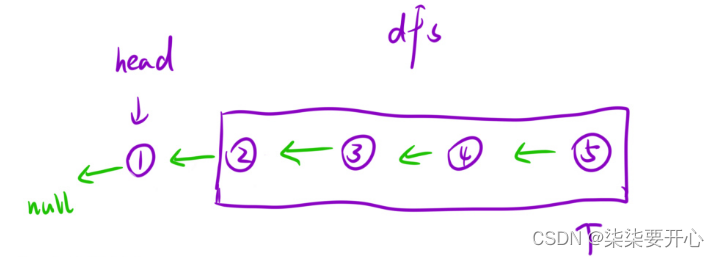
- 从宏观角度
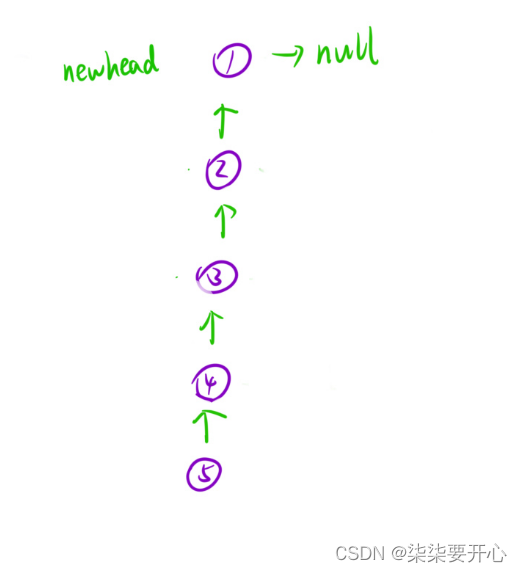
1)让当前节点后面的链表先逆序,并且把头结点返回
2)让当前节点添加到逆置后的链表的后面 - 将链表看成一棵树
仅需做一次 dfs 即可
后序遍历
代码:
class Solution {public ListNode reverseList(ListNode head) {if(head == null || head.next == null) {return head;}ListNode newheader = reverseList(head.next);head.next.next = head;head.next = null;return newheader;}
}
4. 最大子数组和

原题链接
题干:
一个整数数组 nums
找出一个具有最大和的连续子数组
算法原理:
1. 状态表示:
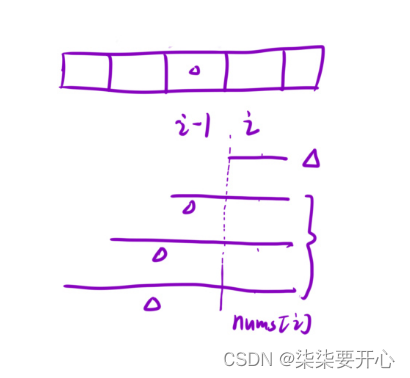
dp[i] 表示:以 i 位置为结尾的所有子数组中的最大和
2. 状态转移方程
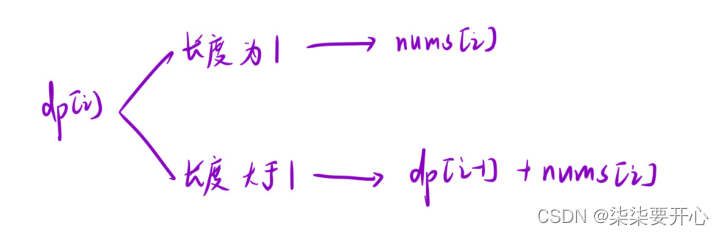
dp[i] = max(nums[i], dp[i - 1] + nums[i])
3. 初始化
- 辅助结点里面的值要「保证后续填表是正确的」
- 「下标的映射关系」
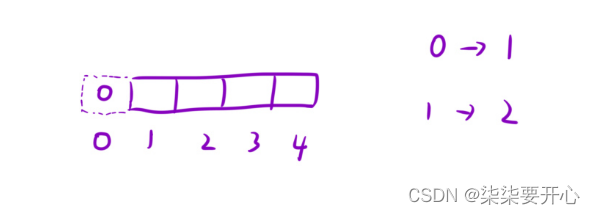
4. 填表顺序
从左往右
5. 返回值
整个dp表的最大值
代码:
class Solution {public int maxSubArray(int[] nums) {int n = nums.length;int[] dp = new int[n + 1];int ret = Integer.MIN_VALUE;for(int i = 1; i <= n; i++) {dp[i] = Math.max(nums[i - 1], dp[i - 1] + nums[i - 1]);ret = Math.max(ret, dp[i]);} return ret;}
}
5. 环形子数组的最大和

原题链接
题干:
长度为 n 的环形整数数组 nums
返回 nums 的非空 子数组 的最大可能和
算法原理:
1. 状态表示:

2. 状态转移方程

f[i] = max(nums[i], f[i - 1] + nums[i])

g[i] = min(nums[i], g[i - 1] + nums[i])
3. 初始化
- 辅助结点里面的值要「保证后续填表是正确的」
- 「下标的映射关系」
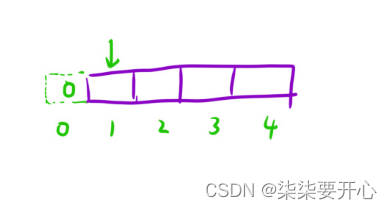
4. 填表顺序
从左往右
5. 返回值
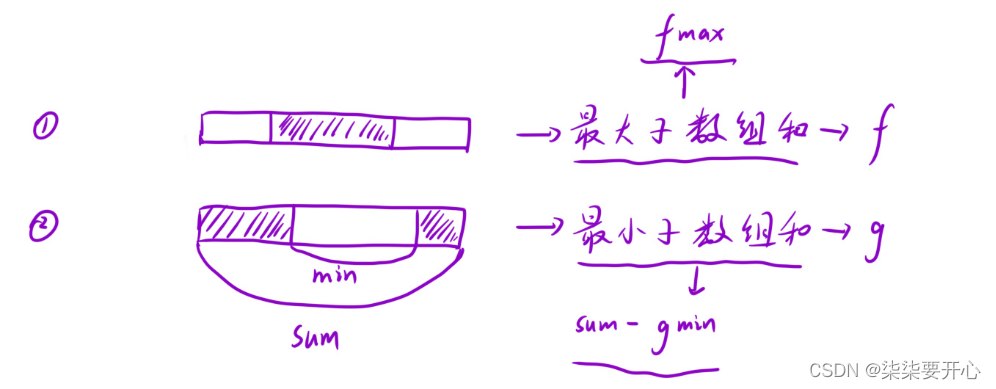
- 先找到 f 表里面的最大值 -> fmax
- 找到 g 表里面的最小值 -> gmin
- 统计所有元素的和 -> sum
- 返回 sum == gmin ? fmax : max(fmax, sum - gmin)
代码:
class Solution {public int maxSubarraySumCircular(int[] nums) {int n = nums.length;int[] f = new int[n + 1];int[] g = new int[n + 1];int sum = 0;int fmax = Integer.MIN_VALUE;int gmin = Integer.MAX_VALUE;for(int i = 1; i <= n; i++) {int x = nums[i - 1];f[i] = Math.max(x, x + f[i - 1]);fmax = Math.max(fmax, f[i]);g[i] = Math.min(x, x + g[i - 1]);gmin = Math.min(gmin, g[i]);sum += x;}return sum == gmin ? fmax : Math.max(fmax, sum - gmin);}
}




)






)

)


)


