前言

滑动窗口作为一个考点较高的算法，广泛应用于子串问题中，本文将进行详细讲解。

一、滑动窗口是什么

滑动窗口是双指针算法的一种，基本思路为维护一个窗口，然后从前往后遍历元素进行运算。

二、滑动窗口算法和其他双指针算法的区别

双指针算法常见的为三种：

1. 快慢指针算法（常用于链表有环判断）
2. 双向指针（两个指针一个从最左，一个从最右出发进行查找），典型应用为二分查找
3. 滑动窗口（两个指针一前一后出发，两个指针中间维持一个窗口结构

快慢指针代码如下（示例）：

public static boolean hasCycle(ListNode head) {ListNode slow = head;if(slow == null) return false;ListNode fast = head.next;while(fast != null && fast.next != null){if(slow == fast) return true;slow = slow.next;fast = fast.next.next;}return false;}

双向指针指针代码如下（示例）：

int l = 0, r = len;
while(l < r){int mid = l + r >> 1;if(num[mid] > 0){r = mid - 1;}else if(num[mid] == 0){return mid;}else{l = mid + 1;}
}

滑动窗口代码示例如下：

   // 固定窗口大小为 kstring s;// 在 s 中寻找窗口大小为 k 时的所包含最大元音字母个数int  right = 0;while(right < s.size()) {window.add(s[right]);right++;// 如果符合要求，说明窗口构造完成，if (right>=k) {// 这是已经是一个窗口了，根据条件做一些事情// ... 可以计算窗口最大值等 // 最后不要忘记把 right -k 位置元素从窗口里面移除}}return res;   

三、滑动窗口原理讲解

滑动：说明窗口不是固定不变的，而是具有一定的可变性的

窗口：窗口并不是一定固定不变的，可以进行扩大，然后逐步进行缩小直到满足情况

为了便于理解，这里采用的是字符串来讲解。但是对于数组其实也是一样的。滑动窗口算法的思路是这样：

我们在字符串 S 中使用双指针中的左右指针技巧，初始化 left = right = 0，把索引闭区间 [left, right] 称为一个「窗口」。

我们先不断地增加 right 指针扩大窗口 [left, right]，直到窗口中的字符串符合要求（包含了 T 中的所有字符）。

此时，我们停止增加 right，转而不断增加 left 指针缩小窗口 [left, right]，直到窗口中的字符串不再符合要求（不包含 T 中的所有字符了）。同时，每次增加 left，我们都要更新一轮结果。

重复第 2 和第 3 步，直到 right 到达字符串 S 的尽头。

这个思路其实也不难，第 2 步相当于在寻找一个「可行解」，然后第 3 步在优化这个「可行解」，最终找到最优解。左右指针轮流前进，窗口大小增增减减，窗口不断向右滑动。

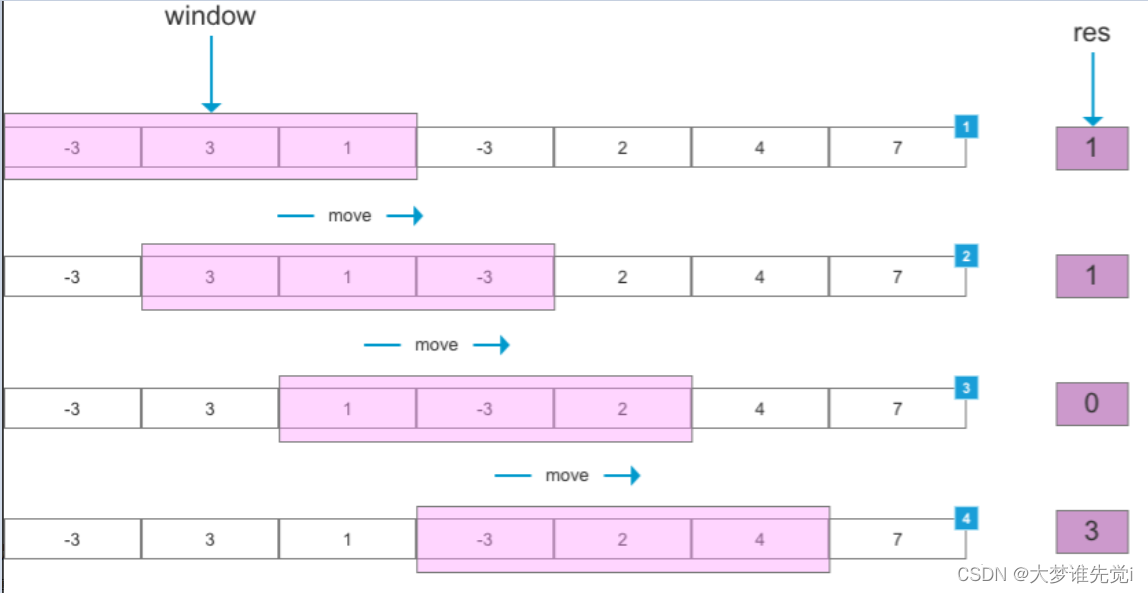
流程图如下：

算法模版如下：

int left = 0, right = 0;while (right < s.size()) {// 增大窗口window.add(s[right]);right++;while (window needs shrink) {// 缩小窗口window.remove(s[left]);left++;}
}

四、例题讲解

例题1： 无重复字符的最长子串
给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

示例 1:
输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”，所以其长度为 3。

示例 2:
输入: s = “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”，所以其长度为 1。

示例 3:
输入: s = “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”，所以其长度为 3。
请注意，你的答案必须是 子串 的长度，“pwke” 是一个子序列，不是子串。

代码如下：

class Solution {public int lengthOfLongestSubstring(String s) {int len = s.length();int[] arr = new int[150];int temp = 0;int ans = 0;for(int i = 0, j = 0; i < len; i++){temp = s.charAt(i);arr[temp]++;while(arr[temp] > 1 && j < i){arr[s.charAt(j)]--;j++;}ans = ans > i - j + 1 ? ans : i - j + 1;}return ans;}
}

例题2：找到字符串中所有字母异位词
给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

异位词 指由相同字母重排列形成的字符串（包括相同的字符串）。

示例 1:
输入: s = “cbaebabacd”, p = “abc”
输出: [0,6]
解释:
起始索引等于 0 的子串是 “cba”, 它是 “abc” 的异位词。
起始索引等于 6 的子串是 “bac”, 它是 “abc” 的异位词。

示例 2:
输入: s = “abab”, p = “ab”
输出: [0,1,2]
解释:
起始索引等于 0 的子串是 “ab”, 它是 “ab” 的异位词。
起始索引等于 1 的子串是 “ba”, 它是 “ab” 的异位词。
起始索引等于 2 的子串是 “ab”, 它是 “ab” 的异位词。

代码如下：

class Solution {public List<Integer> findAnagrams(String s, String p) {int len = p.length();int len1 = s.length();int[] times = new int[26];int[] now = new int[26];ArrayList<Integer> res = new ArrayList<>();for(int i = 0; i < len; i++){times[p.charAt(i) - 'a']++; }for(int l = 0, r = 0; r < len1; r++){now[s.charAt(r) - 'a']++;if(r - l + 1 < len){continue;}while(r - l + 1 > len){now[s.charAt(l++) - 'a']--;}if(Arrays.equals(now,times)){res.add(l);}}return res;        }
}