【数据结构】哈希

在一个数据序列中查找某一个数据元素，是数据管理时经常涉及的，通常以比较的方式来完成，典型的案例有无序序列的暴力查找（O(N)）、有序序列的二分查找（O(logN)）、平衡搜索树（O(logN)）等。但它们所处理的数据元素，与其所在序列中的存储位置并没有明确的关系，数据元素在序列中的位置是随机的。因此在查找某一个数据时，可能需要进行数次的数据比较，也就是说，它们的查找效率往往取决于查找过程中数据元素的比较次数。而当数据达到一定量级，继续通过比较的方式，显然查找的代价较大且效率较低，情况并不理想。而最理想的情况应当是直接就能找到需要的数据。那么，是否存在一种更高效的方案，可以不通过比较，就直接找到一个数据呢？

20世纪50年代，德国计算机科学家汉斯·彼得·卢恩(Hans Peter Luhn)为计算机解读信息、快速搜索信息提供了一种新的、被称为哈希函数（Hash Function，或称散列函数）的方案。数据元素通过哈希函数可以得到其在序列中的存储位置，使每一个数据元素与其所在序列中的存储位置建立起一个映射关系，模拟出“每一个数据元素在序列中的位置是确定的”；存储位置通过哈希函数可以还原成数据元素的值，模拟出“每一个数据元素都可以被直接访问”（最快能达到O(1)）。而由“数据元素-哈希函数-存储位置”构造的数据结构，就称为哈希表（Hash table，或称散列表）。

本篇博客梳理了哈希思想和相关数据结构，并搭配对STL源码中线性探测、哈希桶、位图、布隆过滤器的模拟实现，旨在更好地帮助读者理解哈希的功能和适用情景。

一、常见的哈希函数

1.直接定址法（最常用）

2.除留余数法（最常用）

3.平方取中法

4.折叠法

5.随机数法

6.数学分析法

二、哈希冲突与解决方法

1.哈希冲突

2.闭散列

2-1.线性探测

2-2.二次探测

3.闭散列的模拟实现

3-1.基本结构

3-2.插入

3-3.查找和删除

3-4.完整代码

4.开散列

5.开散列的模拟实现

5-1.基本结构

5-2.查找

5-3.插入

5-4.删除

5-5.特别的析构

5-6.完整代码

三、哈希的应用

1.哈希表

2.位图

2-1.原理与应用

2-2.模拟实现

3.布隆过滤器

3-1.原理与应用

3-2.模拟实现

补、海量数据问题

1.位图相关

2.布隆过滤器相关

3.哈希切割

一、常见的哈希函数

哈希函数本质是一个数学表达式，作用是将数据元素的值（或称关键码）转换为数据元素在哈希表中的存储位置（或称哈希地址，最常见的形式是数组下标）。

【补】哈希函数设计原则

定义域：必须包含所有要存储的数据元素；
值域：当一个哈希表有m个地址的大小时，哈希函数的值域必须在0到m-1之间；
通过哈希函数得到的地址能均匀分布在哈希表中；
表达式应简洁明了。

1.直接定址法（最常用）

直接定址法的表达式为：

Hash（Key）= A*Key + B

其中，key为数据元素的值， A和B为两个未知数，它们的值视具体情景而定。表达式的结果即为数据元素的存储位置。

直接定址法的表达式十分简洁，结果地址分布较为均匀，但使用前需确定数据元素值的分布情况，适用于数据量小且数据值连续分布（值的分布范围集中）的情景。

最典型的情景多与字符有关，因为字符的分布范围就是连续（集中）的。

例如用一个大小为26的int类型的数组character来存26个英文小写字母，要使character[0]='a'，character[1]='b'...只需将小写字母的ASCII码值（a对应97，b对应98）通过
表达式“1 * ASCII码值 - 97 = 数组下标”（“1 * 97 - 97 = 0”，“1 * 98 - 97 = 1”）求得字符'a'、字符'b'...在数组中的下标并存入数组即可。

又例如这道题目“字符串中第一个不重复的字符”，在一个字符串中找到它第一个不重复的字符，并返回它的下标——

class Solution {
public:int firstUniqChar(string s) {unordered_map<int, int> frequency; //unordered_map相当于是map的不排序但去重版本，同样存的是<key, value>//这里的key代表字母的ASCII码，value代表出现次数for (char ch: s) {++frequency[ch]; //将字符的出现次数统计在unordered_map中}for (int i = 0; i < s.size(); ++i) { //将字符从前往后挨个在unordered_map查询，就能找到第一个不重复的字符if (frequency[s[i]] == 1) { //不重复的字符的出现次数为1return i; }}return -1; //没有找到则返回-1}
};//来源：力扣官方题解

2.除留余数法（最常用）

除留余数法的表达式为：

Hash(key) = key % p (p<=m)

其中，key为数据元素的值，m为哈希表的大小（元素个数），p是一个不大于m（或等于m）的质数。表达式的结果即为数据元素的存储位置。

除留余数法适用于值的分布范围分散的情景。

例如要将一个数据集合{1，7，6，4，5，9}存入一个大小为10的int类型的数组中，已知m=10，取p=10，则通过等式“数值 % 10 =下标”可以求得每个数据在数组中的下标。

3.平方取中法

平方取中法适用于数据元素值的分布不明确，但值本身不是特别大的情景，一般取值平方的中间n位作为数据元素的存储位置。

例如一个数据元素的值为1234，值的平方为1522756，取值平方的中间3位，“227”就是它的地址。又例如一个数据元素的值为4321，值的平方为18671041，取值平方的中间3位，“671(或710)”就是它的地址。

4.折叠法

折叠法适合数据元素值的分布不明确，但值本身特别大（位数较多）的情景。它是将数据元素的值从左到右分割成位数相等的几部分(一般最后一部分位数可以稍短)，然后将这几部分叠加求和，并按哈希表的大小，取后n位作为数据元素的存储位置。

例如一个数据元素的值为123456，取每3位为一组将值分割为123和459，再将它们叠加求和求得579，取最后一位9作为数据元素的存储位置。

5.随机数法

随机数法适用于数据元素值的长度不相等的情景。取一个随机数函数，将数据元素值通过随机数函数求得的结果作为它的存储位置，通式为Hash(key) = random(key)，其中random即为随机数函数。

6.数学分析法

数学分析法适用于数据元素的值特别大（位数较多），且位数本身分布均匀、重复较少的情景。

设有n个d位数，每一位可能有r种不同的符号，这r种不同的符号在各个位上出现的频率不一定相同，每种符号出现的机会均等，在某些位上分布比较均匀，在某些位上分布不均匀但只有某几种符号经常出现。可根据哈希表的大小，选择其中各种符号分布均匀的若干位作为数据元素的存储位置。

例如要存储某家公司员工登记表，将手机号作为数据元素，选择手机号后四位作为存储位置。

二、哈希冲突与解决方法

1.哈希冲突

例如在除留余数法的案例中，要将一个数据集合{1，7，6，4，5，9}存入一个大小为10的int类型的数组中，每一个数据都恰好有自己独立的存储位置。

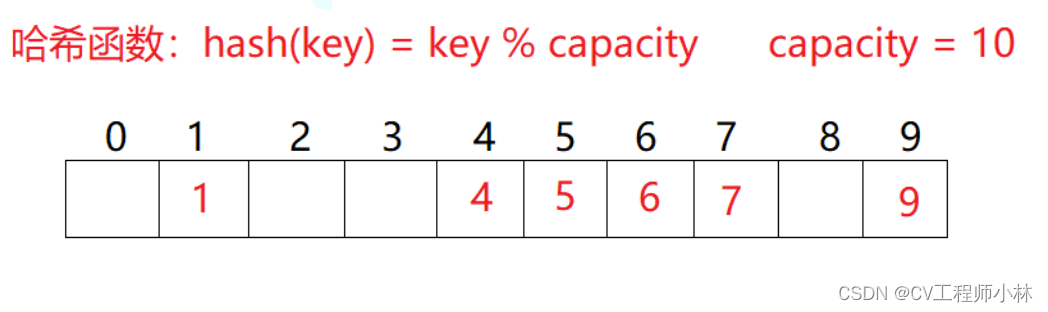
若此时再按除留余数法，向数组中放入数据44，则数据44的存储位置为下标4。但下标4的位置先前已经被数据4占用了，称数据44的存储位置与数据4发生了冲突，数据44不能再放在下标4的位置上了。

不同的数据元素值通过哈希函数映射到了相同的存储位置，这一现象被称为哈希冲突。

发生哈希冲突的原因之一可能是，哈希函数设计得不够合理。哈希函数设计得越精妙，发生哈希冲突的概率就越低。但无论如何防备，哈希冲突都是无法完全避免的，只能通过一些特殊的方式来解决。

一般来说，闭散列和开散列是解决哈希冲突最常用的两种方法。

2.闭散列

闭散列又称开放定址法。当哈希冲突发生时，若哈希表未被装满，就把数据元素按规则存放到冲突位置中的“下一个” 空位置去（其实就是占用别的数据元素的位置，这样做的缺陷是空间利用率往往较低，但这也是哈希的缺陷，本质上是在以空间换时间）。

而寻找下一个空位置的方法，主要有线性探测和二次探测两种。

2-1.线性探测

从冲突位置开始，依次向后探测，直到寻找到下一个空位置为止。

2-2.二次探测

二次探测是基于线性探测的改良。

线性探测存在的缺陷是，当某一个冲突位置上堆积了许多数据元素，那么线性探测的次数就可能会非常之多。二次探测是将每次向后探测的位置由“1，2，3，4”这样的线性变化，变成“1，4，9，16”这样的非线性变化，使得每次产生哈希冲突后，下一个空位分部散乱，再冲突的可能性降低。

3.闭散列的模拟实现

3-1.基本结构

#include<vector>namespace open_address
{enum STATE //枚举体定义存储位置的状态{EXIST, //存在EMPTY, //为空（即不存在，标记这个位置为可覆盖的）DELETE //被删除（标记这个位置为可覆盖的）};template<class K, class V>struct HashData //数据元素{pair<K, V> _kv;         //数据元素的值STATE _state = EMPTY;   //存储位置的状态（引入状态来更好地管理这个数据元素）};template<class K, class V>class HashTable{public:HashTable() { _table.resize(10); }//构造函数bool Insert(const pair<K, V>& kv); //插入HashData<const K, V>* Find(const K& kv); //查找bool Erase(const K& key); //删除private:vector<HashData<K, V>> _table;//哈希表size_t _n = 0;                    //存储有效数据个数（存放新数据可能涉及扩容，故定义_n）};}

3-2.插入

向哈希表插入一个新的数据元素，既要找到合适的插入位置，又要留意哈希表的容量是否充足，不足则应扩容后再插入。

为了判断哈希表的容量是否充足，前人引入了载荷因子的概念：

【Tips】载荷因子 vs 冲突发生的概率 vs 空间利用率

载荷因子越大，冲突发生的概率越大，空间利用率越高；

载荷因子越小，冲突发生的概率越小，空间利用率越低。

（ps：哈希表不能等空间全满才扩容，也无法等到空间全满才扩容，而是载荷因子到一定值就扩容。下取载荷因子为0.7。）


//这是两个仿函数
template<class K>
struct DefaultHashFunc
{size_t operator()(const K& key){return (size_t)key; //将const K类型的变量转换成整型变量}
};
template<>
struct DefaultHashFunc<string> //这个仿函数是对专门的类型（string）的特化
{size_t operator()(const string& str){// BKDR（字符串哈希函数）：//Q：如何将字符串转化为整型来取模//A：将字符串的每个字符的ASCII码值相加//Q：每个字符相加的ASCII码值相同怎么办？例如，"bacd"、"abcd"、"abbe"等//A：利用BKDR（每个字符相加前，将和*=131后再加字符的ASCII码值）解决冲突size_t hash = 0;for (auto ch : str){hash *= 131;hash += ch;}return hash;}
};
namespace open_address
{//...template<class K,class V, class HashFunc = DefaultHashFunc<K>>class HashTable{//...bool Insert(const pair<K, V>& kv){//step1.检查扩容//if((double)_n/_table.size()>=0.7)if (_n * 10 / _table.size() >= 7) //有效数据个数/表的当前长度>=载荷因子，则需对表扩容{//开辟一个新哈希表size_t newSize = _table.size() * 2; //粗略扩容为旧表长度的2倍HashTable<K, V> newHT;newHT._table.resize(newSize);//遍历旧表，将其重新映射到新表for (size_t i = 0; i < _table.size(); i++){if (_table[i].state == EXIST){newHT.Insert(_table[i]._kv);}}//然后将新表赋给旧表（交换会产生一个随用随弃临时变量，以达到新表赋给旧表的效果）_table.swap(newHT._table); }//step2.线性探测，寻找合适的存放位置HashFunc hf; //仿函数对象size_t hashi = hf(kv.first) % _table.size(); //按除留余数法找到一个哈希地址//ps：//1.const K类型的变量本身是无法取模的，通过仿函数转换为整型后便可取模//2. 模capacity()（空间容量）会有访问越界的隐患，因为_n之后的空间其实是无法访问的。故模.size()（有效数据个数）while (_table[hashi]._state == EXIST) //这个位置存在数据元素，说明这是一共冲突位置{//那就继续往后寻找合适的哈希地址++hashi; hashi %= _table.size();//这里再取模是为了让存放位置始终在哈希表内}//找到后将数据元素放在合适的哈希地址_table[hashi]._kv = kv;       //放值_table[hashi]._state = EXIST; //改状态为存在//放完后增加表的有效数据个数++_n;return true;}//...};
};

3-3.查找和删除


//两个仿函数
template<class K>
struct DefaultHashFunc
{size_t operator()(const K& key){return (size_t)key; //将const K类型的变量转换成整型变量}
};
template<>
struct DefaultHashFunc<string>
{size_t operator()(const string& str){// BKDRsize_t hash = 0;for (auto ch : str){hash *= 131;hash += ch;}return hash;}
};
namespace open_address
{//...template<class K,class V, class HashFunc = DefaultHashFunc<K>>class HashTable{//...//查找HashData<const K, V>* Find(const K& kv){//线性探测HashFunc hf; //仿函数对象size_t hashi = hf(kv) % _table.size();//const K类型的变量本身是无法取模的，通过仿函数转换为整型后便可取模while (_table[hashi]._state != EMPTY) //找到空的位置为止{if (_table[hashi]._state == EXIST        //这个位置存在&& _table[hashi]._kv.first == kv)    //数据的值也符合条件{return (HashData<const K, V>*) & _table[hashi]; //就说明找到了}//没找到就继续往后找++hashi;hashi %= _table.size();}return nullptr;}//删除bool Erase(const K& key){HashData<const K, V>* ret = Find(); //找到要删除的数据if (ret){ret->_state = DELETE; //标记位置为“被删除”--_n;                 //有效数据个数-1return true;}return false;}//...};
};

3-4.完整代码

#include<vector>template<class K>
struct DefaultHashFunc
{size_t operator()(const K& key){return (size_t)key;}
};
template<>
struct DefaultHashFunc<string>
{size_t operator()(const string& str){// BKDRsize_t hash = 0;for (auto ch : str){hash *= 131;hash += ch;}return hash;}
};namespace open_address
{enum STATE{EXIST,EMPTY,DELETE};template<class K, class V>struct HashData{pair<K, V> _kv;STATE _state = EMPTY;};template<class K, class V, class HashFunc = DefaultHashFunc<K>>class HashTable{public:HashTable(){_table.resize(10);}bool Insert(const pair<K, V>& kv){if (_n * 10 / _table.size() >= 7){size_t newSize = _table.size() * 2;/*vector<HashData> newtable;newtable.resize(newSize);*/HashTable<K, V> newHT;newHT._table.resize(newSize);for (size_t i = 0; i < _table.size(); i++){if (_table[i].state == EXIST){newHT.Insert(_table[i]._kv);}}_table.swap(newHT._table);}HashFunc hf;size_t hashi = hf(kv.first) % _table.size();while (_table[hashi]._state == EXIST){++hashi;hashi %= _table.size();}_table[hashi]._kv = kv;_table[hashi]._state = EXIST;++_n;return true;}HashData<const K, V>* Find(const K& kv){if (Find(kv.first)){return false;}HashFunc hf;size_t hashi = hf(kv) % _table.size();while (_table[hashi]._state != EMPTY){if (_table[hashi]._state == EXIST&& _table[hashi]._kv.first == kv){return (HashData<const K, V>*) & _table[hashi];}++hashi;hashi %= _table.size();}return nullptr;}bool Erase(const K& key){HashData<const K, V>* ret = Find();if (ret){ret->_state = DELETE;--_n;return true;}return false;}private:vector<HashData<K, V>> _table;size_t _n;};}

4.开散列

开散列又称为链地址法、拉链法或哈希桶，从逻辑结构上看像是将一个个链表挂在了一个线性表上。

数据元素通过哈希函数可能得到相同的存储位置，从而引发冲突。闭散列将存储位置相同的数据元素归于一个个称为“桶”的子集，每一个“桶”中的数据元素通过一个单链表链接起来，然后将“桶”（链表）的头节点存储在哈希表中。

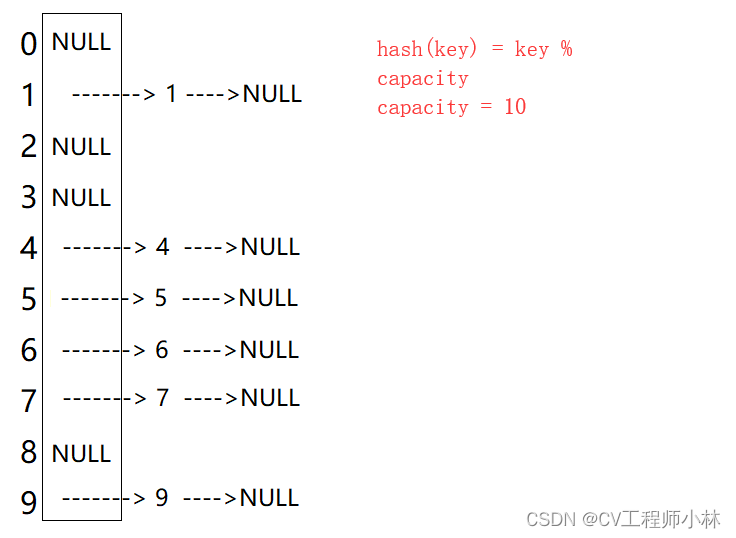
闭散列处理冲突，需要增设链接指针，似乎增加了存储的负担。但事实上，闭散列要求必须保持大量的空闲空间来确保搜索效率，哈希表的每一项所占空间其实比开散列要求的指针大得多，所以开散列反而比闭散列节省空间资源。

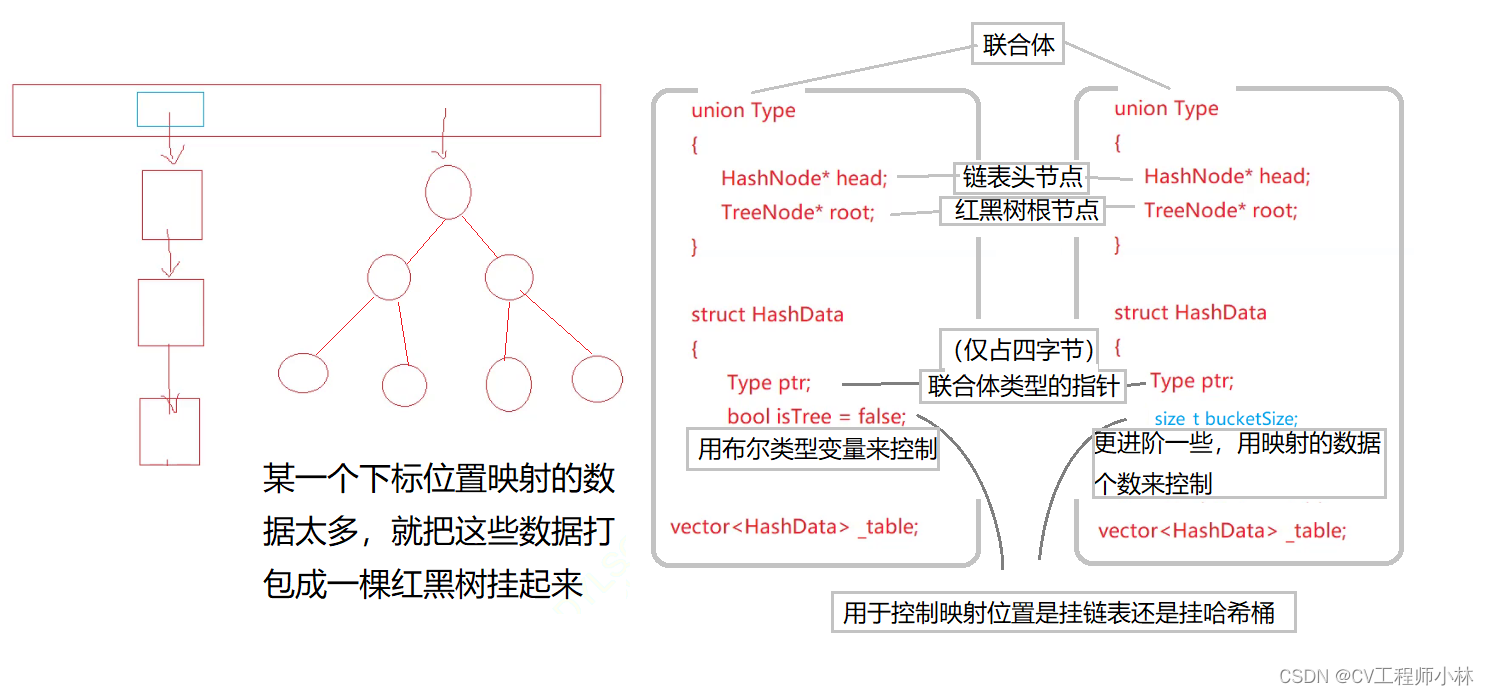
不过，这并不能说明开散列就是完美无缺的。当线性表上挂着的某一条链表太长（也就是说，线性表的某一个下标位置映射的数据太多），也会使搜索效率低下。有一种方案十分巧妙，如果某一个下标位置映射的数据太多，就把这些数据打包成一棵红黑树挂起来。

5.开散列的模拟实现

5-1.基本结构

#include<vector>
namespace hash_bucket
{   //“桶”（链表）节点template<class K, class V>struct HashNode{pair<K, V> _kv;HashNode<K, V>* _next;HashNode(const pair<K, V>& kv):_kv(kv),_next(nullptr){}};//哈希表（哈希桶）template<class K, class V>class HashTable{typedef HashNode<K, V> Node;public:HashTable(){_table.resize(10, nullptr);}private:vector<Node*> _table; // 为了动态地管理数据，哈希表用指针数组来存“桶”（链表）size_t _n = 0;        // 有效数据个数};
}

5-2.查找

//这是两个仿函数
template<class K>
struct DefaultHashFunc
{size_t operator()(const K& key){return (size_t)key;}
};template<>
struct DefaultHashFunc<string> //特化
{size_t operator()(const string& str){size_t hash = 0;for (auto ch : str){hash *= 131;hash += ch;}return hash;}
};namespace hash_bucket
{template<class K, class V>struct HashNode{pair<K, V> _kv;HashNode<K, V>* _next;//...};template<class K, class V, class HashFunc = DefaultHashFunc<K>>class HashTable{typedef HashNode<K, V> Node;public://...//查找Node* Find(const K& key){HashFunc hf; //仿函数对象//除留余数法寻找数据的哈希地址size_t hashi = hf(key) % _table.size();//找到后，在相应链表中寻找目标数据Node* cur = _table[hashi];while (cur){if (cur->_kv.first == key){return cur;}cur = cur->_next;}return nullptr;}//...};
}

5-3.插入

向哈希表插入一个新的数据元素，首先要找到合适的插入位置，也要留意哈希表的容量是否充足，不足则应扩容后再插入，而对于哈希桶而言，通过头插的方式来链接新的数据元素更为简便。

如果不扩容，那么“桶”的个数就是固定的。随着数据元素的不断插入，每个桶中的元素个数会不断增多，可能会导致某一个桶中的链表偏长，从而影响哈希表的搜索性能。因此，在一定条件下需要对哈希表进行扩容。

对于是否扩容的判断，与闭散列类似，引入了载荷因子。但与闭散列不同的是，开散列的载荷因子设为了1。不扩容，不断插入，会使某些“桶”越来越长，让哈希表的搜索性能得不到保障，因此载荷因子应适当大一些（一般控制在1，即在元素个数恰好等于表长/“桶”的个数时，给哈希表扩容），使哈希表在理想情况下，平均每一个“桶”中都有一个数据元素。

//这是两个仿函数
template<class K>
struct DefaultHashFunc
{size_t operator()(const K& key){return (size_t)key;}
};template<>
struct DefaultHashFunc<string> //特化
{size_t operator()(const string& str){size_t hash = 0;for (auto ch : str){hash *= 131;hash += ch;}return hash;}
};namespace hash_bucket
{template<class K, class V>struct HashNode{pair<K, V> _kv;HashNode<K, V>* _next;//...};template<class K, class V, class HashFunc = DefaultHashFunc<K>>class HashTable{typedef HashNode<K, V> Node;public://...//插入bool Insert(const pair<K, V>& kv){//待插入数据在表中已经存在，就不需要插入了if(Find(kv.first)){return false;}//扩容HashFunc hf; //仿函数对象if (_n == _table.size()) //载荷因子到1就扩容{   //开一个新哈希表size_t newSize = _table.size()*2;//此处默认扩容2倍vector<Node*> newTable;          newTable.resize(newSize, nullptr);//遍历旧表，将节点（指针）逐个迁到新表中for (size_t i = 0; i < _table.size(); i++){Node* cur = _table[i];while (cur){Node* next = cur->_next; //暂存一下cur的下一个节点//除留余数法确定新的哈希地址size_t hashi = hf(cur->_kv.first) % newSize; // 将旧表桶中的数据（在旧的哈希地址下）头插到新表的桶中（在新的哈希地址下）cur->_next = newTable[hashi];//旧表数据的next指针指向新表中桶的头节点newTable[hashi] = cur;       //将刚头插的节点置为新表中桶的头节点指针cur = next; //向后移动，处理下一个数据}_table[i] = nullptr; //别忘了每次要将旧表的桶置空，以防内存泄漏}//然后，交换新表和旧表，以达到新替旧_table.swap(newTable);}//插入size_t hashi = hf(kv.first) % _table.size(); //用除留余数法找哈希地址// 找到后将待插入元素头插在“桶”（链表）中Node* newnode = new Node(kv);newnode->_next = _table[hashi];// 然后将头插的新节点置为哈希表中所存的链表的头节点指针_table[hashi] = newnode;++_n;return true;}//...};
}

5-4.删除

//这是两个仿函数
template<class K>
struct DefaultHashFunc
{size_t operator()(const K& key){return (size_t)key;}
};template<>
struct DefaultHashFunc<string> //特化
{size_t operator()(const string& str){size_t hash = 0;for (auto ch : str){hash *= 131;hash += ch;}return hash;}
};namespace hash_bucket
{template<class K, class V>struct HashNode{pair<K, V> _kv;HashNode<K, V>* _next;//...};template<class K, class V, class HashFunc = DefaultHashFunc<K>>class HashTable{typedef HashNode<K, V> Node;public://...//删除bool Erase(const K& key){HashFunc hf; //仿函数对象//除留余数法确定数据在表中的哈希地址size_t hashi = hf(key) % _table.size();//确定后，在相应链表中寻找要删除的数据Node* prev = nullptr;     //前驱节点Node* cur = _table[hashi];//目标节点while (cur){   //找到了if (cur->_kv.first == key){                    if (prev == nullptr) //是链表的第一个（头）节点就把第二个节点置为新的头节点{_table[hashi] = cur->_next;}else //一般情况，就将cur的前后链接以断开cur{prev->_next = cur->_next;}delete cur; //维护完链表结构，释放cur	return true;}//没找到就继续往后找prev = cur;cur = cur->_next;}return false;//找遍了链表也没找到，删除失败}//...};
}

5-5.特别的析构

因为每个插入的新节点都是通过new开辟的，所以在HashTable对象析构时，它们需在析构函数中手动释放。

//...namespace hash_bucket
{template<class K, class V>struct HashNode{pair<K, V> _kv;HashNode<K, V>* _next;HashNode(const pair<K, V>& kv):_kv(kv),_next(nullptr){}};template<class K, class V, class HashFunc = DefaultHashFunc<K>>class HashTable{typedef HashNode<K, V> Node;public:HashTable(){_table.resize(10, nullptr);}//析构~HashTable(){//将桶（链表）逐个节点地释放，释放完将桶置空for (size_t i = 0; i < _table.size(); i++){Node* cur = _table[i];while (cur){Node* next = cur->_next;delete cur;cur = next;}_table[i] = nullptr;}}//...private:vector<Node*> _table;size_t _n = 0; };
}

5-6.完整代码

#include<vector>
template<class K>
struct DefaultHashFunc
{size_t operator()(const K& key){return (size_t)key;}
};
template<>
struct DefaultHashFunc<string>
{size_t operator()(const string& str){size_t hash = 0;for (auto ch : str){hash *= 131;hash += ch;}return hash;}
};namespace hash_bucket
{template<class K, class V>struct HashNode{pair<K, V> _kv;HashNode<K, V>* _next;HashNode(const pair<K, V>& kv):_kv(kv),_next(nullptr){}};template<class K, class V, class HashFunc = DefaultHashFunc<K>>class HashTable{typedef HashNode<K, V> Node;public:HashTable(){_table.resize(10, nullptr);}~HashTable(){for (size_t i = 0; i < _table.size(); i++){Node* cur = _table[i];while (cur){Node* next = cur->_next;delete cur;cur = next;}_table[i] = nullptr;}}bool Insert(const pair<K, V>& kv){if(Find(kv.first)){return false;}HashFunc hf;if (_n == _table.size()){size_t newSize = _table.size()*2;vector<Node*> newTable;newTable.resize(newSize, nullptr);for (size_t i = 0; i < _table.size(); i++){Node* cur = _table[i];while (cur){Node* next = cur->_next;size_t hashi = hf(cur->_kv.first) % newSize;cur->_next = newTable[hashi];newTable[hashi] = cur;cur = next;}_table[i] = nullptr;}_table.swap(newTable);}size_t hashi = hf(kv.first) % _table.size();Node* newnode = new Node(kv);newnode->_next = _table[hashi];_table[hashi] = newnode;++_n;return true;}Node* Find(const K& key){HashFunc hf;size_t hashi = hf(key) % _table.size();Node* cur = _table[hashi];while (cur){if (cur->_kv.first == key){return cur;}cur = cur->_next;}return nullptr;}bool Erase(const K& key){HashFunc hf;size_t hashi = hf(key) % _table.size();Node* prev = nullptr;Node* cur = _table[hashi];while (cur){if (cur->_kv.first == key){if (prev == nullptr){_table[hashi] = cur->_next;}else{prev->_next = cur->_next;}delete cur;	return true;}prev = cur;cur = cur->_next;}return false;}private:vector<Node*> _table; size_t _n = 0; };
}

三、哈希的应用

1.哈希表

哈希表是一种能够表示“数据元素-存储位置”这种映射关系的数据结构，理论上，任何具有这种映射关系的数据结构都可以当作哈希表来使用。而它们除了可以用于快速查找，也可以用于统计数目。

常见的例如一个整型数组，当中的元素和元素下标具有一定映射关系，可以用于统计某一个英文字符的出现次数（如上文中，直接定址法中的例子）；在这道算法题判定是否互为字符重排

的题目答案中，大小为26的整型数组hash也被用于统计某一个英文字符的出现次数。

//题目答案
class Solution {
public:bool CheckPermutation(string s1, string s2) {if(s1.size()!=s2.size())return false;int hash[26]={0};for(auto ch:s1)hash[ch-'a']++;for(auto ch:s2){hash[ch-'a']--;if(hash[ch-'a']<0)return false;}return true;}
};

另外，一个整型数组也可以用于实现计数排序（详见【数据结构】八种常见排序算法）。

又例如容器map，其对存储的<key,value>键值对进行排序和去重，使其可以支持类似英汉词典的功能。

又例如以哈希桶作为底层的容器unordered_set（该容器详解见：【C++】Unordered_map && Unordered_set），在这道算法题存在重复元素的题目答案中，被用于统计数字出现的次数。

//题目答案
class Solution {
public:bool containsDuplicate(vector<int>& nums) {unordered_set<int> hash;for(auto x:nums){if(hash.count(x))return true;else hash.insert(x);}return false;}
};

2.位图

2-1.原理与应用

快速查找一个数据是十分常见的数据管理操作，但当数据量十分庞大，例如，要在40亿个无序且不重复的无符号整数中，快速判断某一个无符号整数是否存在，此时又该如何处理，保证查找的效率呢？

不难想到，直接遍历这40亿个数来查找，效率是极低的；如果考虑使用哈希表，将40亿个数存储在一张哈希表中，每个数占4个字节的空间，40亿个数就占了160亿字节（大约16GB）的空间，对系统内存的消耗是极大的，一般的电脑很难承受；如果考虑使用搜索树（例如红黑树），同样的，光存储数据就对系统内存就有极大消耗，更别提构建搜索树本身又附带消耗；而如果将数据全都存在磁盘上，进行外排序和二分查找，空间问题解决了，但时间又很缓慢，效率低下。

其实，只判断某一个数“在不在”，未必先要将这40亿个数全部存起来。“在”或“不在”可以简单地看作“1”或“0”，而一个二进制数都是由“1”或“0”组成的，由此不难联想到，一个二进制数的每一位都与这个二进制数的值有关，也相当于是某一个值“在”或“不在”的标识（例如二进制数要转化为十进制数，它的第一位与2^0有关，第二位与2^1有关）。我们可以仿照这一点，来快速查找一个无符号整数。

无符号整数的数据范围是0到2^32-1。那么，我们可以通过2^32个比特位大小的数组（大约512MB，也就是0.5G），然后将40亿个无符号整数通过直接地址法，映射到对应的下标位置（将无符号整数的值当作下标，且第几号下标也与第几个比特位有关），以此来判断其中某一个无符号整数在不在。

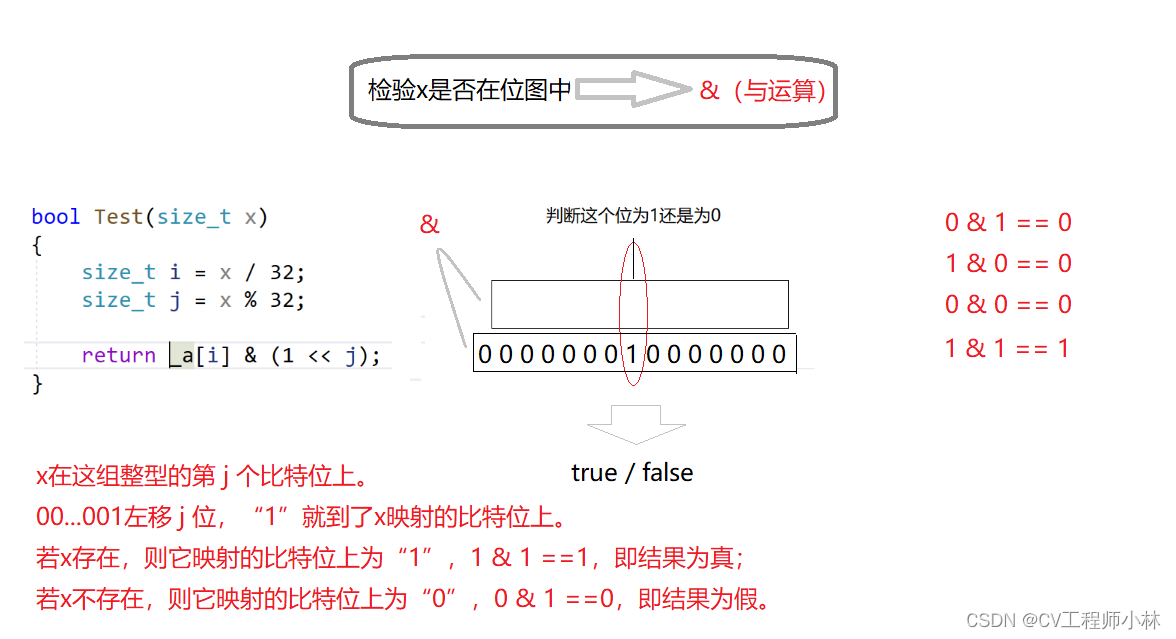
尽管比特位无法作为数组的类型，但我们可以将整型作为数组的类型，并将每一个有32个比特位的整型当作一个组来管理比特位。数组的0号下标存放第一组整型，管理的是第0个到第31个比特位，数组的1号下标存放第二组整型，管理的是第32个到第63个比特位......以此类推。要查询某一个数据的“在”或“不在”的状态，只需确定它映射在数组中的哪一个比特位上；要确定它映射在数组中的哪一个比特位上，只需先确定它映射在第几组整型（即它对应的数组下标是几号），再确定它映射在这组整型的第几个比特位上即可。

像这样的一个数组——涉及位操作，数组下标与某一个数据有映射关系（一般是直接定址法）、与第几个比特位有关，数组元素仅为1和0、用于表示这个数据“在”或“不在”的状态——就是位图。

位图常见的应用情景有：1)快速查找某个数据是否在一个集合中；2)排序 + 去重；3)求两个集合的交集、并集；4)操作系统中磁盘块标记......等等。

C++库中提供了一个容器bitset，它就是位图，常见的操作有访问、计数、查询、修改等。

2-2.模拟实现

namespace CVE
{template<size_t N> //指定位图的大小（bitset< > bt;),N是比特位的数量class bitset{public://构造函数为整型数组申请空间bitset(){_a.resize(N / 32 + 1); //N/32得到整型的数量，+1多申请一个整型以防越界访问（虽然有空间浪费）}// 把x映射的比特位标记成1void set(size_t x){size_t i = x / 32; //先确定x映射在第几组整型（即x对应的数组下标是几号）size_t j = x % 32; //再确定x映射在这组整型的第几个比特位上_a[i] |= (1 << j); //把x映射的比特位标记成1}// 把x映射的比特位标记成0void reset(size_t x){size_t i = x / 32;    //先确定x映射在第几组整型（即x对应的数组下标是几号）size_t j = x % 32;    //再确定x在这组整型的第几个比特位上_a[i] &= (~(1 << j)); //把x映射的比特位标记成0}// 检验x是否在位图中bool test(size_t x){size_t i = x / 32;         //先确定x映射在第几组整型（即x对应的数组下标是几号）size_t j = x % 32;         //再确定x映射在这组整型的第几个比特位上return _a[i] & (1 << j);   //检验x是否在位图中} private:vector<int> _a; //整型数组};
}

3.布隆过滤器

3-1.原理与应用

1970年，Burton Howard Bloom提出了一种紧凑型的、比较巧妙的概率型数据结构，它被称为布隆过滤器。它的特点是可以高效地插入和查询，可以告知用户 “某样东西一定不存在或者可能存在”。它通过多个哈希函数，将一个数据映射到位图中，此种方式不仅可以提升查询效率，也可以节省大量的内存空间。

面对海量数据，尽管位图有十分出色的表现，但是它仍然存在局限，就是它只能映射整型的数据，而无法处理浮点型、字符串。要解决这个问题，可以仿照上文中闭散列、开散列处理字符串映射的方式，先将浮点型、字符串转换成整型再映射。而这就是布隆过滤器的大致原理。

位图映射的是整型，一个值映射一个位置。但字符串的组合无穷之多，冲突的几率很大，所以，布隆过滤器采取了“一个值映射多个位置”的方式，以此来降低冲突的几率。

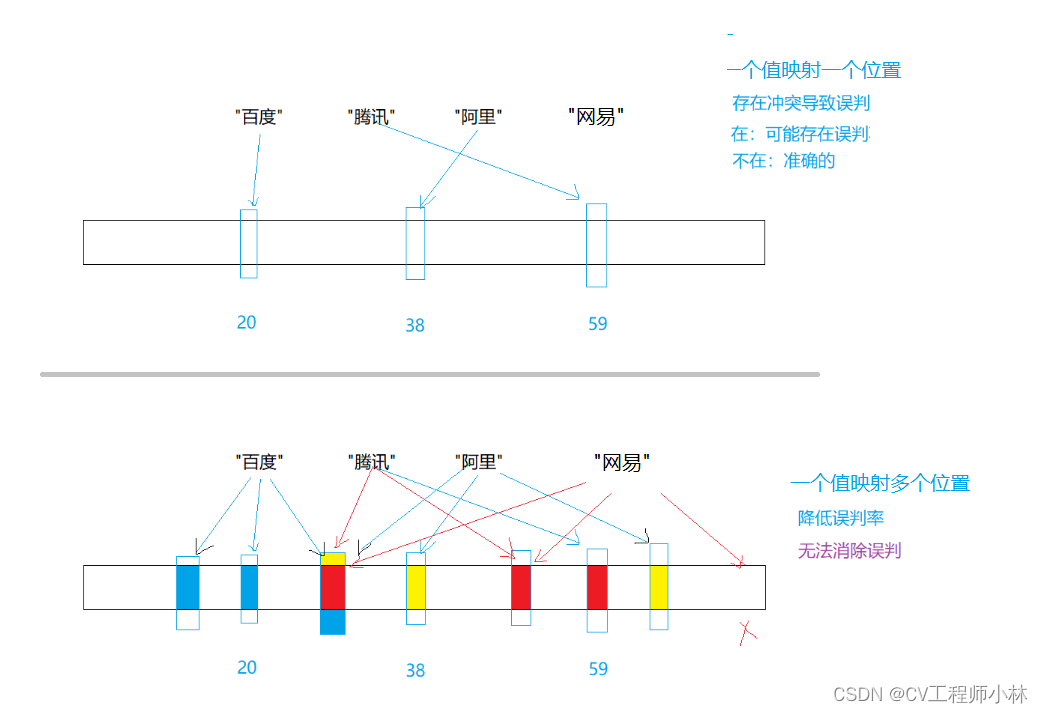
但，布隆过滤器仍存在误判的可能。检验一个字符串是否存在于某个集合，先要将这个字符串通过多个哈希函数转换成的多个数组下标，然后再检验这些下标位置上的值。只有这些下标位置都存的是“1”，才说明这个字符串是存在的，如果其中一个下标是“0”，就说明这个字符串不存在。而万一别的字符串也映射过这些下标，那下标位置上存的就可能都是“1”了。
所以，布隆过滤器判断“一个字符串存在”是可能失误的，但判断“一个字符串不存在”却是始终准确的。

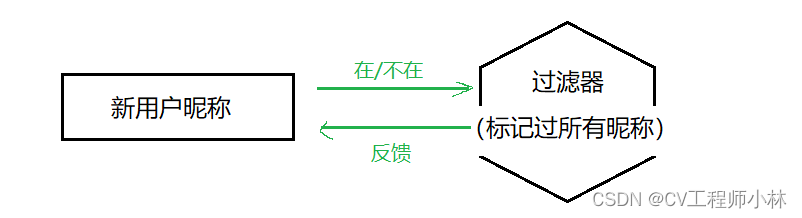
它的应用情景例如，在新用户注册时快速判断一个昵称是否被注册过。在不追求精确的时候，布隆过滤器可以直接告诉用户昵称可不可以用。

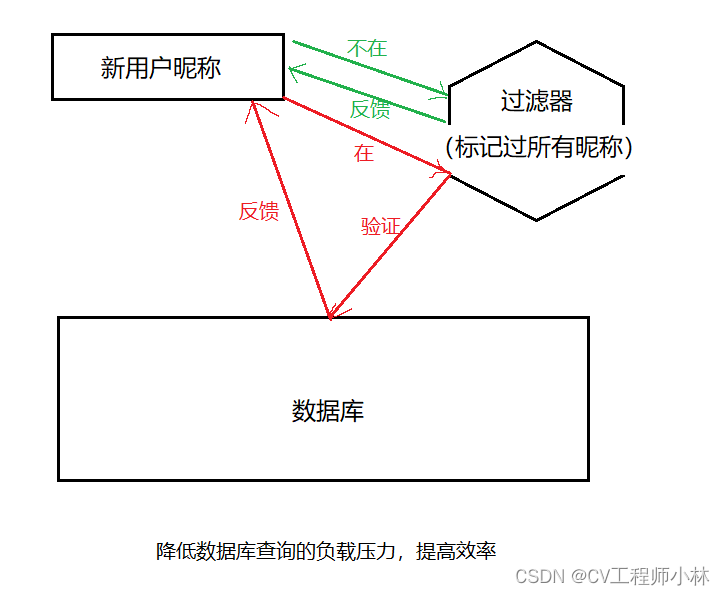
在追求精确的时候，布隆过滤器可以过滤掉“不在”的昵称，剩下“在”的昵称可以进一步到数据库中查验。

如果一个数据被布隆过滤器判断为是不存在，就可以直接告诉用户昵称不可用，要重新想一个昵称；如果被判断为是存在的，再去数据库中查验。这样既保证了判断的准确性，又可以节省了部分去数据库查找的开销（因为数据库在磁盘上，数据读取效率较低，频繁调度开销较大）。

3-2.模拟实现

（关于各种字符串哈希函数的详解，见：字符串哈希算法；关于哈希函数个数、布隆过滤器长度与误判率之间的关系，见：详解布隆过滤器的原理，使用场景和注意事项）

#include<string>
#include<vector>namespace CVE
{//位图template<size_t N>class bitset{public:bitset(){_a.resize(N / 32 + 1);}void set(size_t x){size_t i = x / 32;size_t j = x % 32;_a[i] |= (1 << j);}void reset(size_t x){size_t i = x / 32;size_t j = x % 32;_a[i] &= (~(1 << j));}bool test(size_t x){size_t i = x / 32;size_t j = x % 32;return _a[i] & (1 << j);}private:vector<int> _a;};//以下是三个仿函数//字符串哈希函数1 - BKDR
struct BKDRHash
{size_t operator()(const string& str){size_t hash = 0;for (auto ch : str){hash = hash * 131 + ch;}return hash;}
};//字符串哈希函数2 - AP
struct APHash
{size_t operator()(const string& str){size_t hash = 0;for (size_t i = 0; i < str.size(); i++){size_t ch = str[i];if ((i & 1) == 0){hash ^= ((hash << 7) ^ ch ^ (hash >> 3));}else{hash ^= (~((hash << 11) ^ ch ^ (hash >> 5)));}}return hash;}
};//字符串哈希函数3 - DJB
struct DJBHash
{size_t operator()(const string& str){size_t hash = 5381;for(auto ch : str){hash += (hash << 5) + ch;}return hash;}
};//布隆过滤器
template<size_t N, class K = string,class Hash1 = BKDRHash,class Hash2 = APHash,class Hash3 = DJBHash>
class BloomFilter
{
public://将key映射的多个比特位标记为1void Set(const K& key){//先取映射的下标，再调用位图的接口去标记size_t hash1 = Hash1()(key) % N; //Hash1()是一个匿名的仿函数对象，以下同理_bs.set(hash1);size_t hash2 = Hash2()(key) % N;_bs.set(hash2);size_t hash3 = Hash3()(key) % N;_bs.set(hash3);}//检验key是否存在bool Test(const K& key){//三个映射的比特位但凡有一个存的是0，就说明key不存在size_t hash1 = Hash1()(key) % N;if (_bs.test(hash1) == false)return false;size_t hash2 = Hash2()(key) % N;if (_bs.test(hash2) == false)return false;size_t hash3 = Hash3()(key) % N;if (_bs.test(hash3) == false)return false;//三个映射的比特位放的都是1，才说明key可能存在return true; }private:bitset<N> _bs; //基于位图实现
};}

ps：因为删除一个值的标记可能影响其他值，所以布隆过滤器一般不支持删除。

补、海量数据问题

1.位图相关

问题1：给定100亿个整数，请设计算法找到只出现一次的整数。

解法1：用两个比特位来标记，00表示数不存在，01表示数出现一次，10表示数出现2次。

解法2：优化解法1，通过两个位图来查找。只出现一次的整数在两个位图中，相应比特位上为一个为“0”、另一个为“1”，这样，只需找到“0”、“1”组合的比特位。

#include<vector>namespace CVE
{//位图template<size_t N>class bitset{public:bitset(){_a.resize(N / 32 + 1);}void set(size_t x){size_t i = x / 32;size_t j = x % 32;_a[i] |= (1 << j);}void reset(size_t x){size_t i = x / 32;size_t j = x % 32;_a[i] &= (~(1 << j));}bool test(size_t x){size_t i = x / 32;size_t j = x % 32;return _a[i] & (1 << j);}private:vector<int> _a;};//双位图template<size_t N>class twobitset{public:// 把x映射的比特位标记成1void set(size_t x){// x不存在（位图1中为0，位图2中也为0），即为00，改00为01if (!_bs1.test(x) && !_bs2.test(x)){_bs2.set(x); //将位图2中的比特位标记为1} // x存在一次（位图1中为0，位图2中为1），即为01，改01为10else if (!_bs1.test(x) && _bs2.test(x)){_bs1.set(x);   //将位图1中的比特位标记为1_bs2.reset(x); //将位图2中的比特位标记为0}}// 检验x是否只出现一次bool is_once(size_t x){return !_bs1.test(x) && _bs2.test(x); //x存在一次（位图1中为0，位图2中为1），即为01}private:bitset<N> _bs1; //位图1bitset<N> _bs2; //位图2};
}

双位图代码的测试结果：

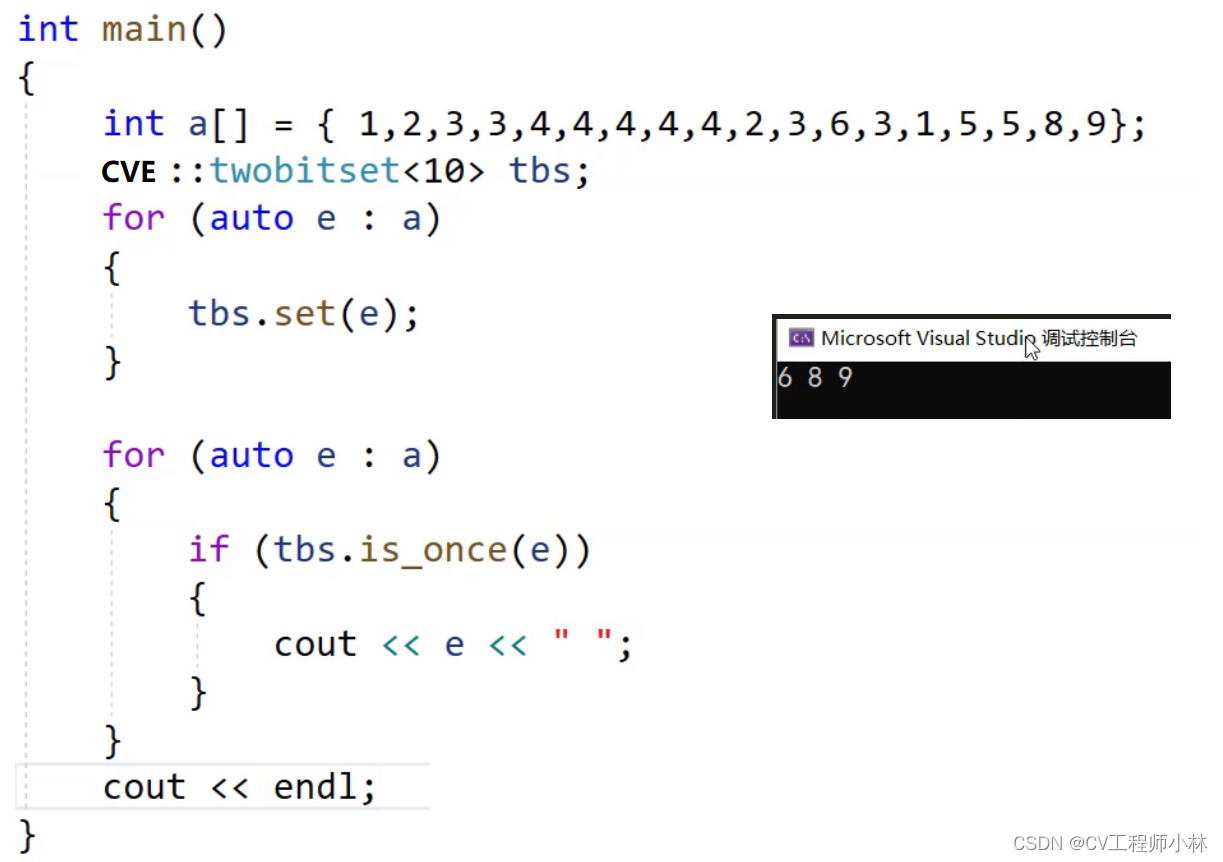
问题2：给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件的交集？

解法：将两个文件的数据分别映射到两个位图，对应位置都为1，那这个位置映射的数据就是交集之一。将两个位图的对应位置&（与运算）一下，得出的结果去重后，就得到两个文件的交集。

#include<vector>namespace CVE
{//位图template<size_t N>class bitset{public:bitset(){_a.resize(N / 32 + 1);}void set(size_t x){size_t i = x / 32;size_t j = x % 32;_a[i] |= (1 << j);}void reset(size_t x){size_t i = x / 32;size_t j = x % 32;_a[i] &= (~(1 << j));}bool test(size_t x){size_t i = x / 32;size_t j = x % 32;return _a[i] & (1 << j);}private:vector<int> _a;};
}

位图代码的测试结果：

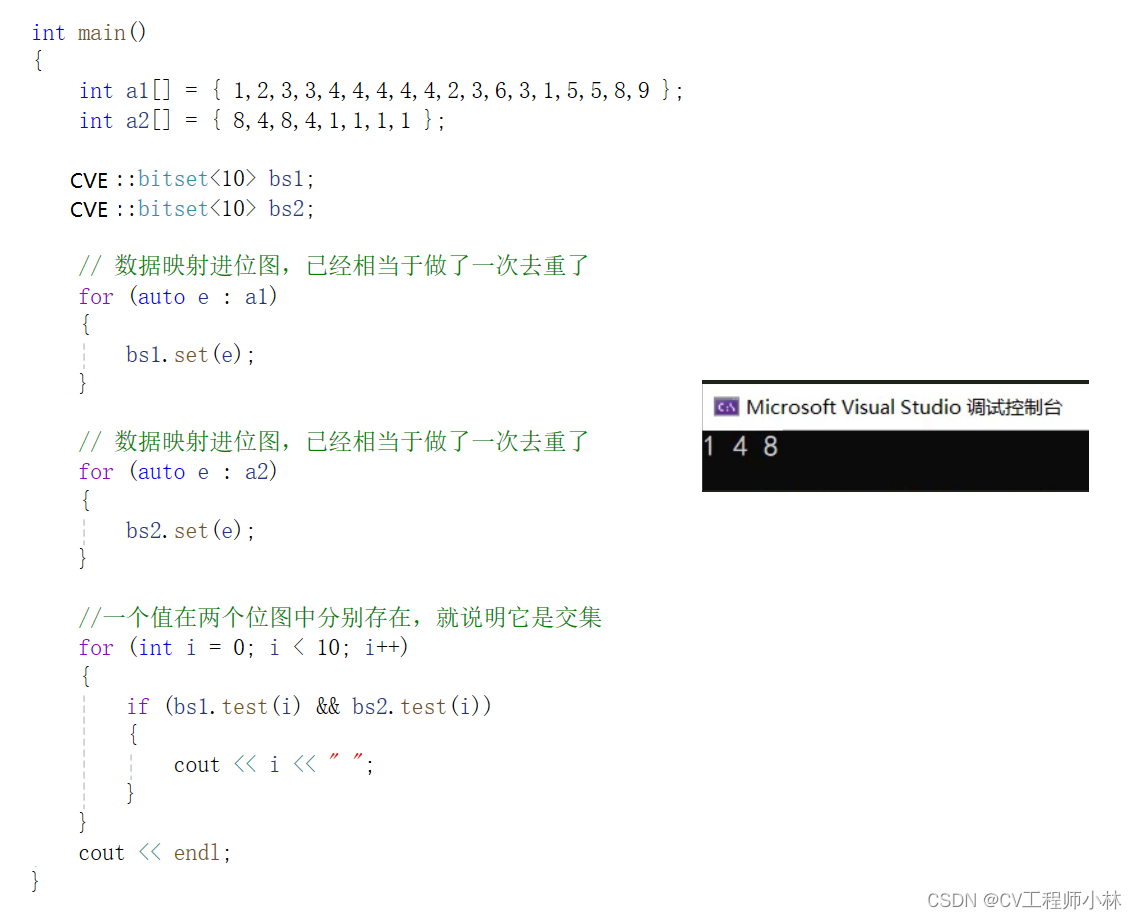
问题3：某1个文件有100亿个int，我们只有1G内存，请设计算法找到出现次数不超过2次的所有整数。

解法：类似问题1，通过两个位图来查找。00表示数不存在，01表示数出现一次，10表示数出现2次，11表示数出现2次以上。

#include<vector>namespace CVE
{//位图template<size_t N>class bitset{public:bitset(){_a.resize(N / 32 + 1);}void set(size_t x){size_t i = x / 32;size_t j = x % 32;_a[i] |= (1 << j);}void reset(size_t x){size_t i = x / 32;size_t j = x % 32;_a[i] &= (~(1 << j));}bool test(size_t x){size_t i = x / 32;size_t j = x % 32;return _a[i] & (1 << j);}private:vector<int> _a;};//双位图template<size_t N>class twobitset{public:void set(size_t x){// x原先不存在，00->01if (!_bs1.test(x) && !_bs2.test(x)){_bs2.set(x); } // x原先存在一次，01->10else if (!_bs1.test(x) && _bs2.test(x)){_bs1.set(x);   _bs2.reset(x); }// x原先存在两次，10->11else if (_bs1.test(x) && !_bs2.test(x)){_bs2.set(x); }}bool not_more_than_twice(size_t x){return !(_bs1.test(x) && _bs2.test(x)); }private:bitset<N> _bs1; //位图1bitset<N> _bs2; //位图2};
}

双位图代码的测试结果：

2.布隆过滤器相关

问题1：如何扩展布隆过滤器，使得它支持删除元素的操作？

解法：多个比特位标记一个值，并使用引用计数。将布隆过滤器中的每个比特位扩展成一个小的计数器，插入元素时给k个计数器(k个哈希函数计算出的哈希地址)加一，删除元素时，给k个计数器减一，通过多占用几倍存储空间的代价来增加删除操作。

问题2：给定两个文件，分别有100亿个query（数据库的查询语句，可以理解为字符串），我们只有1G内存，如何找到两个文件交集？分别给出近似算法。

解法：通过一个布隆过滤器。将一个文件的数据存入布隆过滤器中，再检查相应的数据在另一个文件中在不在，在的就是交集。

3.哈希切割

哈希切割：把字符串转为整型，然后对一个范围取模，以此把一个庞大的数据集合分为一个一个小份，方便处理。

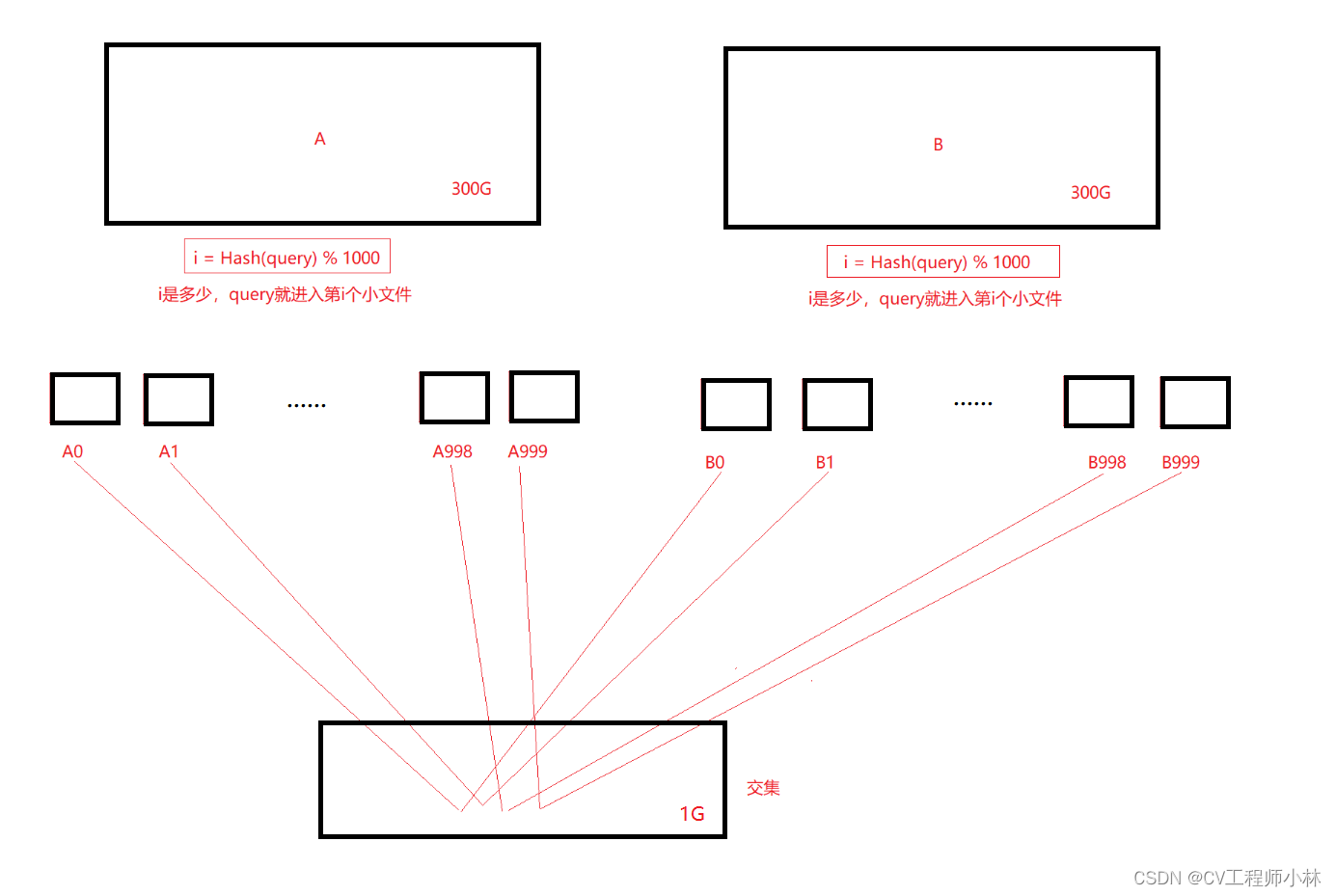
问题1：给定两个文件，分别有100亿个query（数据库的查询语句，可以理解为字符串。100亿个query大约占300G），我们只有1G内存，如何找到两个文件交集？分别给出精确算法。

解法：通过哈希切割，把两个约300G的大文件分成一个一个小份，并给每个小份编号，然后把编号相同的两个小份放入1G内存去找交集。因为映射的缘故，两个大文件中相同的query一定会分别进入编号相同的小份中。

问题2：给定一个超过100G大小的log ﬁle, log中存着IP地址, 如何找到出现次数最多的IP地址？如何找到topK个IP？

解法：哈希切割。先将IP地址映射，然后切分成一个一个小份并依次处理，相同的IP一定进入了同一个小份，此时用map去分别统计每个小份中IP地址出现的次数即可。要找到topK个IP，只需汇总每个小份中，每个IP出现的次数，最后用priority_queue即可获取TopK。