目录

三数取中法选key

优化点

基本思想 

代码实现 

小区间优化

优化点

基本思想

代码实现

---

由于hoare版快排在一些特殊情况下性能并不优，这里我们进行一些优化。 

三数取中法选key

优化点

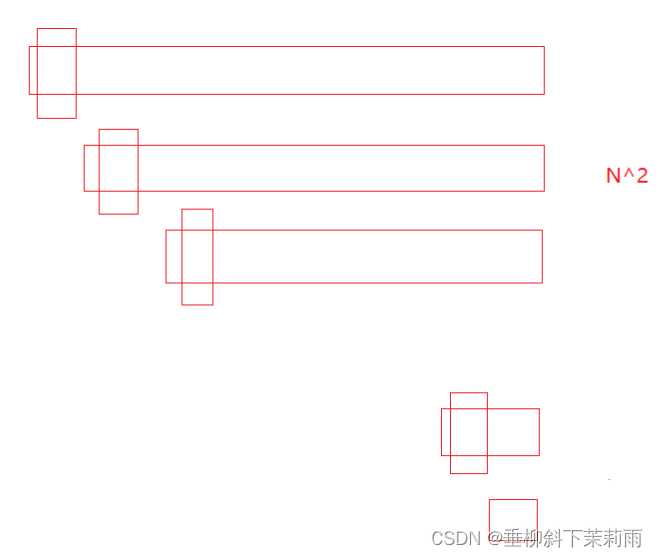
• 当数据有序时，快排就会很吃力，这是为什么呢？

因为有序时，left要找小，right要找大，都找不到，就会一直从头找到尾，时间复杂度就会上升到O(N^2)。在debug版本下，如果数据上万，就会栈溢出。

基本思想 

• 三数取中：取三个数中的中位数下标，选到合适的数，避免选取到最小的最大的数，对顺序结构的效率优化很好。
• 取的是下标❗
• 数值两两比较
• 对快速排序的单趟的优化，三数取中是走快速排序逻辑（每趟的优化）

代码实现 

int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;// begin end midi三个数选中位数if (a[begin] < a[midi]){if (a[midi] < a[end])return midi;else if (a[begin] > a[end])return begin;elsereturn end;}else{if (a[midi] > a[end])return midi;else if (a[begin] < a[end])return begin;elsereturn end;}
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin, right = end;int keyi = begin;while (left < right){// 右边找小while (left < right && a[right] >= a[keyi]){--right;}// 左边找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;// [begin, keyi-1] keyi [keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}

小区间优化

优化点

• 当快排递归到小的子区间时，比如就只有7个数据，我们却还需要再递归7次才能返回结果。没有必要。
• 当数据很少时，用希尔/堆排/快排都很杀鸡用牛刀，这个时候我们只需用直接插入排序即可。

也就是说，当快排递归到小的子区间时，我们考虑使用插入排序，这就是小区间优化。

基本思想

• 主要优化递归层数的最后3~4层
• 最后3~4层的递归层数占据了总的递归层数的80%。

  

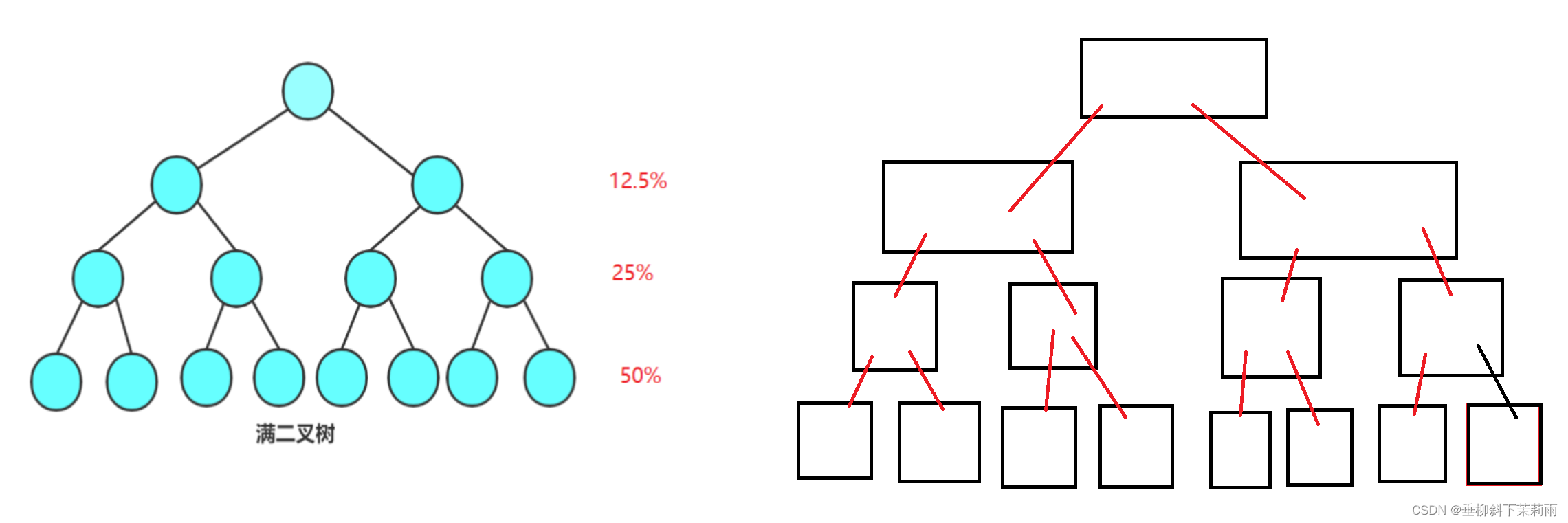
• 区间是[begin，end] ，此区间的数据量是end-begin+1。当数据量end-begin+1<=10的时候，让序列执行直接插入排序
• 每段数据序列被分割了，起始位置并不都是a，要用a+begin表示

代码实现

int GetMidi(int* a, int begin, int end)
{//...
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;if (end - begin + 1 <= 10){InsertSort(a + begin, end - begin + 1);}else{//三数取中的代码...}
}

• 注意：小区间优化在release版本下，并不会与没优化的快多少，因为release已经优化了很多了。

hoare版本总代码

void InsertSort(int* a, int n)
{//[0,end]end+1插入for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (a[end] > tmp){a[end + 1] = a[end];end--;}else{break;}}a[end + 1] = tmp;}
}void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}int GetMidi(int* a, int begin, int end)
{int midi = (begin + end) / 2;// begin midi end 三个数选中位数if (a[begin] < a[midi]){if (a[midi] < a[end])return midi;else if (a[begin] > a[end])return begin;elsereturn end;}else // a[begin] > a[midi]{if (a[midi] > a[end])return midi;else if (a[begin] < a[end])return begin;elsereturn end;}
}int PartSort1(int* a, int begin, int end)
{int midi = GetMidi(a, begin, end);Swap(&a[midi], &a[begin]);int left = begin, right = end;int keyi = begin;while (left < right){// 右边找小while (left < right && a[right] >= a[keyi]){--right;}// 左边找大while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[left], &a[keyi]);keyi = left;return keyi;
}void QuickSort(int* a, int begin, int end)
{if (begin >= end)return;//<10个数字走插入逻辑 if (end - begin + 1 <= 10){InsertSort(a + begin, end - begin + 1);}else{int keyi = PartSort1(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);}
}