K倍区间刷题笔记

法一前缀和暴力搜索（数据大会超时）

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;
const int N=100010;
int a[N],s[N];
int n,k;
int main(){
   cin>>n>>k;
   for(int i=1;i<=n;i++){
       cin>>a[i];
       s[i]=s[i-1]+a[i];
   }
   int cnt=0;
   for(int i=1;i<=n;i++){
       for(int j=1;j<=i;j++){
           int ans=s[i]-s[j-1];
           if(ans%k==0){
               cnt++;
           }
       }
   }
   cout<<cnt;
   return 0;
}`

法二根据式子推导

if((s[i]-s[j-1])%k==0)答案++；

换句话说 s[i]和s[j-1]对k取模的余数是一样的

此处拿样例

5 2

1 2 3 4 5

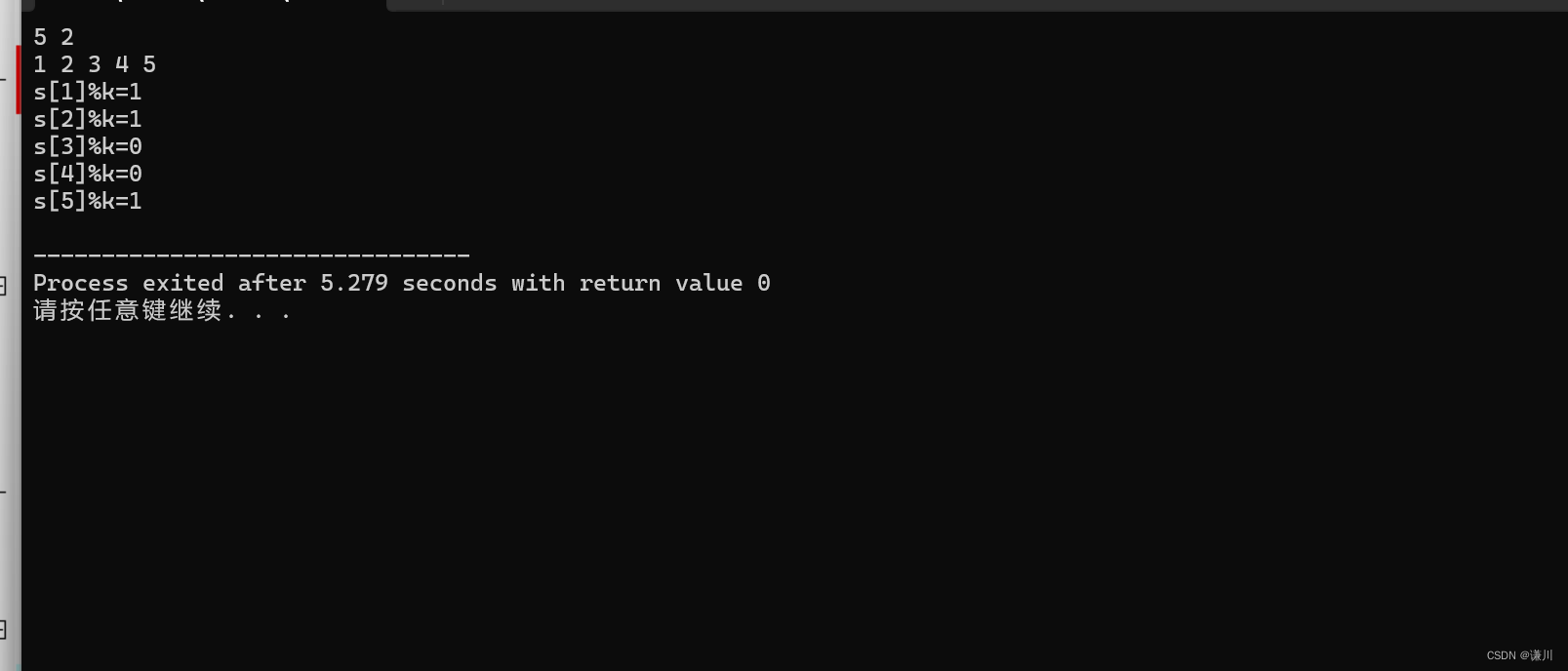
可以看到s1,s2,s5,对k取模的余数是一样的

且s[0]%k=0;

s2和s1，s5和s1,s5和s2能构成三个k倍区间

s3和s0,s4和s0，s4和s3能构成三个k倍区间所以一共六个K倍区间

因此

我们引出开一个cnt数组来记录该余数的出现次数

例如余数2出现了两次说明当前已经有两个s[l-1]对k取模余数为2

后面一旦出现当前余数2 就可以与这两个s[l-1]形成k倍区间

所以答案+上目前余数出现的次数

然后此时余数2已经出现三次则让cnt[2]++;即cnt[2]=3;

将其标记为出现三次后面一旦再出出现余数2的s[r]

答案直接+3 同时将余数2 标记成四次

代码

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
using namespace std;
typedef long long ll;

const int N=100010;
ll a[N],s[N],cnt[N];
ll n,k;
int main(){
   cin>>n>>k;
   for(int i=1;i<=n;i++){
       cin>>a[i];
       s[i]=s[i-1]+a[i];
   }
   ll res=0;
   cnt[0]=1;
   for(int i=1;i<=n;i++){
       res+=cnt[s[i]%k];
       cnt[s[i]%k]++;
   }
   cout<<res;