题目描述
- 给你二叉树的根节点
root,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。
示例1:
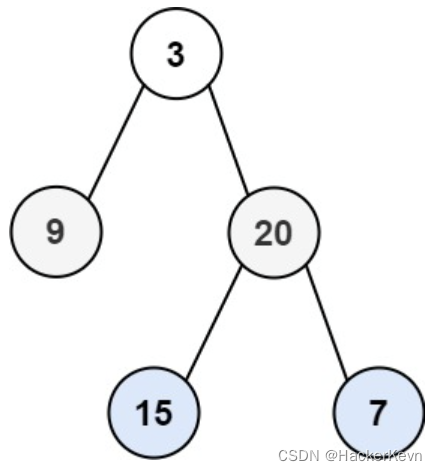
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
示例 2:
输入:root = [1]
输出:[[1]]
示例 3:
输入:root = []
输出:[]
提示:
- 树中节点数目在范围
[0, 2000]内 -1000 <= Node.val <= 1000
思路分析
这个问题实际上可以只用一个队列就实现,只需要再增加一个变量levelSize,用来记录每一层的数据个数,然后再让这个队列一层一层的出去。之前的方法中,实际上队列并不是一层一层出去的,它有可能队列里面同时有两层的数据,我们以下面这个图来解释一下原因:
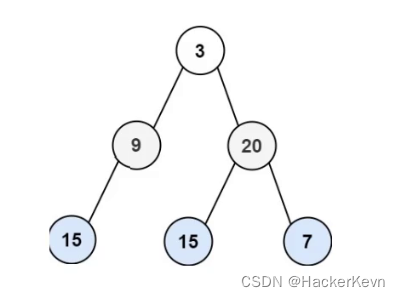
如果有两层队列实现的话,3这个节点出来的时候,会让9和20这两个节点进入队列,而9这个节点出来的时候会让15这个节点进入队列,这个时候队列里面就同时有了第2层和第3层的数据。
所以我们想通过levelSize来达到一个目的:控制这个队列实现一层一层的出去。
那我们要怎么实现呢?我们仍然以刚才的图来进行分析:
3节点进入队列的时候,它的层数为1,由于它是根节点,所以它肯定只有一个,所以3就可以直接出队列。这个时候我们让levelSize进行自减操作它就变成了0,表示这一层已经出完了。
那么由于3节点出的时候会把9和20也带进来,也就是说当前层的节点全部出队列的时候一定是下一层的节点全部进入队列,这个时候我们将levelSize重新更新为第二层节点的数目也就是2,然后再进行出队列的操作:9节点出队列同时将15节点带进队列,然后levelSize自减变为1;20节点出队列同时将15节点和7节点带进队列,levelSize再自减变为0。这个时候就说明第二层也出完了。那么此时第三层都在队列里面所以我们再次更新levelSize的值为3,依次类推直到整棵树都被遍历完就实现了只用一个队列实现层序遍历。
那么根据以上的思路,我们就可以写出下面的代码:
完整代码
class Solution {
public:vector<vector<int>> levelOrder(TreeNode* root) {queue<TreeNode*> q;int levelSize = 0;if (root)//如果根不为空,就入队列{q.push(root);levelSize = 1;}vector<vector<int>> vv;//用来存放一层一层出的节点while (!q.empty())//如果队列不等于空,就说明树还没有被遍历完{//通过levelSize控制一层一层出vector<int> v;//用来存放每一层的数据while (levelSize--)//levelSize是几循环就执行几次,--levelSize表示的则是执行(levelSize - 1)次{TreeNode* front = q.front();//先取队头的数据q.pop();v.push_back(front->val);//进去的同时把该节点的下一层往队列里面带if (front->left)//左如果不为空就让左入队列q.push(front->left);if (front->right)//右如果不为空就让右入队列q.push(front->right);}//走到这里就说明当前层已经出完了,就把当前层所出的数据放到vv里面vv.push_back(v);//更新下一层的数据levelSize = q.size();}return vv;}
};
运行结果


)




)












