一、奇偶性扩展
1、普通轴对称函数
要会根据抽象函数的关系,找出对称轴
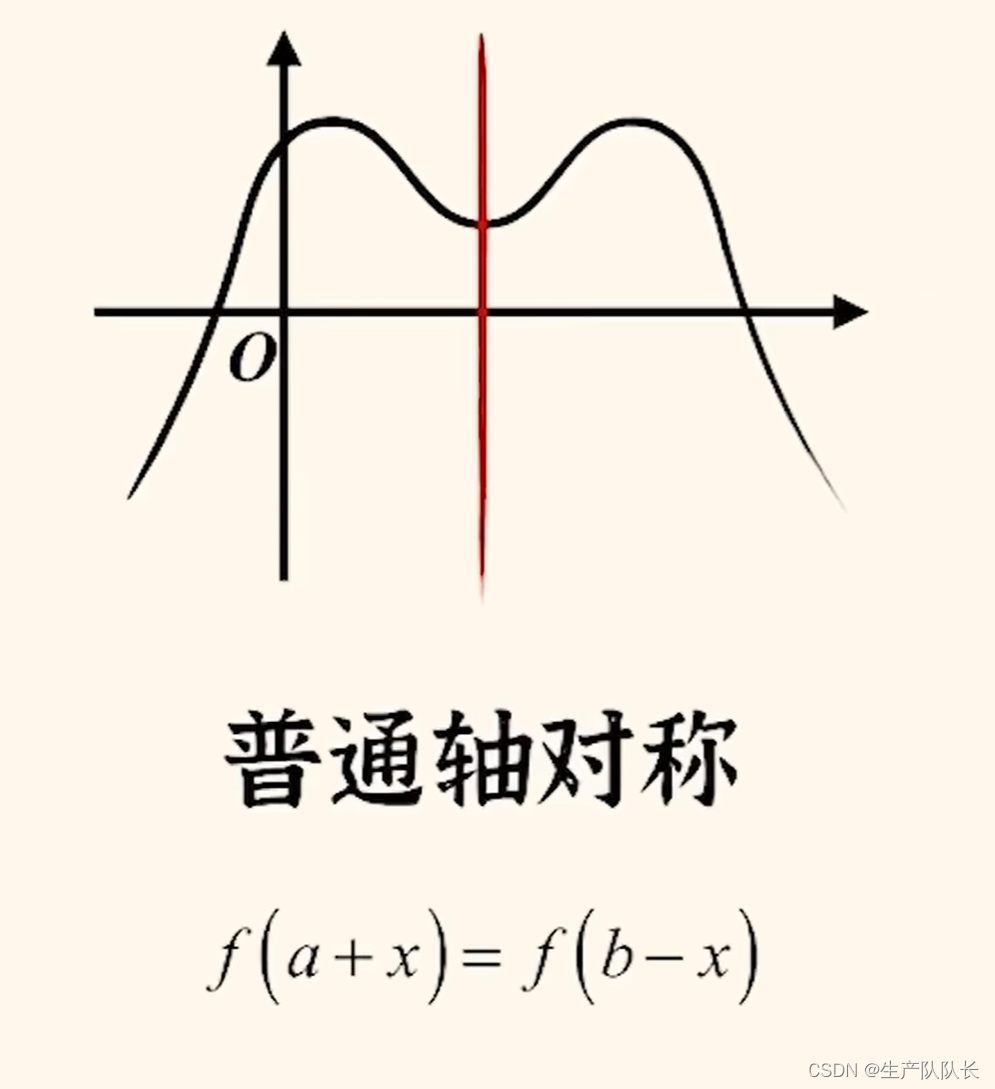
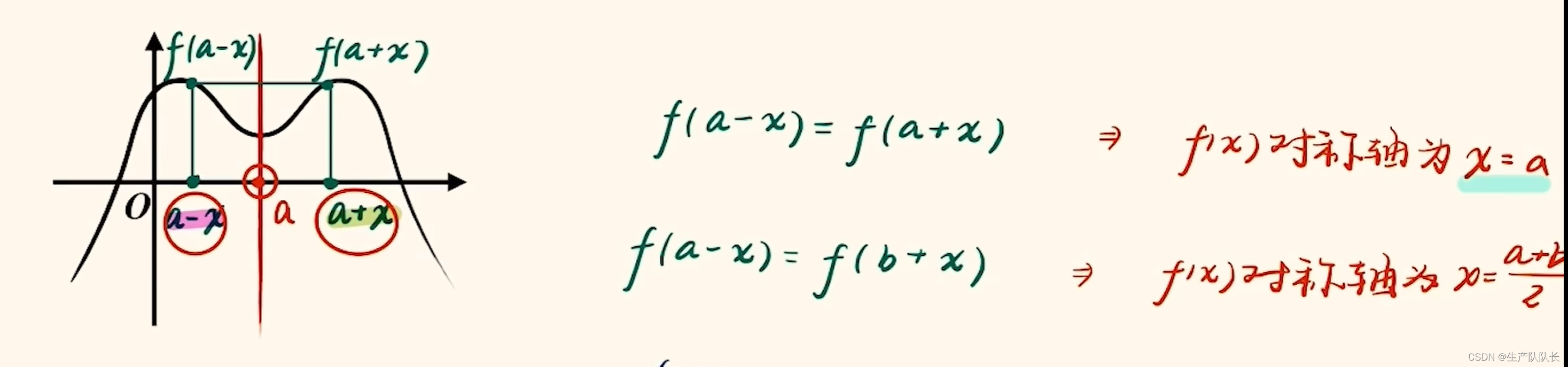
简便记法:纵相等,对称轴
2、普通中心对称函数
要会找出对称中心点坐标
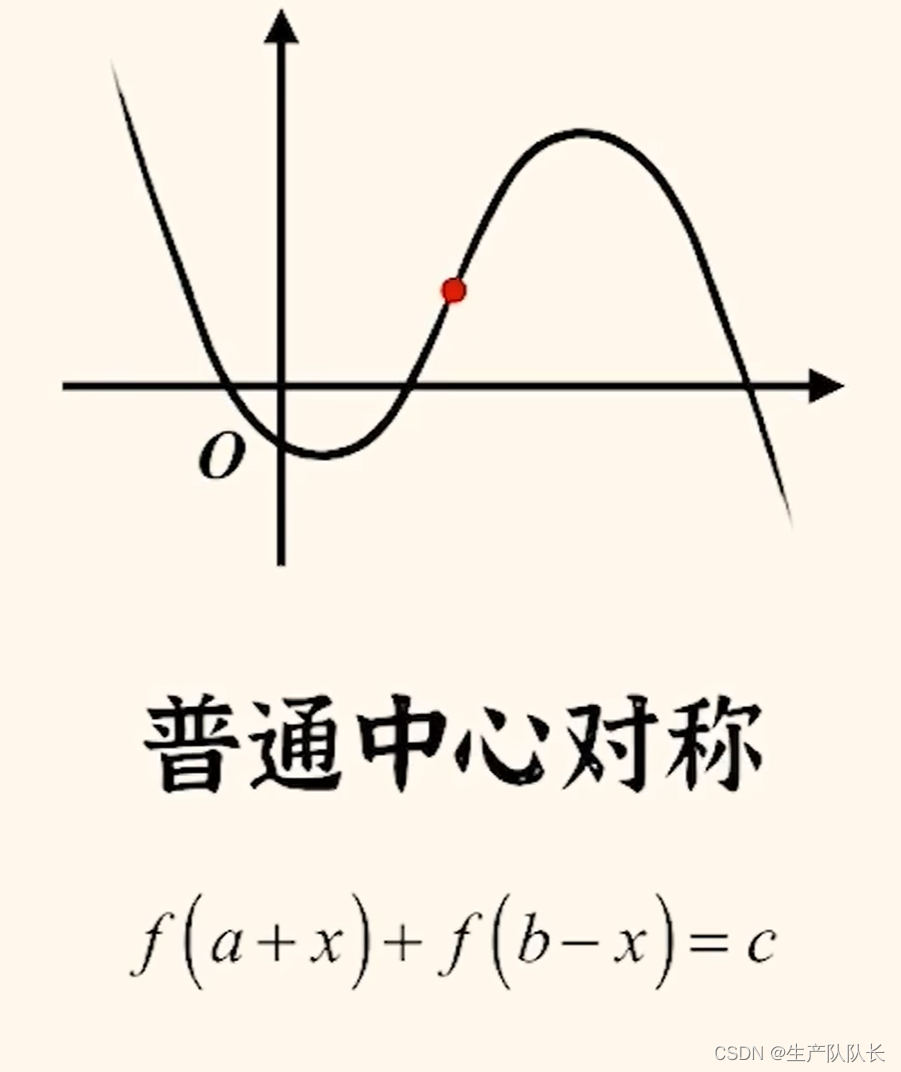
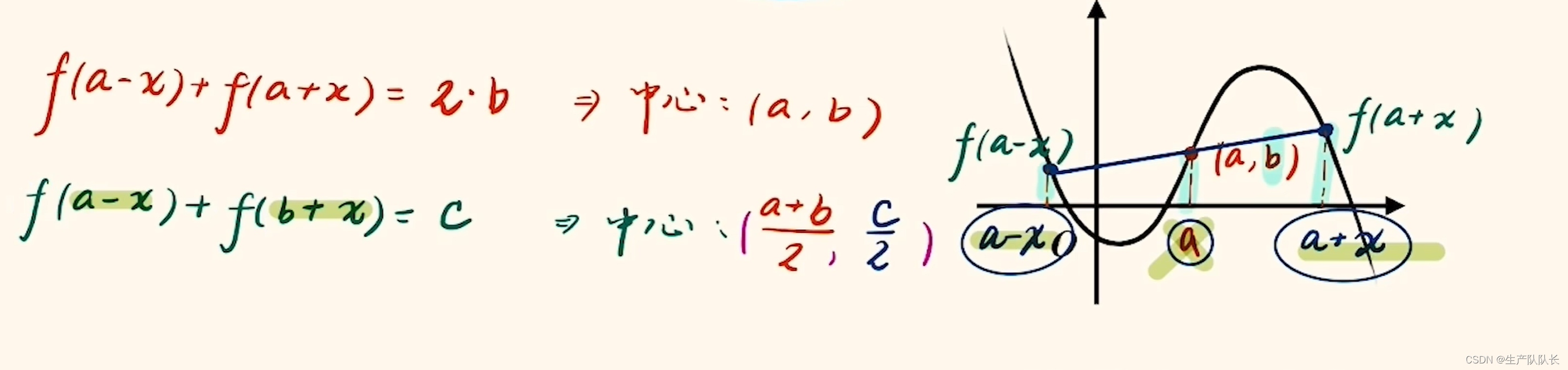
简便记法:纵和定,中心点
二、题型汇总
解题方法
抽象函数
1、定义法
2、画草图分析法
3、根据对称单调性脱f求解法
具体函数
1、判断是轴对称还是中心对称
对函数表达式进行变形(拆分子,因式分解等)
找出对称轴或者对称中心
2、根据对称性求解
3、直接代值消项法
1、对称性
例题1:
直接根据定义式求解

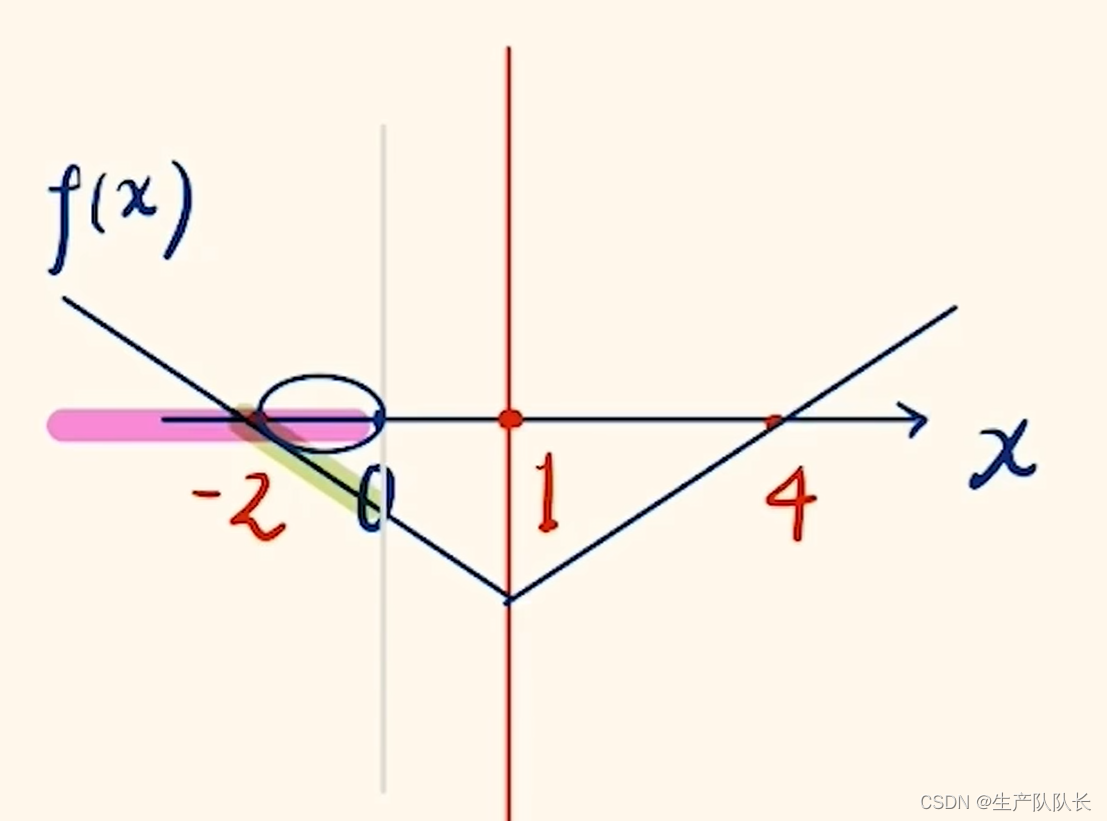
例题2:
1、先根据第一个条件找出对称轴
2、根据第二个条件算出对应点的值
3、根据单调性,画出函数图像
4、分类讨论,求出解集
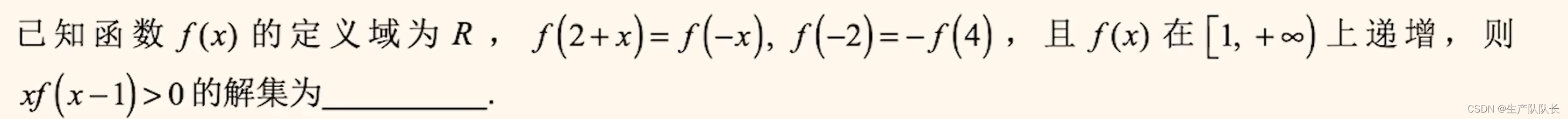

例题3:
1、对函数式变形,找出对称中心
2、根据图像性质求解
或者
直接代值求解
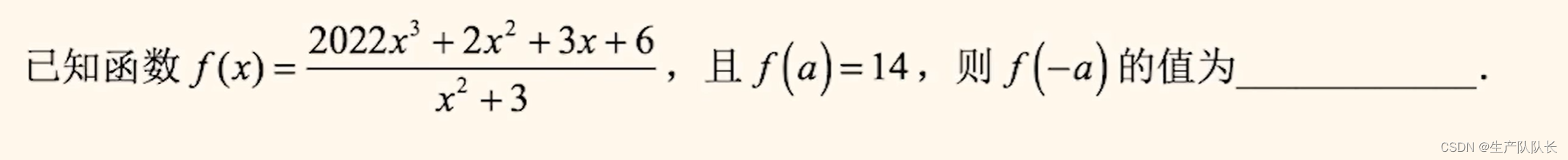
2、利用单调性
直接根据单调性,脱掉f,求解
例题

3、奇函数加单调性
奇函数在对称区间上的单调性相同,以及奇函数的定义-f(x)=f(-x),脱掉f,求解
例题

4、偶函数加单调性
偶函数在对称区间上的单调性相反,根据对称性,x离对称轴越近(用到绝对值),则函数值越大或越小(看图像开口方向),脱掉f,求解
例题
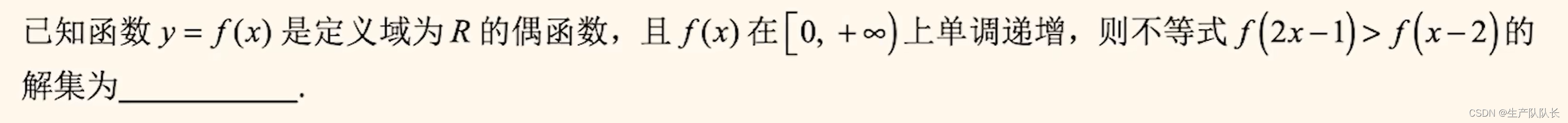



 常用布局)














![Sqli-labs靶场第15关详解[Sqli-labs-less-15]自动化注入-SQLmap工具注入](http://pic.xiahunao.cn/Sqli-labs靶场第15关详解[Sqli-labs-less-15]自动化注入-SQLmap工具注入)
