堆以及堆的实现

文章目录

堆的概念
堆的实现
- HeapPush
- HeapPop
HeapTop HeapSize HeapEmpty
堆的应用

堆的概念

堆是一颗完全二叉树
每个结点的值都小于子结点的值，这颗二叉树为小根堆
每个结点的值都大于子结点的值，这颗二叉树为大根堆
堆的定义如下：n个元素的序列{k1,k2,ki,…,kn}当且仅当满足下关系时，称之为堆。

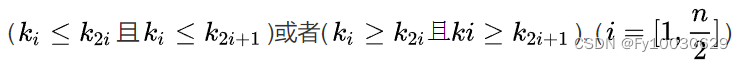
堆的性质
堆中某个节点的值总是不大于或不小于其父节点的值；
堆总是一棵完全二叉树。

堆的实现

在讲堆的实现前，我们首先要知道堆需要实现的功能。

HeapPush
HeapPop(删除根结点)
HeapTop
HeapSize
HeapEmpty
接下来我们要先创建和销毁一个堆。

typedef int HeapType;
typedef struct Heap
{HeapType* arr;int size;int capacity;
}Hp;
void HeapInit(Hp* php)
{assert(php);php->arr = NULL;php->capacity = php->size = 0;
}
void HeapDestroy(Hp* php)
{assert(php);free(php->arr);php->arr = NULL;php->capacity = php->size = 0;
}

HeapPush

实现HeapPush时难点在于如何保持整体是一个堆。
即在一个堆的后面插入一个值，那么这棵完全二叉树大概率不会是堆，那么我们需要将这个值和其父结点比较，再根据需要交换值，也就是AdjustUp。
那么接下来以小根堆为例，实现HeapPush。

void Swap(HeapType* a, HeapType* b)
{HeapType tmp = *a;*a = *b;*b = tmp;
}
void AdjustUp(HeapType* arr, int child)
{int parent = (child - 1) / 2;while (child>0){if (arr[child] < arr[parent]){Swap(&arr[child], &arr[parent]);child = parent;parent = (child - 1) / 2;}else{break;}}
}
void HeapPush(Hp* php, HeapType x)
{assert(php);if (php->size == php->capacity){int newcapacity = (php->capacity == 0 ? 4 : 2 * php->capacity);HeapType * tmp = (HeapType*)realloc(php->arr,newcapacity * sizeof(HeapType));if (!tmp){perror("realloc fail!");exit(-1);}php->arr = tmp;php->capacity = newcapacity;}php->arr[php->size] = x;php->size++;AdjustUp(php->arr, php->size - 1);
}

HeapPop

实现HeapPop也是和HeapPush一样，需要考虑的是如何维持整体完全二叉树是一个堆，由于我们删除的是根结点，如果将根结点的子结点向上调整，那么整体二叉树就会空出一个位置，导致变成非完全二叉树。
这里的解决办法是将根结点和最后一个结点交换，删除最后一个结点，然后再对根结点进行向下调整。

void AdjustDown(HeapType* a, int n, int parent)
{int child = 2 * parent + 1;while (child<n){if (child + 1 < n && a[child] > a[child + 1]){child++;}if (a[parent] > a[child]){Swap(&a[child], &a[parent]);parent = child;child = 2 * parent - 1;}else{break;}}
}
void HeapPop(Hp* php)
{assert(php);assert(php->size);Swap(&php->arr[0], &php->arr[php->size - 1]);php->size--;AdjustDown(php->arr, php->size, 0);
}

HeapTop HeapSize HeapEmpty

实现了Heap的Push和Pop后，那么取根结点的值和判空、判满也是手到擒来的。

HeapType HeapTop(Hp* php)
{assert(php);assert(php->size);return php->arr[0];
}
size_t HeapSize(Hp* php)
{assert(php);return php->size;
}
bool HeapEmpty(Hp* php)
{assert(php);return php->size == 0;
}