活动 - AcWing
深海资源考察探险队的潜艇将到达深海的海底进行科学考察。
潜艇内有多个深海机器人。
潜艇到达深海海底后,深海机器人将离开潜艇向预定目标移动。
深海机器人在移动中还必须沿途采集海底生物标本。
沿途生物标本由最先遇到它的深海机器人完成采集。
每条预定路径上的生物标本的价值是已知的,而且生物标本只能被采集一次。
本题限定深海机器人只能从其出发位置沿着向北或向东的方向移动,而且多个深海机器人可以在同一时间占据同一位置。若机器人不能到达终点则不能放置。
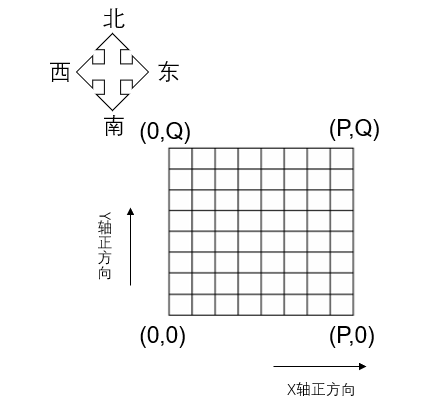
用一个 P×Q 网格表示深海机器人的可移动位置。
西南角的坐标为 (0,0),东北角的坐标为 (P,Q)。
给定每个深海机器人的出发位置和目标位置,以及每条网格边上生物标本的价值。
计算深海机器人的最优移动方案,使尽可能多的深海机器人到达目的地的前提下,采集到的生物标本的总价值最高。
输入格式
第 1 行为深海机器人的出发位置数 a,和目的地数 b,第 2 行为 P 和 Q 的值。
接下来的 P+1 行,每行有 Q 个正整数,其中第 i 行(从 0 开始计数)的第 j 个(从 0 开始计数)正整数表示点 (i,j) 到点 (i,j+1) 的路径上生物标本的价值。
再接下来的 Q+1 行,每行有 P 个正整数,其中第 i 行(从 00 开始计数)的第 j 个(从 0 开始计数)正整数表示点 (j,i) 到点 (j+1,i) 的路径上生物标本的价值。
接下来的 a 行,每行有 3 个整数 k,x,y,表示有 k 个深海机器人从 (x,y) 位置坐标出发。
再接下来的 b 行,每行有 33 个整数 r,x,y,表示有 r 个深海机器人可选择 (x,y) 位置坐标作为目的地。
输出格式
输出采集到的生物标本的最高总价值。
数据范围
1≤a≤4,
1≤b≤6,
1≤P,Q≤15,
1≤k,r≤10,
0≤x≤P
0≤y≤Q,
各个生物标本价值不超过 200。
输入样例:
1 1
2 2
1 2
3 4
5 6
7 2
8 10
9 3
2 0 0
2 2 2
输出样例:
42解析:
本题做法可参考:382. K取方格数(图论,费用流,拆点,上下界可行流,网格图模型)-CSDN博客
#include<iostream>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<map>
#include<sstream>
#include<deque>
#include<unordered_map>
#include<unordered_set>
#include<bitset>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef pair<int, int> PII;
const int N = 16*16+10, M = (N * 4) * 2 + 10, INF = 0x3f3f3f3f;
int n,m,P, Q, S, T;
int h[N], e[M], f[M], w[M], ne[M], idx;
int q[N], d[N], pre[N], incf[N];
bool st[N];int get(int a, int b) {return a * (Q + 1) + b;
}void add(int a, int b, int c,int d) {e[idx] = b, f[idx] = c, w[idx] = d, ne[idx] = h[a], h[a] = idx++;e[idx] = a, f[idx] = 0, w[idx] = -d, ne[idx] = h[b], h[b] = idx++;
}bool spfa() {int hh = 0, tt = 1;memset(d, -0x3f, sizeof d);memset(incf, 0, sizeof incf);q[0] = S, d[S] = 0, incf[S] = INF;while (hh != tt) {int t = q[hh++];if (hh == N)hh = 0;st[t] = 0;for (int i = h[t]; i != -1; i = ne[i]) {int j = e[i];if (d[j] < d[t] + w[i] && f[i]) {d[j] = d[t] + w[i];incf[j] = min(incf[t], f[i]);pre[j] = i;if (!st[j]) {st[j] = 1;q[tt++] = j;if (tt == N)tt = 0;}}}}return incf[T] > 0;
}int EK() {int cost = 0;while (spfa()) {int t = incf[T];cost += t*d[T];for (int i = T; i != S; i = e[pre[i]^1]) {f[pre[i]] -= t;f[pre[i] ^ 1] += t;}}return cost;
}int main() {cin >> n >> m >> P >> Q;memset(h, -1, sizeof h);S = (P + 1) * (Q+1), T = S + 1;for (int i = 0,a; i <= P; i++) {for (int j = 0; j < Q; j++) {scanf("%d", &a);add(get(i, j), get(i, j + 1), 1, a);add(get(i, j), get(i, j + 1), INF, 0);}}for (int i = 0,a; i <= Q; i++) {for (int j = 0; j < P; j++) {scanf("%d", &a);add(get(j, i), get(j + 1, i), 1, a);add(get(j, i), get(j + 1, i), INF, 0);}}for (int i = 1,k,x,y; i <= n; i++) {scanf("%d%d%d", &k, &x, &y);add(S, get(x, y), k, 0);}for (int i = 1, r, x, y; i <= m; i++) {scanf("%d%d%d", &r, &x, &y);add(get(x,y),T, r, 0);}printf("%d\n", EK());return 0;
}








)










