惯性导航 | 测量方程中的噪声模型与离散时间噪声模型
- IMU测量方程中的噪声模型
- IMU的离散时间噪声模型
IMU测量方程中的噪声模型
在大多数系统中,IMU的噪声由两部分组成:测量噪声(Measurement Nosie)与零偏(Bias)。
原因:
由于各种各样的原因,即使在车辆静止时,IMU的角速度和加速度输出也不一定形成均值为0的白噪声,而是带有一定的偏移。
这个偏移量是由IMU内部的机电测量装置导致的,有些IMU的偏移较小,也有的会比较大。
同时该偏移量还受温度等因素的影响,随时间发生变化。
在数学上,我们将它建模出来,认为零偏也是系统的状态量,而且随时间随机改变。但是这是一种数学建模,并非系统本质。
我们并不是从IMU的机械特性或者物理特性得出零偏的变化关系,也没有在物理上描述IMU零偏和温度之间的关系,即使这种关系客观存在。
我们只是假定数学模型是这样的,然后看它与实际的IMU器件读数是否有明显的差异。
记陀螺仪和加速度计的测量噪声分别为 η g \eta _{g} ηg, η a \eta _{a} ηa,同时记零偏为 b g b _{g} bg, b a b _{a} ba,下标g表示陀螺仪,a表示加速度计。那么这几个参数在测量方程中表现为:
a ~ = R T ( a − g ) + b a + η a ω ~ = ω + b g + η g \begin{matrix} \tilde{a} =R^{T} (a-g)+b _{a}+\eta _{a} \\ \tilde{\omega } =\omega +b _{g}+\eta _{g} \end{matrix} a~=RT(a−g)+ba+ηaω~=ω+bg+ηg
在连续时间下,我们认为IMU测量噪声是一个方差为 C o v ( η g ) Cov(\eta _{g}) Cov(ηg), C o v ( η a ) Cov(\eta _{a}) Cov(ηa)的零均值白噪声高斯过程。
认为零偏是一个维纳过程(Wiener Process)或布朗运动或随机游走(Random Walk)。
对于一个均值为零、协方差为 Σ \Sigma Σ的白噪声高斯过程随机变量 w ( t ) w(t) w(t)可以写为
w ( t ) ∼ G P ( 0 , Σ δ ( t − t ′ ) ) w(t)\sim GP(0,\Sigma \delta (t-t^{'} )) w(t)∼GP(0,Σδ(t−t′))
其中, Σ \Sigma Σ称为能量密度矩阵, δ \delta δ为狄拉克函数。狄拉克函数的存在可以轻松的从连续时间的高斯过程推导离散时间采样之后的IMU测量噪声。
一个普通的零偏b的随机游走过程可以建模为:
b ˙ ( t ) = η b ( t ) \dot{b}(t)=\eta _{b} (t) b˙(t)=ηb(t)
其中 η b ( t ) \eta _{b} (t) ηb(t)也是一个高斯过程。于是 b g b _{g} bg和 b a b _{a} ba的随机游走都可以建模为:
b ˙ a ( t ) = η b a ( t ) ∼ G P ( 0 , C o v ( b a ) δ ( t − t ′ ) ) b ˙ g ( t ) = η b g ( t ) ∼ G P ( 0 , C o v ( b g ) δ ( t − t ′ ) ) \begin{matrix} \dot{b}_{a}(t) = \eta _{ba} (t)\sim GP(0,Cov(b_{a})\delta (t-t^{'} )) \\ \dot{b}_{g}(t) = \eta _{bg} (t)\sim GP(0,Cov(b_{g})\delta (t-t^{'} )) \end{matrix} b˙a(t)=ηba(t)∼GP(0,Cov(ba)δ(t−t′))b˙g(t)=ηbg(t)∼GP(0,Cov(bg)δ(t−t′))
随机过程可以从直观上理解,由于高斯过程的协方差随时间变得越来越大,IMU的测量值会随着采样时间变长而变得更加不准确,因此采样频率越高的IMU,其精度也会相对较高。而零偏部分由布朗运动描述,呈现随机游走状态。表现在实际当中,则可以认为一个IMU的零偏会从某个初始值开始,随机的向附近做不规律的运动。运动的幅度越大,就称它的零偏越不稳定。
所以质量好的IMU,零偏应该保持在初始值附件不动。
随机游走实际上就是导数为高斯过程的随机过程。从IMU的角度来看,由于我们关心的是测量的角速度和加速度,所以零偏部分看起来是随机游走。
若从高一级的系统层面来看,角速度就是角度的导数,加速度又是速度的导数,所以IMU的测量噪声,也可以解释为角度的随机游走和速度的随机游走。
IMU的离散时间噪声模型
在连续时间下的IMU噪声方程比较复杂,但在离散时间下简单。
现实中的IMU会按照固定时间间隔对运动物体的惯性进行采样,因此总可以将拿到的数据看成离散的。
IMU传感器按照固定频率进行采样,设每次采样间隔为 △ t \bigtriangleup t △t ,那么对于噪声来说,陀螺仪和加速度计的离散测量噪声可以简化地描述为:
η a ( k ) ∼ N ( 0 , 1 △ t C o v ( η a ) ) η g ( k ) ∼ N ( 0 , 1 △ t C o v ( η g ) ) \begin{matrix} \\ \eta _{a}(k)\sim \mathcal{N} (0,\frac{1}{\triangle t} Cov(\eta _{a})) \\ \eta _{g}(k)\sim \mathcal{N} (0,\frac{1}{\triangle t} Cov(\eta _{g})) \end{matrix} ηa(k)∼N(0,△t1Cov(ηa))ηg(k)∼N(0,△t1Cov(ηg))
对于零偏部分,则可以写为
b g ( k + 1 ) − b g ( k ) ∼ N ( 0 , △ t C o v ( b g ) ) b a ( k + 1 ) − b a ( k ) ∼ N ( 0 , △ t C o v ( b a ) ) \begin{matrix} \\ b_{g}(k+1)-b_{g}(k)\sim \mathcal{N} (0,\triangle t Cov(b _{g})) \\ b_{a}(k+1)-b_{a}(k)\sim \mathcal{N} (0,\triangle t Cov(b _{a})) \end{matrix} bg(k+1)−bg(k)∼N(0,△tCov(bg))ba(k+1)−ba(k)∼N(0,△tCov(ba))
在离散时间系统中,两个噪声都是便于处理的。
在很多系统实现中,甚至不用考虑用协方差矩阵来表示IMU测量噪声和零偏随机游走,而是简单地将它们表示为对角矩阵,这实际上忽略了各个轴之间的相关性。
在程序里,使用 σ g , σ a \sigma _{g},\sigma _{a} σg,σa的参数表示IMU的噪声标准差,用 σ b g , σ b a \sigma _{bg},\sigma _{ba} σbg,σba 参数表示零偏游走的标准差。
离散时间下的噪声标准差应该为:
σ g ( k ) = 1 △ t σ g , σ a ( k ) = 1 △ t σ a σ b g ( k ) = △ t σ b g , σ b a ( k ) = △ t σ b a \begin{matrix} \\ \sigma _{g}(k) = \frac{1}{\sqrt{\triangle t} } \sigma _{g} ,\sigma _{a}(k) = \frac{1}{\sqrt{\triangle t} } \sigma _{a} \\ \sigma _{bg}(k) = \sqrt{\triangle t} \sigma _{bg} ,\sigma _{ba}(k) = \sqrt{\triangle t} \sigma _{ba} \end{matrix} σg(k)=△t1σg,σa(k)=△t1σaσbg(k)=△tσbg,σba(k)=△tσba
在进行惯导的滤波器实现和预积分时,会用到这些符号来配置IMU的噪声情况。
如何得到噪声参数?
IMU产品普遍提供自身的参数手册,以说明它在出厂时的数据精度、稳定性等指标。 这些指标也可以指导我们调节状态估计算法的权重。
算法相关的主要参数有以下几项
- 测量噪声。在整个运动模型看来是角度随机游走和速度随机游走,对应离散时间噪声模型中的 σ g , σ a \sigma _{g},\sigma _{a} σg,σa。也可以简单地称其为陀螺白噪声和加速度计白噪声。
- 零偏随机游走方差。也就是噪声模型中的 σ b g , σ b a \sigma _{bg},\sigma _{ba} σbg,σba 。通常在手册中没有直接的对应项,在实际中也很难测量到。手册中经常用零偏重复性和运动时偏置稳定性来代替它。
刚打开IMU时,可以在静止状态下估计IMU零偏。每次零偏的大小变化由零偏重复性来描述。另外,如果其它客观条件不变,则这个开机零偏在运动过程中也会发生一定改变,其幅值就由运动时零偏稳定性来描述。
在理想条件下,可以认为IMU的零偏会在初始零偏附件的运动时零偏稳定性这个范围内。然而实际中的IMU往往不会运行在恒温条件下,其零偏变化需要实时进行估计。整体而言,可以参考这个指标来设定零偏随机游走的幅值大小。
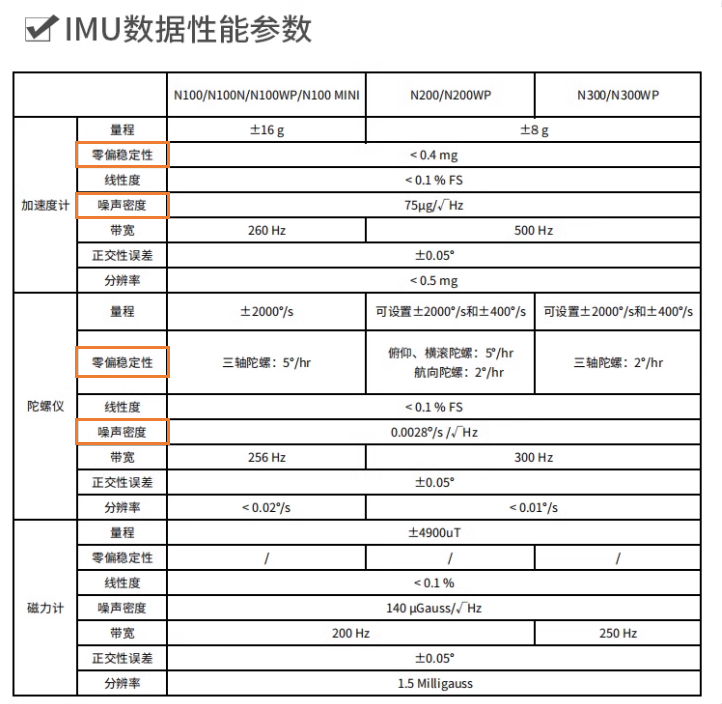
例如网上随便找的可这个IMU

在IMU数据性能参数上面可以查到 测量噪声 、零偏稳定性(运动时零偏稳定性)的参数 。没有提供零偏重复性参数。

数据包)


 笔记-2)






)

是如何赋能数字化市场营销全过程?- 我为什么要翻译介绍美国人工智能科技巨头IAB公司)





