冯·诺依曼计算机

计算机结构

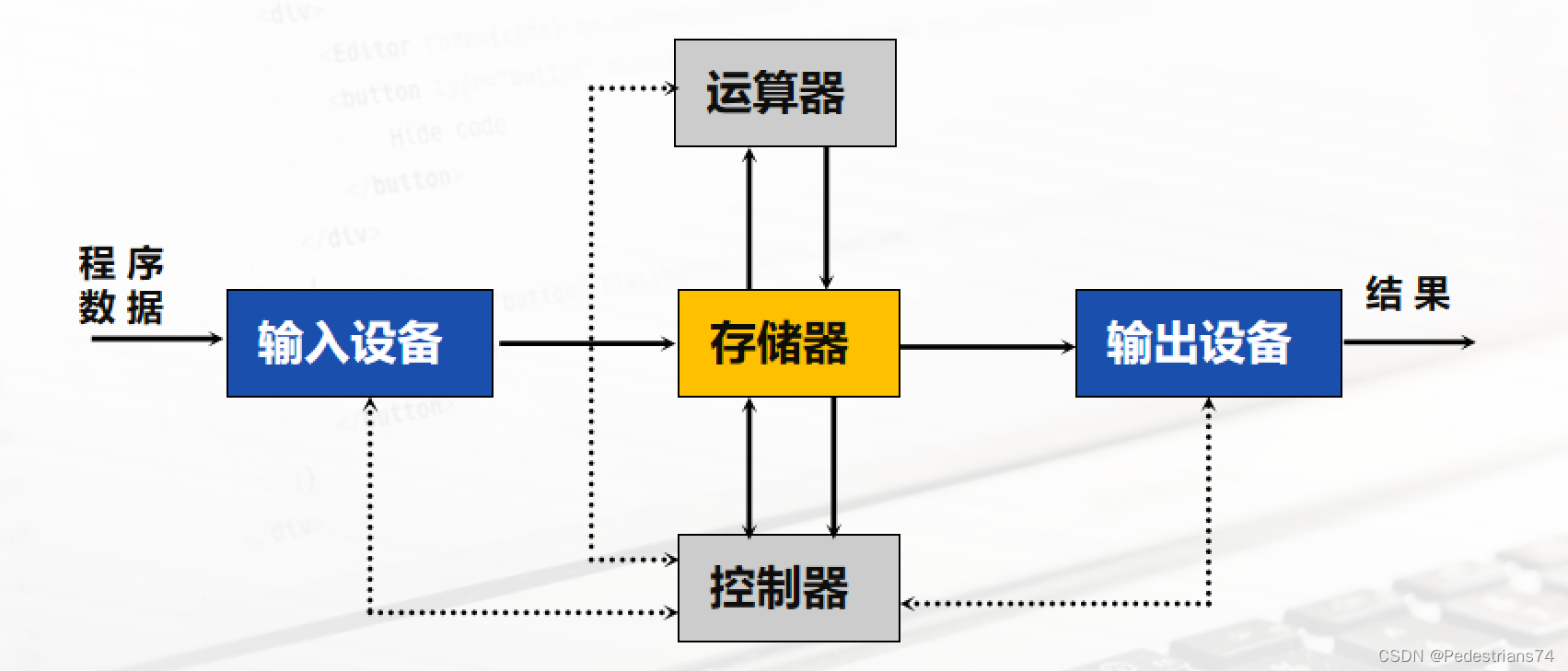
计算机特点

1.采用二进制

2.程序存储

2.由五大部件组成计算机系统：运算器、存储器、控制器、输入设备和输出设备

计算机硬件系统的层次

中央处理器（CPU）：运算器 + 控制器

计算机主机：CPU+存储器

计算机系统：主机+输入设备 + 输出设备

运算器主要部件

算术逻辑单元（ALU）：完成算术运算、逻辑运算

通用寄存器（GR）：暂存运算数据和运算结果

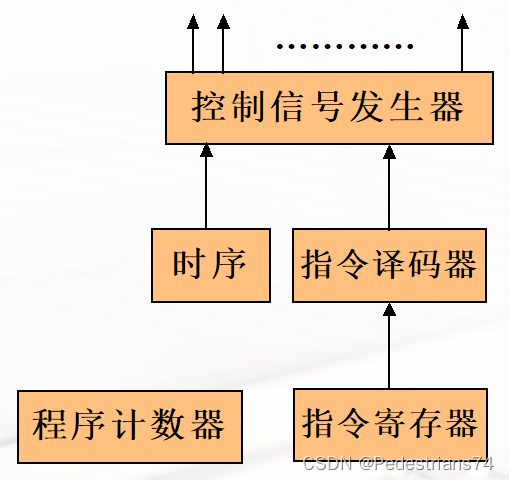
控制器的组成

PC（程序计数器）：存放指令的地址

IR（指令寄存器）：存放当前正在执行的指令

ID（指令译码器）：分析指令

时序部件

控制信号发生器

存储器

存储器的读写（访问）

按地址访问，一次只能读或写一个单元

向存储器里存入信息称为写入，写入的新内容覆盖了原来的旧内容；（一挤就走）

从存储器里取出信息称为读出，信息读出后并不破坏原来存储的内容。（取之不尽）

尚未写入之前的初始值通常是不确定的，上电后任何时刻存储单元都是有内容的

总线

能为系统中多个部件分时、共享的一组信息传输线及相关逻辑

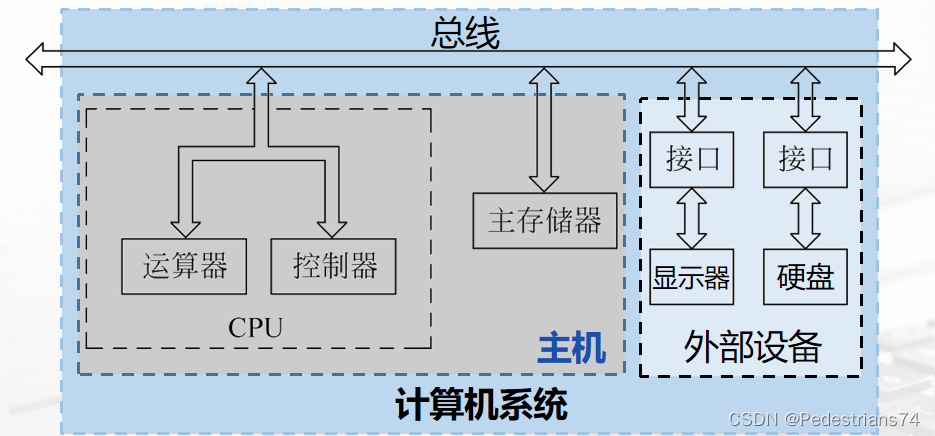
计算机系统

如下图所示

主要性能指标

执行时间是唯一准确的指标！

主频

CPU时钟的频率，单位：Hz

时钟周期 = 1/时钟频率

CPI

执行每条指令所需的平均时钟周期数

平均指令周期

指令周期是指完成一条指令的时间

不同指令的指令周期不尽相同，可以用平均指令周期反映计算机指令的执行速度

MIPS

单位时间内执行指令的平均条数（以百万为单位）

FLOPS

每秒执行多少次浮点运算

表示数量级的前缀：MFLOPS……

进制表示

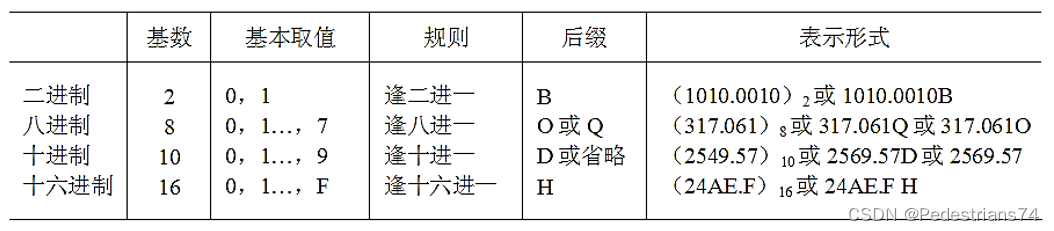
进制转换

十进制转二进制：整数部分除二取余倒排列，小数部分乘二取整正排列（其余以此类推）

定点数表示

无符号定点数

无符号数是指整个机器字长的全部二进制位均表示数值位，计算机中的无符号数通常指的是无符号定点整数

n位无符号定点整数可表示的最小值为0，编码为00…0，可表示的最大值为2的n次幂－1，编码为11…1

有符号定点数

真值：用+、－符号加绝对值来表示的实际数值

机器数：正负符号数字化放在有效数字的前面

定点小数：小数点约定在数符和最高数值位之间

定点整数：小数点约定在最低数值位的右边

数值表示

1.原码

原码由符号位和数值位组成，最高位表符号，后面是数值位

若X为正数，则使符号位为“0”，数值部分与X的数值位相同

若X为负数，则使符号位为“1”，数值部分与X的数值位相同

在原码表示中，0有两种不同形式，即[＋0]原=0.00…0, [－0]原=1.00…0

2.反码

正数反码同原码

负数反码，符号位不变，数值位取反

在补码表示中，0有两种不同形式，即[＋0]反=0.00…0, [－0]反=1.11…1

3.补码

补码由符号位和数值位组成，最高位表符号，后面是数值位；

若X为正数，则使符号位为“0”，数值部分与X的数值位相同

若X为负数，则使符号位为“1”，数值部分为X的数值位各位取反，然后加1

在补码表示中，0只有一种形式，即[＋0]补=[－0]补=0.00…0

相反数的补码：[-X]补为[X]补连同符号位在内一起求反加一，这个过程称为求补。

4.移码

定点整数（X为n-1位真值，移码位数为n ）

定点小数（X为真值，小数的有效数值位为n-1位，移码位数为n ）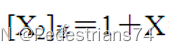

同一个真值的移码和补码仅差一个符号位，若将补码的符号位取反，即可得到真值的移码

在移码表示中，0的表示式是唯一的，即［+0］移=100…0,［-0］移=100…0

8位无符号数、原码、补码、反码和移码所对应的真值

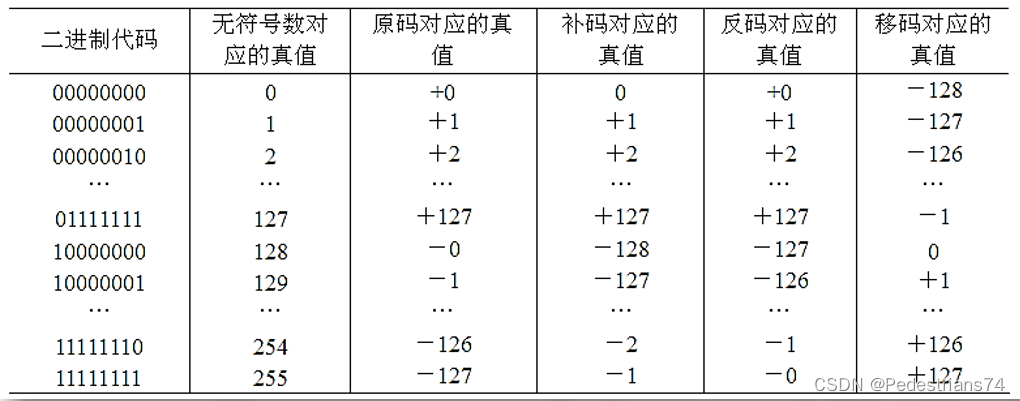
浮点数表示

N=M×R的E次幂＝±m ×R的±e 次幂

E为浮点数的阶码，一般为定点整数，常用补码或移码表示；

M为浮点数的尾数，一般为定点小数，常用补码或原码表示；

R为浮点数的基数，基数在浮点数的表示中是隐含的。

一般表示格式：

浮点数的数据范围：

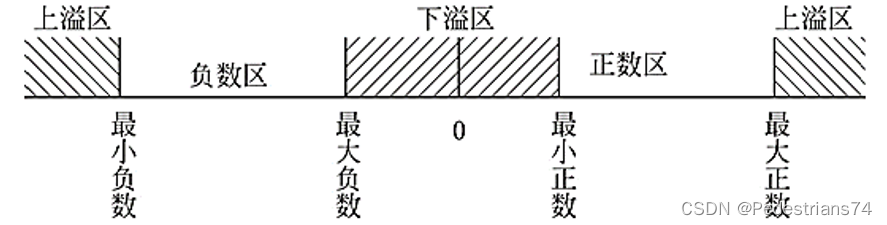
例题如下

非数值数据的表示

国际上广泛采用的是美国国家信息交换标准代码，简称 ASCII 码

Unicode编码：为每种语言中的每个字符设定了统一并且唯一的二进制编码，以满足跨语言、跨平台进行文本转换、处理的要求，但会使文件的容量变大

UTF-8编码：用可变数目的字节对字符进行编码，字节的个数可以是1到4个

汉字字形码：用0、1表示汉字的字形，将汉字放入n行×ｎ列的正方形内，该正方形共有n²个小方格，每个小方格用一位二进制表示，凡是笔画经过的方格值为1，未经过的值为0，如下图所示：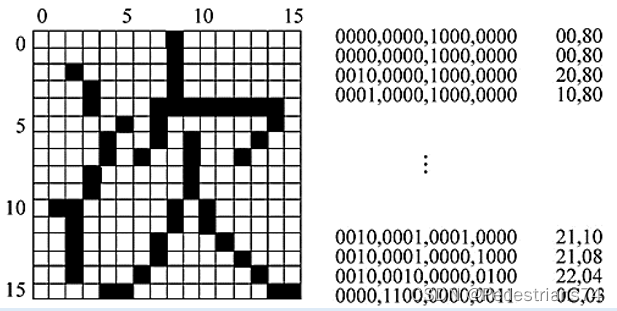

奇偶校验码：由信息位和校验位两部分组成，校验位是附加的冗余位，只有一位

        奇校验：校验位的取值0或1使得整个代码中 “1”的个数为奇数

        偶校验：校验位的取值0或1使得整个代码中 “1”的个数为偶数