题目
文件组合
待传输文件被切分成多个部分,按照原排列顺序,每部分文件编号均为一个 正整数(至少含有两个文件)。传输要求为:连续文件编号总和为接收方指定数字 target 的所有文件。请返回所有符合该要求的文件传输组合列表。
注意,返回时需遵循以下规则:
每种组合按照文件编号 升序 排列; 不同组合按照第一个文件编号 升序 排列。
示例 1:
输入:target = 12 输出:[[3, 4, 5]] 解释:在上述示例中,存在一个连续正整数序列的和为 12,为 [3, 4, 5]。
示例 2:输入:target = 18 输出:[[3,4,5,6],[5,6,7]] 解释:在上述示例中,存在两个连续正整数序列的和分别为18,分别为 [3, 4, 5, 6] 和 [5, 6, 7]。
提示:
1 <= target <= 10^5
解法1:分类
- 这种做法是笔者最朴素的想法:如果遍历小于 target 的每一个数,逐个相加尝试该数是否能组成一个符合条件的文件序列,那时间复杂度太高了(其实这种就是滑动窗口的思想,复杂度只有O(N))。于是我想能否在遍历到这个数的同时,直接根据这个数与 target 之间的某种关系判断其能否形成合适的序列,于是在观察到文件序列其实是等差数列后,我决定依据等差数列的特点对其进行分类
- 使用 i 进行遍历。文件序列如果有奇数个元素,则可以找到等差中项,target 能整除 i 且 n = target / i 必须为奇数
- 文件序列如果有偶数个元素,则target 能整除 i + i+1 且 n 和 target 的奇偶必须相同(!((n+target)%2))(因为n 表示有n对i + i+1,而i + i+1必为奇数,所以当n为偶数的时候,n对i + i+1的和为偶数;n为奇数的时候,n对i + i+1的和为奇数。所以 n 和 target 的奇偶必须相同)
- 由于题目要求不同组合按照第一个文件编号 升序 排列,而当我遍历 i 时,无法确定由 i 作为靠中间的元素的这个序列的头部是多少,所以我使用了 map 存储,利用了 map 会自动排序 key 的特点(结构:map<第一个文件编号,文件编号序列的 vector>)
class Solution {
public:vector<vector<int>> fileCombination(int target) {vector<vector<int>> all;map<int, vector<int>> forOrder;for(int i=1; i<=(target+1)/2; ++i){if(!(target%i)){//target 能整除 i,则可能的组合有奇数个元素int n = target / i;if(n%2 && i>n/2){//n 为组合中元素的个数,必须为奇数vector<int> group;for(int j=i-n/2; j<=i+n/2; ++j){group.push_back(j);}forOrder[i-n/2] = group;}}if(!(target%(i + i+1))){//target 能整除 i + i+1,可能的组合必为偶数个元素int n = target/(i + i+1);if(!((n+target)%2) && i-(n-1)>0){//n 和 target 的奇偶必须相同vector<int> group;for(int j=i-(n-1); j<=(i+1)+(n-1); ++j){group.push_back(j);}forOrder[i-(n-1)] = group;}}}// 将 forOrder 中的元素按顺序存入 all 中for (const auto& pair : forOrder) {all.push_back(pair.second);}return all;}
};
解法2:滑动窗口(双指针)
- 这种想法也很简单,从 i=1 开始,计算其后连续的序列的和,如果和小于 target,那么就在和的基础上往后再加一个数字;如果和大于 target 了,则表明此时的 i 作为开始元素找不到合适的序列,此时 i 往后移动,并记得让和减去上一个 i
- 这种想法虽然是遍历求和,并比较和与目标值,但是时间复杂度并不高,这是因为每次遍历和的计算都是在上一轮和的计算结果上进行的
- 由于是从 i=1 开始遍历,逐渐求和比较,故不存在有的序列会遍历不到的问题
//滑动窗口vector<vector<int>> fileCombination(int target) {vector<vector<int>> all;int i=1, j=2, sum=i+j;while(i<j){if(sum == target){vector<int> group;for(int k=i; k<=j; ++k){group.push_back(k);}all.push_back(group);}if(sum < target){++j;sum += j;// cout<<"j:"<<j<<"sum"<<sum<<endl;} else{sum -= i;++i;}}return all;}
解法3:等比数列求和公式求解
- 知道序列和 target,知道首项 i,那么可以利用等差数列求和公式 + 二次方程求根公式求出末项 j,遍历 i 找到所有符合的末项 j 即可。由于是使用公式计算,时间复杂度并不高
- 当 j 为整数时,符合条件,此处的判断方法为:if(j == (int)j)
- c++ 中,有int i,当 ii 结果超过int时,需要写成(long)ii,表达式 ii 的结果会首先根据表达式中操作数的类型来决定。如果 i 是整型(int),那么表达式 ii 也会被视为整型运算。
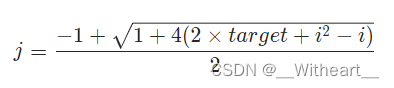
//等差求和公式做法vector<vector<int>> fileCombination(int target) {vector<vector<int>> all;for(int i=1; i<(target+1)/2; ++i){double j = (-1+sqrt(1+4*(2*target+(long)i*i-i)))/2.0;if(j == (int)j){vector<int> group;for(int k=i; k<=(int)j; ++k){group.push_back(k);}all.push_back(group);}}return all;}


)







)

、联合体、枚举)





)
