单调队列其实就是一个队列，只是使用了一点巧妙的方法使得队列中的元素全都是单调递增（或单调递减）的

单挑队列主要解决以下问题：

滑动窗口在滑动时，r++代表右侧数字进入串口，l++代表左侧数字出窗口

这个过程中，想随时得到当前滑动窗口的最大值或最小值

 滑动窗口最大值

具体操作

首先我们先讨论滑动窗口加入数字后，单调队列的情况（也就是r ++ ）

假设这个数组为[6,5,4,3,5,6]

注意我们这个单调队列里只放数组元素的下标，并且里面的下标对应的数值大小是从大到小的

因此我们先放入下标0（也就是a[0]），然后再放入下标1，再放入下标2，再放入下标3

此时碰到了下标4（也就是a[4] = 5）

因为我们是必须严格按照从大到小

所以弹出下标1,2,3

再放入下标4

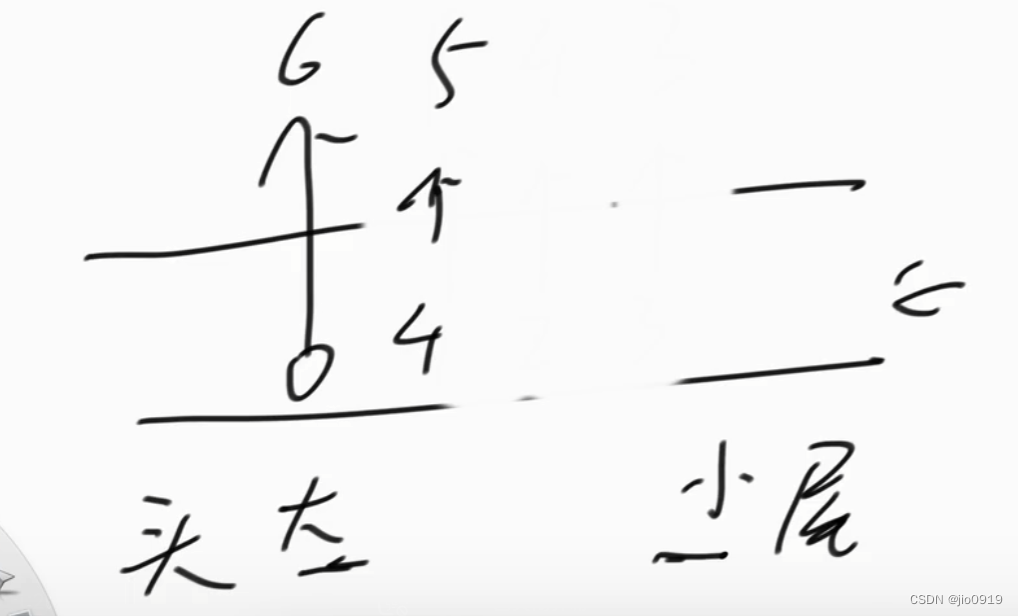
然后碰到了下标5（也就是a[5] = 6）

弹出下标4,0

放入下标5

那滑动窗口中减少数字后，单调队列的操作又该怎么办呢？

我们假设数组为[6,5,4,3,5,6]

假设此时单调队列为

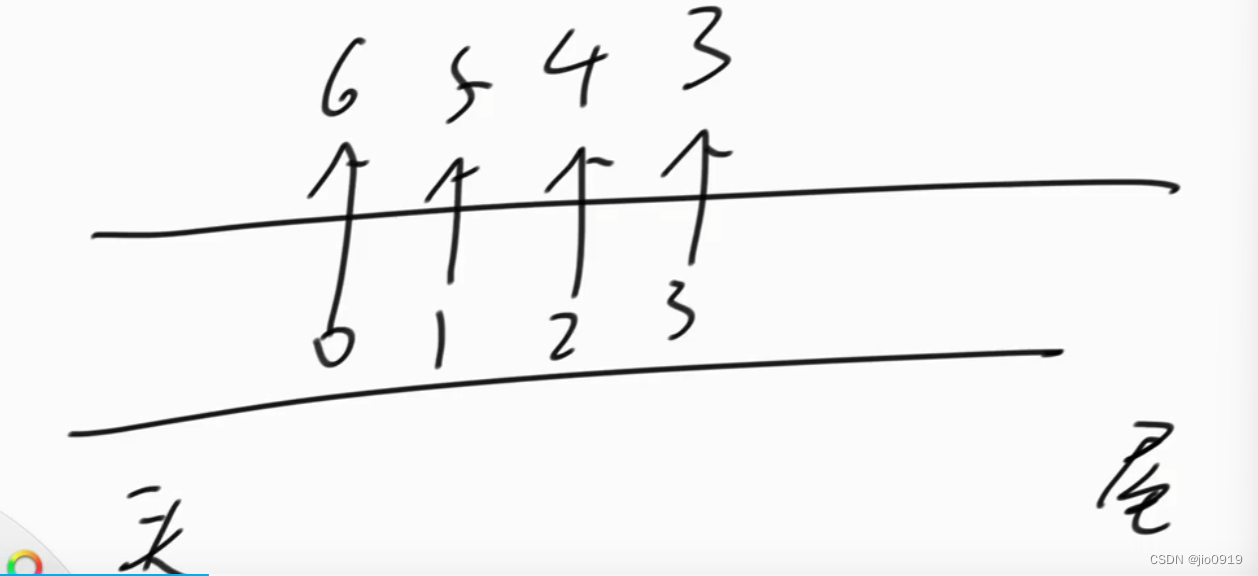
当窗口减少数字（也就是 l ++）

我们就要判断单调队列的头元素是否为过期下标(就是头元素小于 l )

如果是过期下标就把它从头部弹出

解释：

关键点：维持可能性

假设一个队列

我们先放入下标0( a[0] )

如果此时就要求滑动窗口的最大值，那它就是单调队列的头元素

然后我们再放入下标1( a[1] )

为什么要放在下标 0 ( a[0] )的右边?

因此此时滑动窗口的最大值仍然是下标0( a[0] )

但是如果此时让下标 0 ( a[0] )弹出的话（也就是 l ++），此时下标 1 ( a[1] )就是头元素（也就是最大值）

然后我们再放入下标2( a[2] )，它自然也就是放在了下标 1 ( a[1] )的右边（它也有可能会成为最大值）

注意：我们单调队列的存储的都是下标

此时要放入下标4( a[4] )

那我们为什么要弹出1,2,3？

因为它们再也没有机会变成最大值了（因为4位置一定会比1,2,3位置要晚过期，并且4位置的值比1,2,3位置都要大）

 那为什么不弹出6？

因此此时滑动窗口的最大值是下标0( a[0] )。

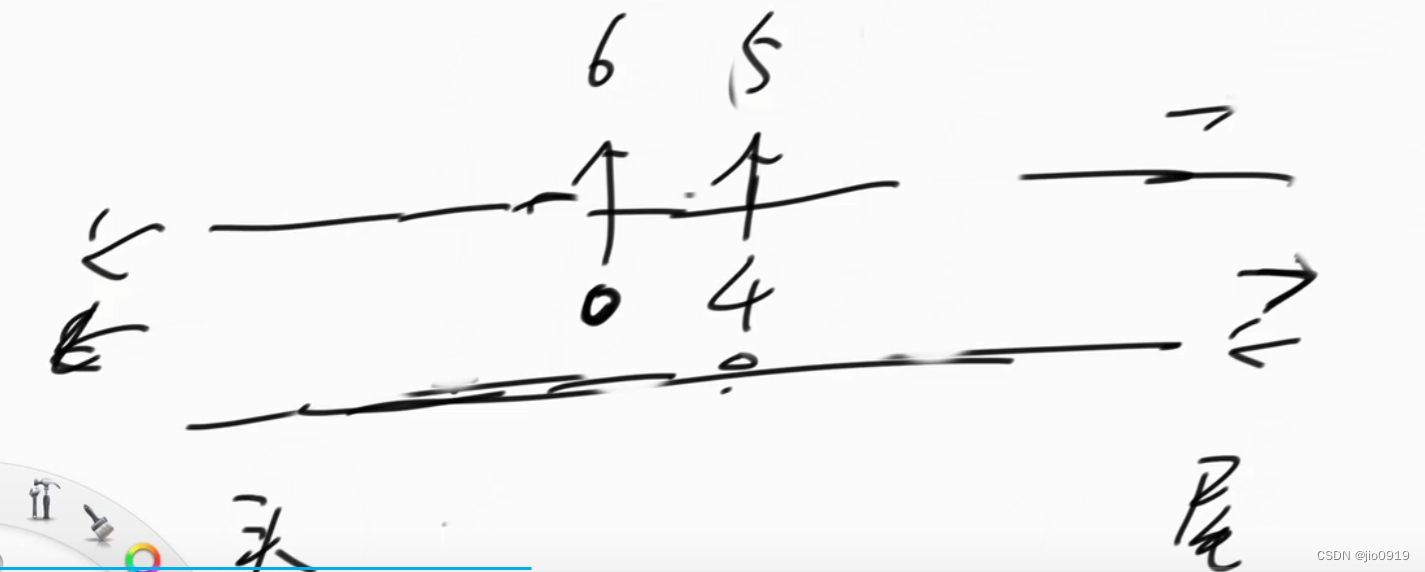
当 l ++时

把 0 从头部弹出

整体的复杂度为o(n)

解题思路：

1.我们先生成 k - 1 的窗口，把它放入单调队列中

2.放入一个元素（r++），放入单调队列中（此时窗口长度为k）

3. l ++ ，考虑单调队列中是否有过期下标（此时窗口长度为k-1）

不断重复2，3

代码：

# include <stdio.h>int main()
{int k;// 滑动窗口大小 int n; //数组长度 scanf("%d %d", &k, &n)int num[n];for (int i=0; i<n; ++i)scanf("%d", &num[i]);int deque[n] //单调队列int h,t; // 用于更新单调队列 h表示头元素的下标，t表示下一个元素该放的位置//当h == t 时表示单调队列里没有元素h = 0;t = 0;	 //先形成k-1的窗口 for (int i=0; i<k-1; ++i){while (h<t && num[deque[t-1]] <= num[i])t = t - 1; //直接将deque的元素进行覆盖 deque[t] = i;t++;}int m = n - k + 1; //进行的次数//当前窗口为k-1长度for (int l=0, r=k-1; l<m; ++l, ++r){//少一个，要让r位置进去while (h<t && num[deque[t-1] <= num[r]])t = t - 1;deque[t] = r;t = t + 1;//让l位置的数出去if (deque[h] == l)h = h + 1;} 
}

算法讲解054【必备】单调队列-上_哔哩哔哩_bilibilihttps://www.bilibili.com/video/BV11h4y1w7Bu/?vd_source=617dcf7ed08ed9625bdfcadc93c4fac7

拓展

除了单调队列最经典的用法之外，在很多问题里单调队列还可以维持求解答案的可能性

1.单调队列里的所有对象按照规定好的单调性来组织

2.当某个对象从队尾进入单调队列时，会从队头或者队尾依次淘汰单调队列里，对后续求解答案没有帮助的对象

3.每个对象一旦从单调队列弹出，可以结算此时这个对象参与的答案，随后这个对象不再参与后续求解答案的过程

4.其实是先有对题目的分析！进而发现单调性，然后利用单调队列的特征去实现

题目：

（一）

假设arr[1,1,1,6,8,2,9,1,5,4,1]

思路：

当我们遍历到 i 下标时，如果子数组必须以 i 为右边界，那么要往左延伸最短的距离能使累加和大于等于k

我们求出一部分的前缀和为

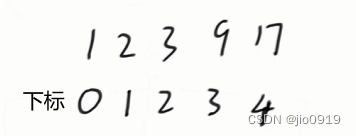
我们必须要找到某一段的前缀和大于等于k，然后再以它右边界的数字为结尾的情况下，向左延伸最短的距离能使累加和大于等于k

例如：

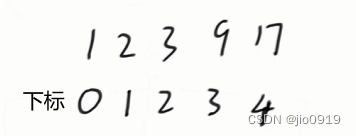
当k = 10时

0~4，它们的前缀和是17，所以我们要找到前面的某段的前缀和小于等于7，且足够靠右，把这段删去，这样就能得到某一段的前缀和大于等于k，并且向左延伸最短的距离能使累加和大于等于k。

0~2的前缀和是3，并且是足够靠右的，所以删去后，得到3~4的前缀和为14，长度为2，满足条件

因此我们可以得到统一的规律：

我们首先要找到以 i 为结尾的前缀和为 x ，并且 x >= k，

要想找到一段的前缀和大于等于k，并且长度最短

必须要删去一段前缀和小于等于 x - k，并且足够靠右的

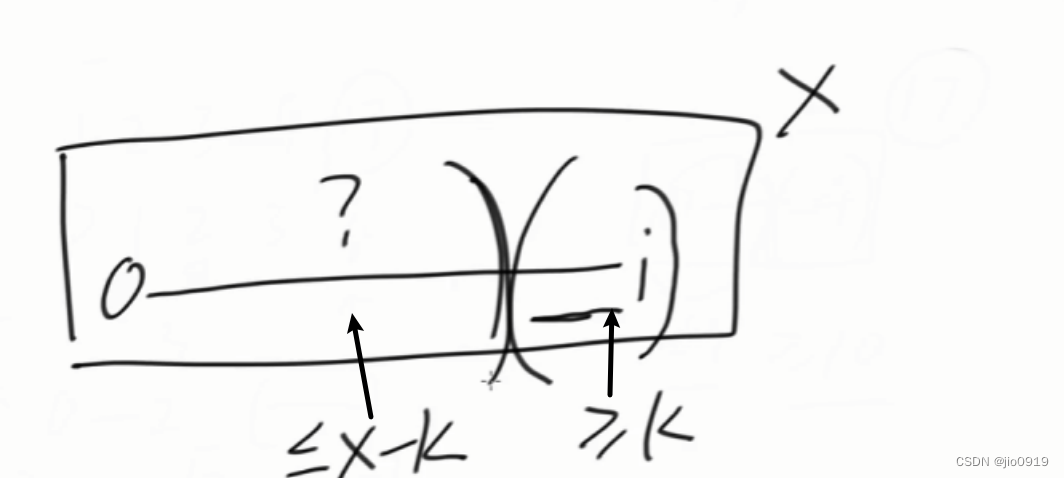
我们建立一个单调队列

存储的是前缀和的下标，下标对应的数值大小是从小到大的

假设arr[1,1,1,6,8,2,9,1,5,4,1]

前缀和为：

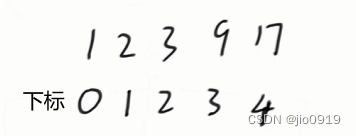
k 为 10

下一个为就是4位置，此时0~4的前缀和为17，大于10，开始判断所有的可能

先判断队头

0~0的前缀和为1，那么1~4的和就是16，符合条件，所以ans = 4

然后把 0 从头部弹出（没有这种0~0的可能性了，因为我们判断出来1~4是符合条件的，我们要求最短的达标子数组，后面的数组肯定会从 1~4 开始往后计算，不会从0开始。换句话说，即使后面的子数组用上了0~0，那它的长度肯定不如是 1~4 短）

继续进行判断队头

0~1的前缀和为2，那么2~4的和就是15，符合条件，所以ans = 3

然后把1从头部弹出

继续进行判断队头

0~2的前缀和为3，那么3~4的和就是14，符合条件，所以ans = 2

然后把2从头部弹出

继续进行判断队头

0~3的前缀和为7，那么4~4的和就是8，不符合条件

然后把 4 从队尾放入单调队列

然后不断进行判断……

综上：

在单调队列中，不断放入前缀和的下标，如果遇到下标对应的前缀和大于等于k，则进行判断

如果我们遇到了负数呢：

看以下的情况：

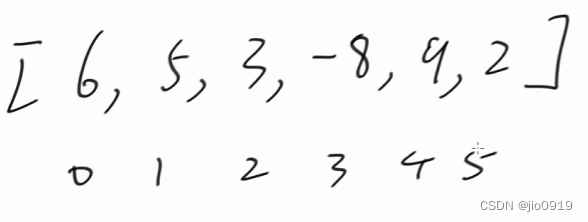
以上为原数组

假设k = 100

此时我们依次放入前缀和的下标

下一个该放入的前缀和下标为3（0~3的前缀和是6）

那么我们就要把0,1,2全部从队尾弹出

（这里就解释了为什么要从小到大进行排列，和为什么要进行弹出操作：1.如果再继续进行下去，如碰到了一个前缀和为 x ，此时x >= k，如果此时x - 6都不符合条件（也就是x - 6 < k），那么x - 14一定是不符合条件的，所以必须要从小到大进行排列。2.因为后加入的数字，与对应的符合条件的 i 点距离肯定是更近的，所以可以把大于等于它的数字都弹出。）

然后和上面相同，不断的进行判断

代码：

# include <stdio.h>int main()
{int kint a[11];scanf("%d", &k);for (int i=1; i<=10; ++i)scanf("%d", &a[i]);int deque[10];int h, t = 0;int md[11];md[0] = 0;md[1] = a[1];for (int i=2; i<=10; ++i)md[i] = md[i-1] + a[i];int ans = 999;int k = 1;for (int i=1; i<=10; ++i){while(h !=t && md[i]-md[deque[h] >=k){ans = min(ans, i - deque[h]);h = h + 1;}while (h < t || md[deque[t-1]]> md[i])t = t - 1;deque[t] = i;t = t + 1;}}
}

（二）

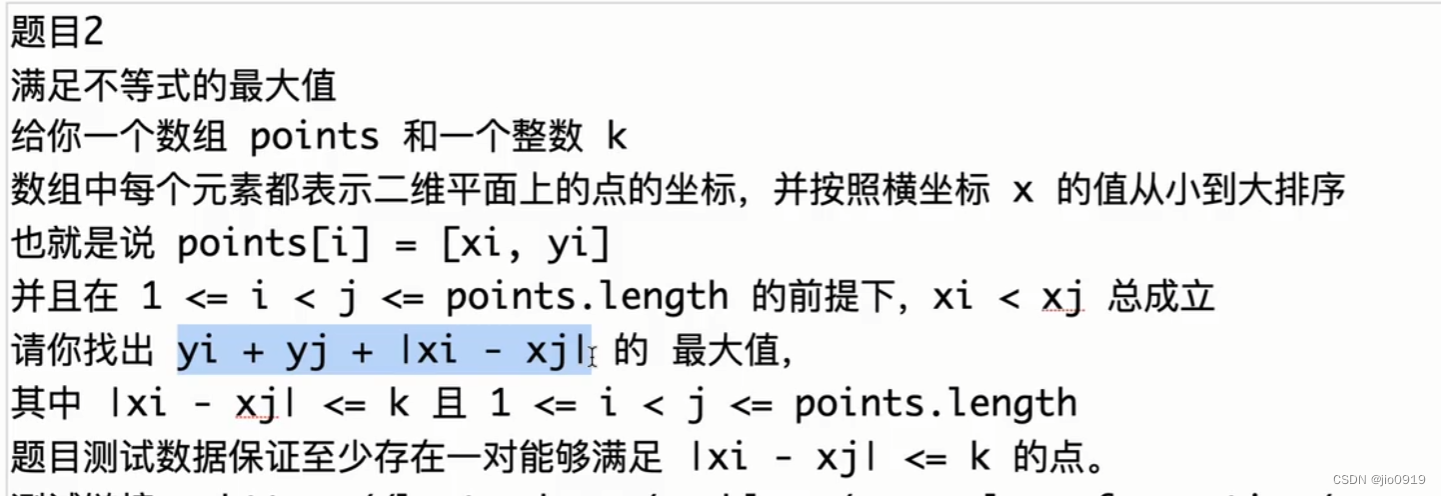
因为 xi 始终大于 xj

所以我们可以直接把绝对值拆掉

所以题目就变为了求 yi + yj + xj - xi = yj + xj + yi - xi；

因此我们可以建立一个滑动窗口的单调队列

里面的元素的是yi - xi的值的下标，从大到小排列

代码：

# include <stdio.h>int main()
{//存储 i号点的 x，y int points[100][2];for (int i=0; i<100; ++i)scanf("%d %d", &points[i][0], &points[i][1]);int deque[100][2];int h, t = 0;int k;int ans = 0;for (int i=0; i<100; ++i){int x = points[i][0];int y = points[i][1];while (h < t && deque[h][0] + k < x)h = h + 1;if (h < t){ans = max(ans, deque[h][1] - deque[h][0] + x + y);}while (h < t && deque[t-1][1] - deque[t-1][0] <= y - x)t = t - 1;}deque[t][0] = x;deque[t][1] = y;t = t + 1;}