概述

1924 年，美国的休哈特博士应用统计数学理论将 3Sigma 原理运用于生产过程中，并发表了

著名的“控制图法”，对产品特性和过程变量进行控制，开启了统计过程控制新时代。

什么是控制图

控制图指示过程何时不受控制，有助于标识是否存在特殊原因变异。如果存在特殊原因变异，则说明过程不稳定且有必要采取纠正措施。

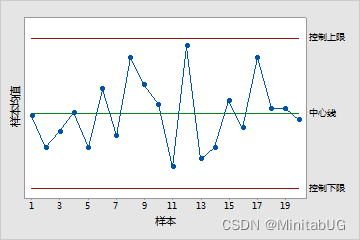
控制图是按时间排序顺序绘制过程数据的图。大多数控制图都包括一条中心线、一个控制上

限和一个控制下限。中心线表示过程均值。控制限表示过程变异。默认情况下，控制限绘制

在中心线上下 3σ 的位置。

随机位于控制限内的点指示过程受控制且仅显示常见原因变异。位于控制限外部或者显示非

随机模式的点指示过程不受控制且存在特殊原因变异。

如何选择合适的控制图

随着控制图的发展，它的类型也是越来越多，那么这时候对于使用 Minitab 的朋友来说，经

常会纠结如何去选择一个合适的控制图。在 Minitab 21 中，协助菜单可以很好的帮助我们去

选择一个合适的控制图。

I-MR 控制图

今天，我们来绘制一下 I-MR 控制图。

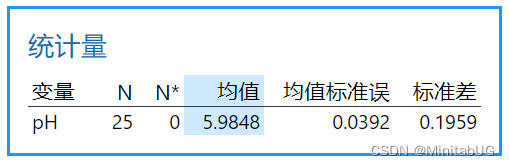
问题背景：某质量工程师监控了液体洗涤剂的生产过程，想要评估该过程是否受控制。这位

工程师测量了 25 个连续批次的洗涤剂的 pH 值。

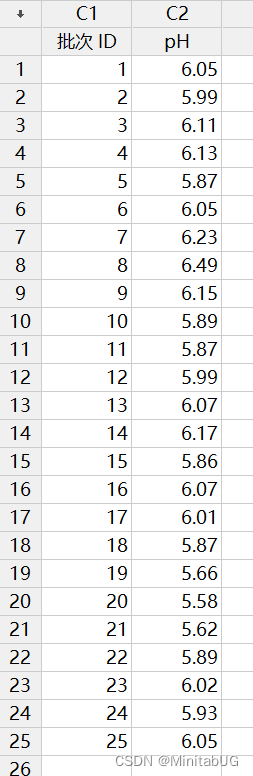
由于 pH 值的数据类型是连续型数据，而且是每批次只取一个样品（子组大小等于 1），故这位工程师创建了一张 I-MR 控制图，以监控洗涤剂的生产过程。

Minitab 绘制 I-MR 控制图

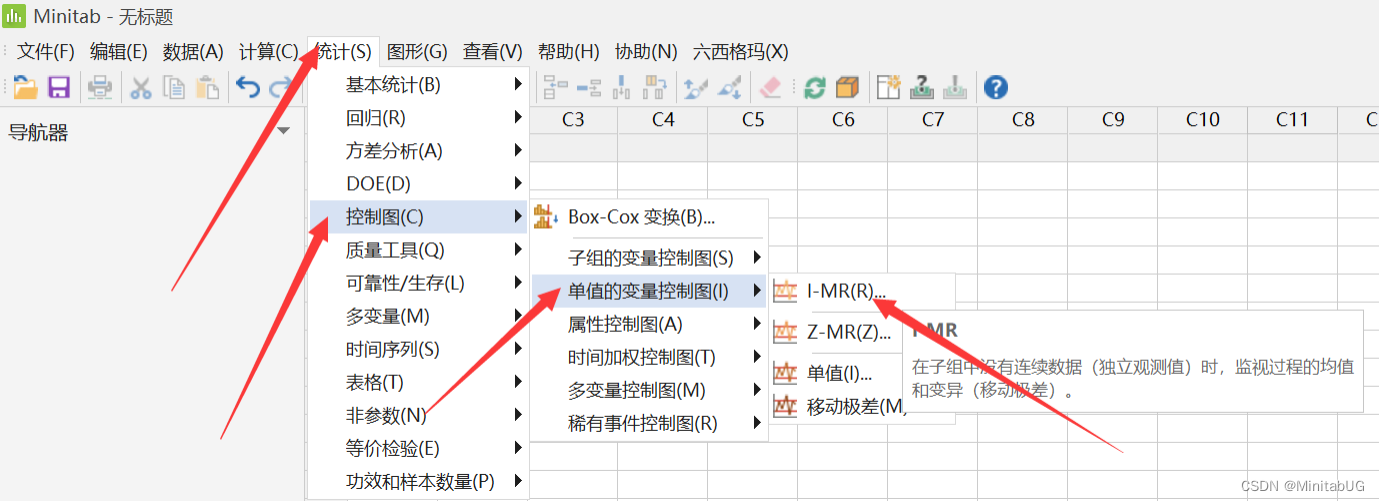
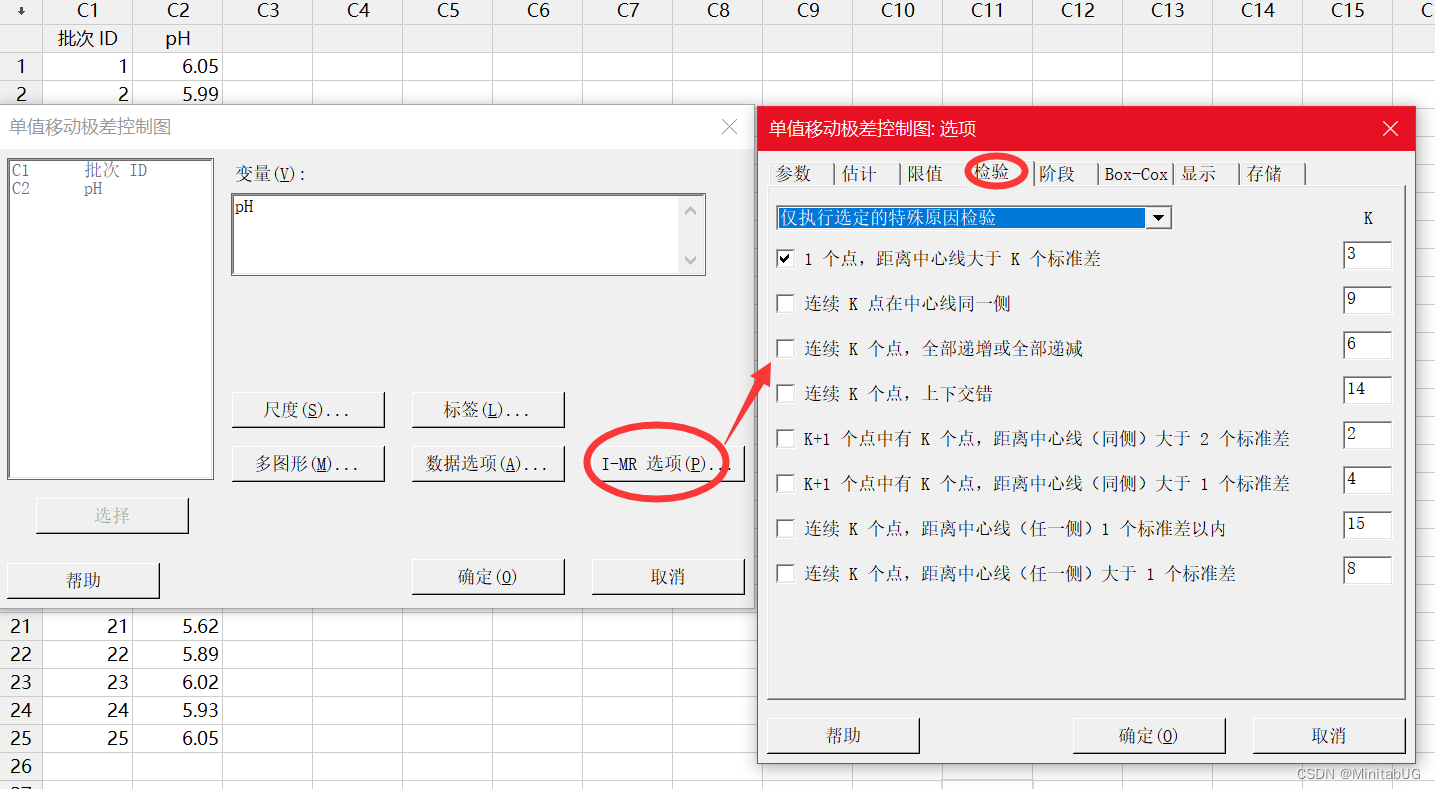
Minitab 结果解释

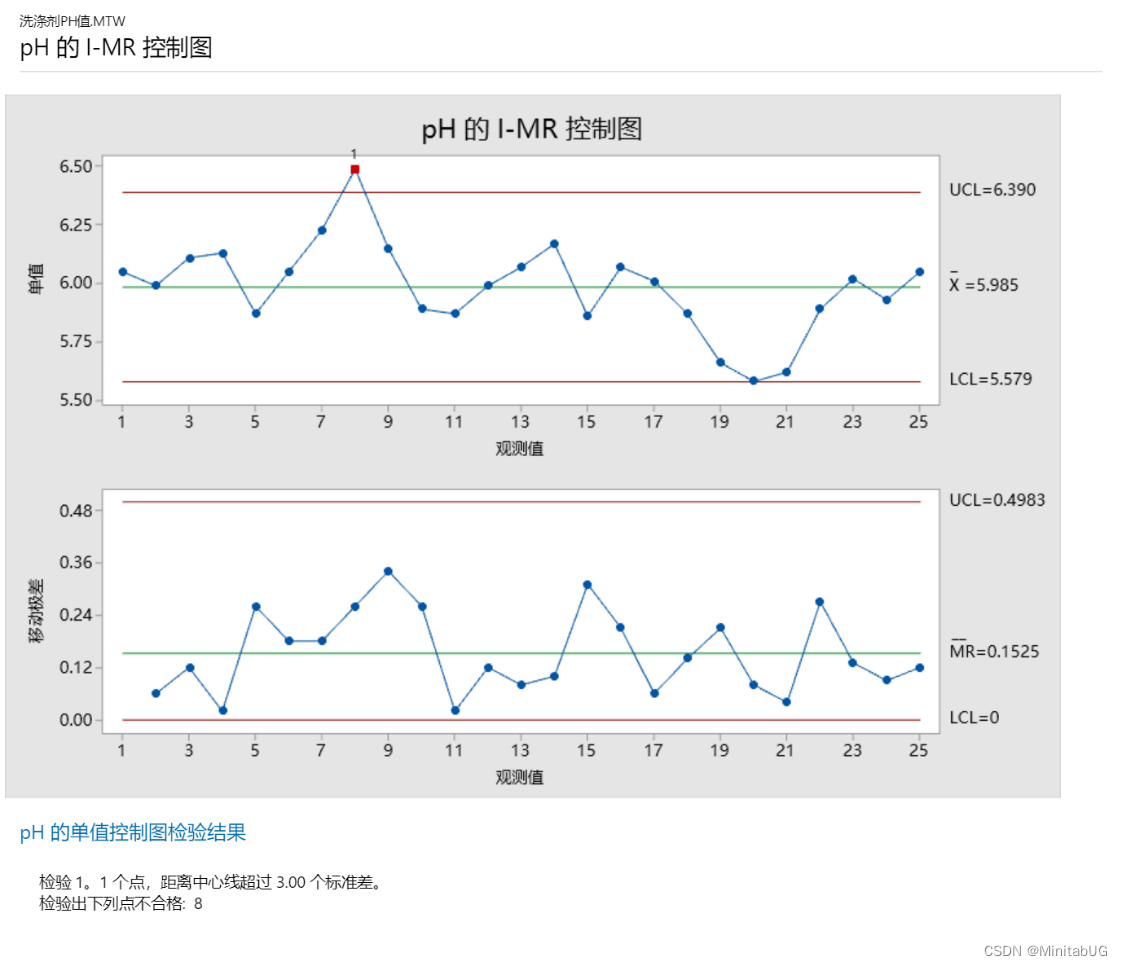
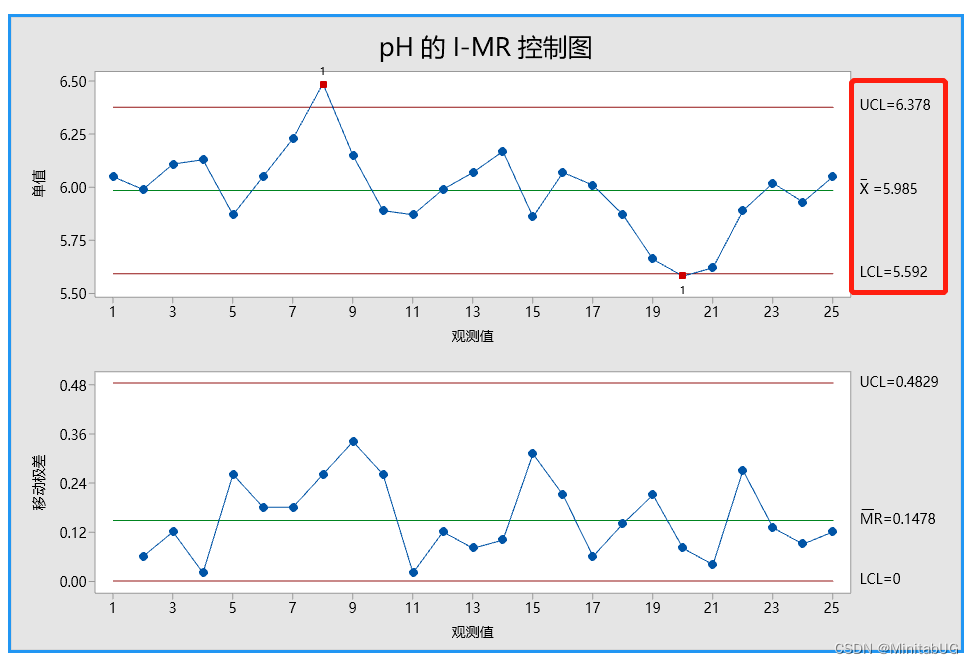
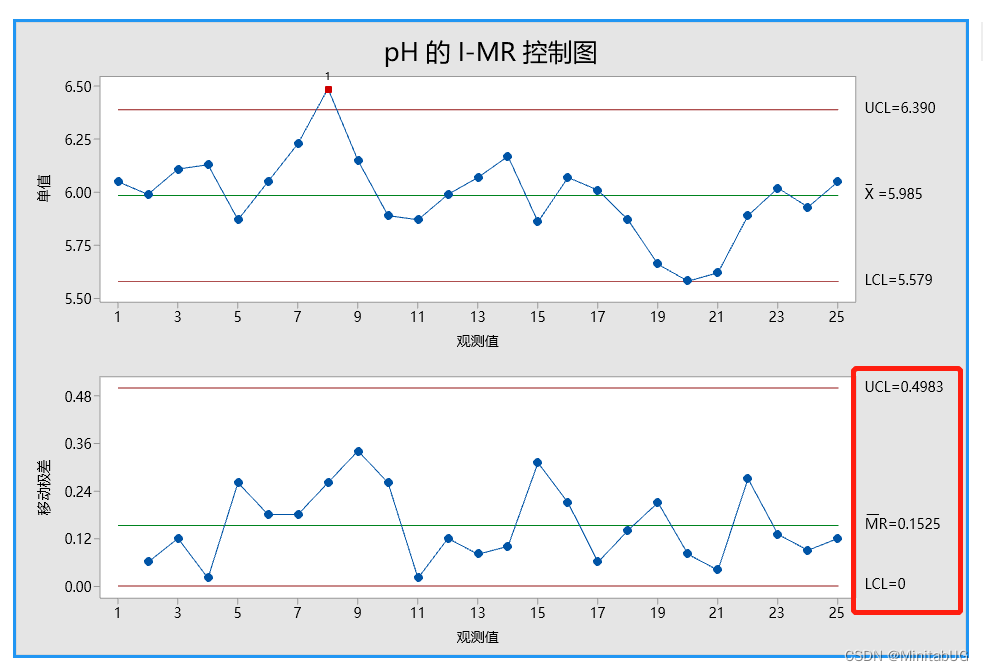
首先解释移动极差控制图（MR 控制图）以检查过程变异。没有位于控制限外部的点且所有

的点都显示出随机模式。因此，过程变异受控制，质量工程师可以检查单值控制图（I 控制

图）上的过程中心。

I 控制图上的一个观测值在检验 1 中失败，因为观测值在中心线上方且距离中心线超过 3

个标准差。

I-MR 控制图的控制限计算（手动）

对于 I-MR 控制图，包含两张图单值控制图（I 控制图）和移动极差控制图（MR 控制图），

我们首先来认识一下这两张图形上的 X 轴、Y 轴、点和线分别表示什么含义。

一、单值控制图（I 控制图）

X 轴：批次 ID

Y 轴：单值（每个批次对应的 pH 值，如单值图上的第二个点表示的是批次 2 的 pH 值）

点：单值控制图（I 控制图）上的每个标绘点是单独的观测值（如上图）。

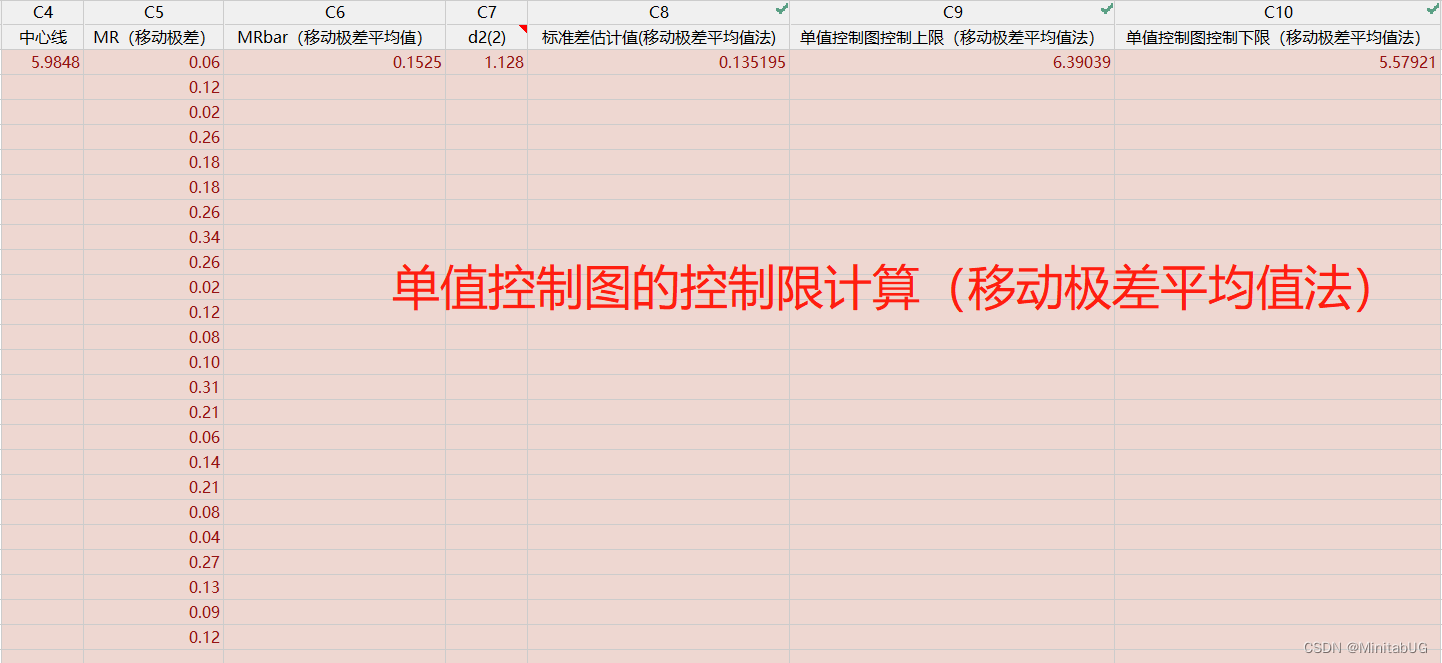
中心线：单值控制图（I 控制图）上的中心线是过程平均值的估计值，计算如下

控制限：单值控制图（I 控制图）控制限的计算结果取决于标准差的估计方式。

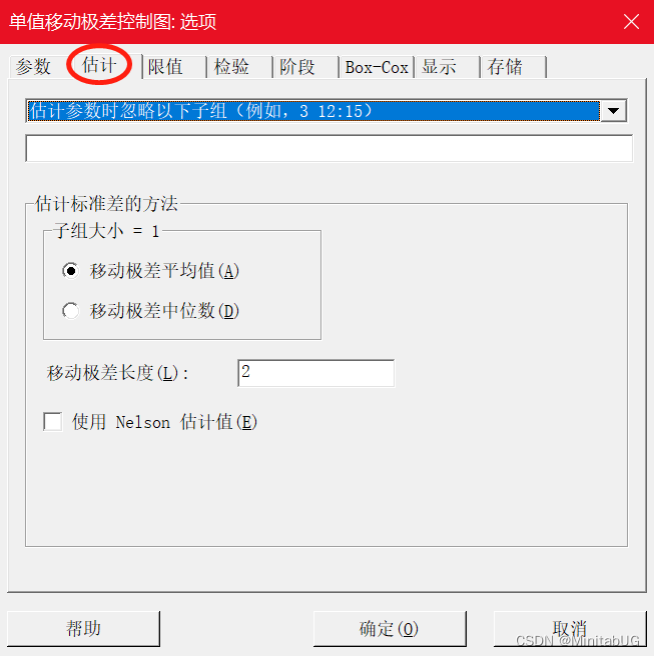
1）移动极差平均值（默认方法）-移动极差长度默认为 2

a. 计算移动极差 MR（相邻 2 个数的较大值减较小值），当前数据样本量为 25，计算得到

24 个移动极差。

b. 计算这 24 个移动极差的平均值 MRbar

c. 估计标准差的公式如下：

控制限计算公式

𝑳𝑪𝑳 = 𝒖 − 𝒌𝜹

𝑼𝑪𝑳 = 𝒖 + 𝒌𝜹

其中 k 为检验 1 的参数。默认值为 3。

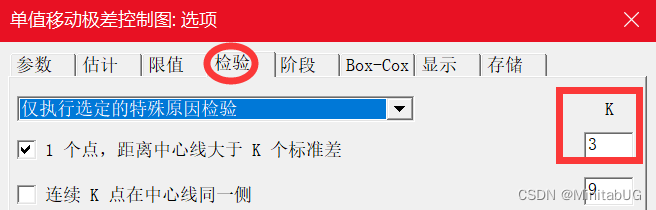
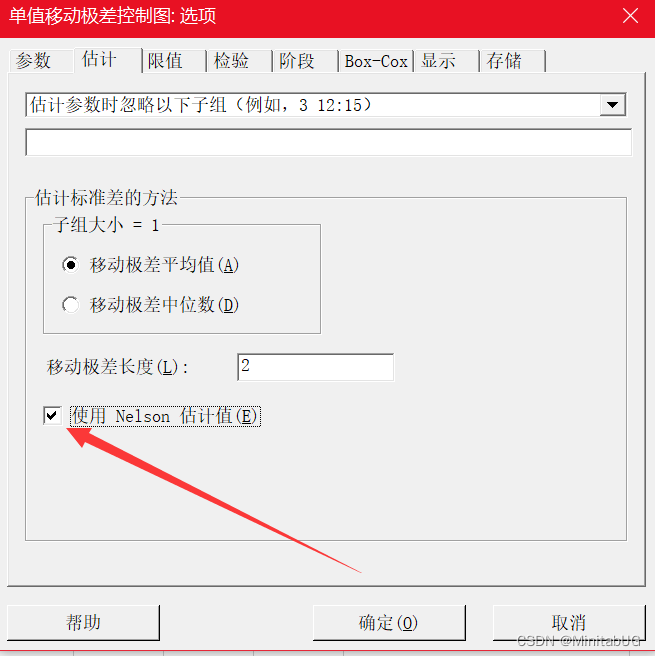
当选择默认的用移动极差平均值来估计标准差时，我们还可以勾选”使用 Nelson 估计值”。

使用 Nelson 估计值可以在计算控制限时更正异常大的移动极差值。此过程与 Nelson1 提

出的过程相似。Minitab 消除比移动极差平均值大 3σ 的任何移动极差值，然后重新计算移

动极差平均值和控制限。

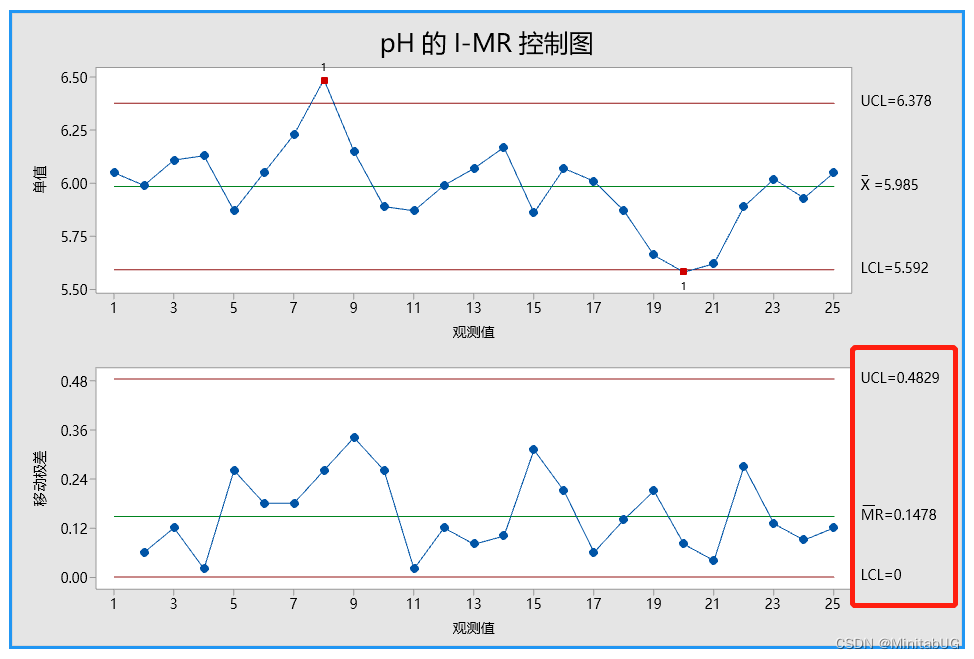
2）移动极差中位数

a. 计算移动极差

b. 计算移动极差中位数

c. 估计标准差的公式如下：

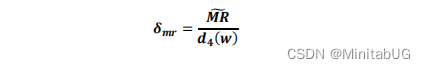
二、移动极差控制图（MR 控制图）

X 轴：批次 ID

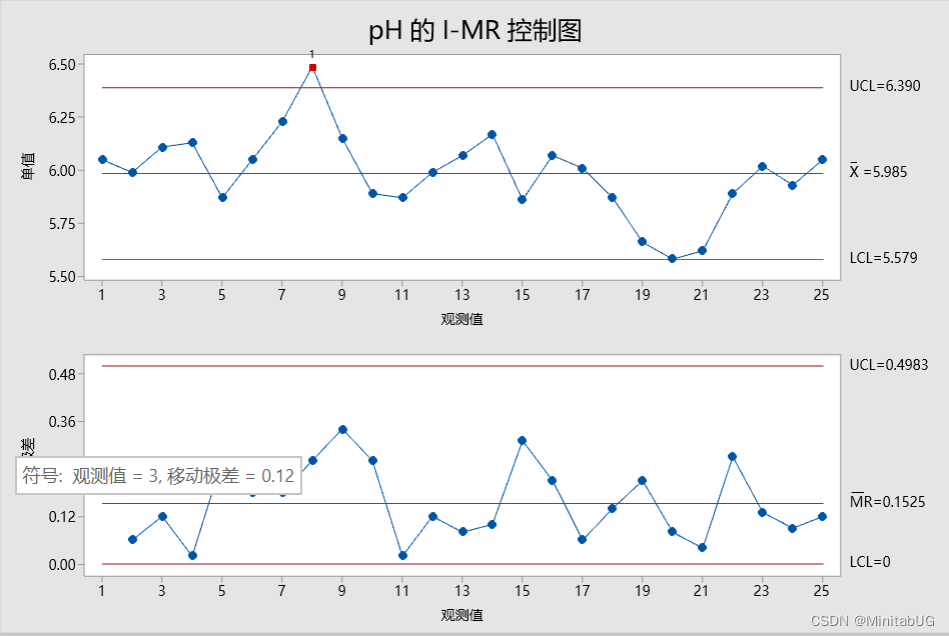
Y 轴：移动极差（如下 MR 控制图中的第二个点是批次 2 的 pH 值 5.99 和批次 3pH 值 6.11

中较大值减去较小值，结果为 0.12（6.11-5.99）

点：MR 控制图上的标绘点是移动极差（移动极差是两个或多个连续

点之间差值的绝对值）。

中心线：中心线是移动极差平均值的无偏估计值 MRbar

控制上限：𝑼𝑪𝑳 = (𝒅𝟐 (𝒘) ⋅ 𝜹) + (𝒌 ⋅ 𝒅𝟑 (𝒘) ⋅ 𝜹)

控制下限：𝑳𝑪𝑳 = (𝒅𝟐 (𝒘) ⋅ 𝜹) − (𝒌 ⋅ 𝒅𝟑 (𝒘) ⋅ 𝜹)或 LCL=0（计算结果

为负值时）

移动极差平均值法的结果

移动极差中位数法的结果

结论

手动计算的过程比较复杂，而且还可能会出错，但是有了 Minitab 的帮助，我们只需要选择

好合适的控制图后，点击几下就可以高效快速的计算出对应的控制限。当然，花点时间手动

计算一下这些值，能够帮助你更好的理解控制图。而且在计算的过程中，你也会发现 Minitab

的算法跟 Excel 中算法的差异，也能够发现单值控制图的控制限受到移动极差的影响，所以

在分析这两张控制图时，应该先分析下面的移动极差控制图，移动极差控制图中没有异常点

时，这时候分析单值控制图才是有意义的。

X 轴：批次 ID

Y 轴：移动极差（如下 MR 控制图中的第二个点是批次 2 的 pH 值 5.99 和批次

3pH 值 6.11 中较大值减去较小值，结果为 0.12（6.11-5.99）