目录
- 0 专栏介绍
- 1 什么是Dubins曲线?
- 2 Dubins曲线原理
- 2.1 坐标变换
- 2.2 单步运动公式
- 2.3 曲线模式
- 3 Dubins曲线生成算法
- 4 仿真实现
- 4.1 ROS C++实现
- 4.2 Python实现
- 4.3 Matlab实现
0 专栏介绍
🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);曲线优化(贝塞尔曲线、B样条曲线等)。
🚀详情:图解自动驾驶中的运动规划(Motion Planning),附几十种规划算法
1 什么是Dubins曲线?
Dubins曲线是指由美国数学家 Lester Dubins 在20世纪50年代提出的一种特殊类型的最短路径曲线。这种曲线通常用于描述在给定转弯半径下的无人机、汽车或船只等载具的最短路径,其特点是起始点和终点处的切线方向和曲率都是已知的。

Dubins曲线包括直线段和最大转弯半径下的圆弧组成,通过合适的组合可以实现从一个姿态到另一个姿态的最短路径规划。这种曲线在航空、航海、自动驾驶等领域具有广泛的应用,能够有效地规划航行路径,减少能量消耗并提高效率。
2 Dubins曲线原理
2.1 坐标变换
如图所示,在全局坐标系 x O y xOy xOy中,设机器人起始位姿、终止位姿、最小转弯半径分别为 ( x s , y s , α ) \left( x_s,y_s,\alpha \right) (xs,ys,α)、 ( x g , y g , β ) \left( x_g,y_g,\beta \right) (xg,yg,β)与 R R R,则以 p s = ( x s , y s ) \boldsymbol{p}_s=\left( x_s,y_s \right) ps=(xs,ys)为新坐标系原点, p s \boldsymbol{p}_s ps指向 p g = ( x g , y g ) \boldsymbol{p}_g=\left( x_g,y_g \right) pg=(xg,yg)方向为 x ′ x' x′轴,垂直方向为 y ′ y' y′轴建立新坐标系 x ′ O ′ y ′ x'O'y' x′O′y′。
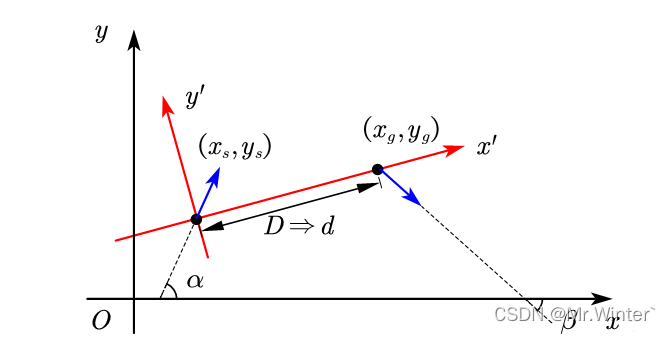
根据比例关系 d / D = r / R {{d}/{D}}={{r}/{R}} d/D=r/R,其中 D = ∥ p s − p g ∥ 2 D=\left\| \boldsymbol{p}_s-\boldsymbol{p}_g \right\| _2 D= ps−pg 2。为了便于后续推导,不妨归一化最小转弯半径,即令 r = 1 r=1 r=1。所以在坐标系 x ′ O ′ y ′ x'O'y' x′O′y′中,通常取起点、终点间距为 d = D / R d={{D}/{R}} d=D/R,从而起始位姿、终止位姿、最小转弯半径分别转换为
s t a r t = [ 0 0 α − θ ] T , g o a l = [ d 0 β − θ ] T , r = 1 \mathrm{start}=\left[ \begin{matrix} 0& 0& \alpha -\theta\\\end{matrix} \right] ^T, \mathrm{goal}=\left[ \begin{matrix} d& 0& \beta -\theta\\\end{matrix} \right] ^T, r=1 start=[00α−θ]T,goal=[d0β−θ]T,r=1
其中 θ = a r c tan ( ( y g − y s ) / ( x g − x s ) ) \theta =\mathrm{arc}\tan \left( {{\left( y_g-y_s \right)}/{\left( x_g-x_s \right)}} \right) θ=arctan((yg−ys)/(xg−xs)),接下来的推导均基于转换坐标系 x ′ O ′ y ′ x'O'y' x′O′y′。
2.2 单步运动公式
对于直行运动,设沿直线行进距离为 l l l,则
[ x ∗ y ∗ ϕ ∗ ] T = [ x + l cos ϕ y + l sin ϕ ϕ ] T \left[ \begin{matrix} x^*& y^*& \phi ^*\\\end{matrix} \right] ^T=\left[ \begin{matrix} x+l\cos \phi& y+l\sin \phi& \phi\\\end{matrix} \right] ^T [x∗y∗ϕ∗]T=[x+lcosϕy+lsinϕϕ]T
对于转弯运动,假设转向角为 ψ \psi ψ,则由弧长公式可得
l = ψ r = r = 1 ψ l=\psi r\xlongequal{r=1}\psi l=ψrr=1ψ
因此设沿圆弧行进距离为 l l l,以左转为例,由几何关系易得
[ x ∗ y ∗ ϕ ∗ ] T = [ x + r sin ( ϕ + ψ ) − r sin ( ϕ ) y + r cos ( ϕ + ψ ) + r cos ( ϕ ) ϕ + ψ ] T \left[ \begin{matrix} x^*& y^*& \phi ^*\\\end{matrix} \right] ^T=\left[ \begin{matrix} x+r\sin \left( \phi +\psi \right) -r\sin \left( \phi \right)& y+r\cos \left( \phi +\psi \right) +r\cos \left( \phi \right)& \phi +\psi\\\end{matrix} \right] ^T [x∗y∗ϕ∗]T=[x+rsin(ϕ+ψ)−rsin(ϕ)y+rcos(ϕ+ψ)+rcos(ϕ)ϕ+ψ]T
代入 r = 1 r=1 r=1、 ψ = l \psi=l ψ=l可得
[ x ∗ y ∗ ϕ ∗ ] T = [ x + sin ( ϕ + l ) − sin ( ϕ ) y + cos ( ϕ + l ) + cos ( ϕ ) ϕ + l ] T \left[ \begin{matrix} x^*& y^*& \phi ^*\\\end{matrix} \right] ^T=\left[ \begin{matrix} x+\sin \left( \phi +l \right) -\sin \left( \phi \right)& y+\cos \left( \phi +l \right) +\cos \left( \phi \right)& \phi +l\\\end{matrix} \right] ^T [x∗y∗ϕ∗]T=[x+sin(ϕ+l)−sin(ϕ)y+cos(ϕ+l)+cos(ϕ)ϕ+l]T
同理,对于右转而言,有
[ x ∗ y ∗ ϕ ∗ ] T = [ x − sin ( ϕ − l ) + sin ( ϕ ) y + cos ( ϕ + l ) − cos ( ϕ ) ϕ − l ] T \left[ \begin{matrix} x^*& y^*& \phi ^*\\\end{matrix} \right] ^T=\left[ \begin{matrix} x-\sin \left( \phi -l \right) +\sin \left( \phi \right)& y+\cos \left( \phi +l \right) -\cos \left( \phi \right)& \phi -l\\\end{matrix} \right] ^T [x∗y∗ϕ∗]T=[x−sin(ϕ−l)+sin(ϕ)y+cos(ϕ+l)−cos(ϕ)ϕ−l]T
综上所述,可得单步运动映射
{ L l + ( x , y , ϕ ) = [ x + sin ( ϕ + l ) − sin ( ϕ ) y − cos ( ϕ + l ) + cos ( ϕ ) ϕ + l ] T R l + ( x , y , ϕ ) = [ x − sin ( ϕ − l ) + sin ( ϕ ) y + cos ( ϕ − l ) − cos ( ϕ ) ϕ − l ] T S l + ( x , y , ϕ ) = [ x + l cos ϕ y + l sin ϕ ϕ ] T \begin{cases} L_{l}^{+}\left( x,y,\phi \right) =\left[ \begin{matrix} x+\sin \left( \phi +l \right) -\sin \left( \phi \right)& y-\cos \left( \phi +l \right) +\cos \left( \phi \right)& \phi +l\\\end{matrix} \right] ^T\\ R_{l}^{+}\left( x,y,\phi \right) =\left[ \begin{matrix} x-\sin \left( \phi -l \right) +\sin \left( \phi \right)& y+\cos \left( \phi -l \right) -\cos \left( \phi \right)& \phi -l\\\end{matrix} \right] ^T\\ S_{l}^{+}\left( x,y,\phi \right) =\left[ \begin{matrix} x+l\cos \phi& y+l\sin \phi& \phi\\\end{matrix} \right] ^T\\\end{cases} ⎩ ⎨ ⎧Ll+(x,y,ϕ)=[x+sin(ϕ+l)−sin(ϕ)y−cos(ϕ+l)+cos(ϕ)ϕ+l]TRl+(x,y,ϕ)=[x−sin(ϕ−l)+sin(ϕ)y+cos(ϕ−l)−cos(ϕ)ϕ−l]TSl+(x,y,ϕ)=[x+lcosϕy+lsinϕϕ]T
2.3 曲线模式
Dubins曲线假设物体只能向前,通过组合左转、右转、直行可得六种运动模式
{ L S L , R S R , R S L , L S R , R L R , L R L } \left\{ LSL, RSR, RSL, LSR, RLR, LRL \right\} {LSL,RSR,RSL,LSR,RLR,LRL}
可以总结这六种运动模式的解析解为


3 Dubins曲线生成算法
Dubins曲线路径生成算法流程如表所示

4 仿真实现
4.1 ROS C++实现
核心代码如下所示
Points2d Dubins::generation(Pose2d start, Pose2d goal)
{Points2d path;double sx, sy, syaw;double gx, gy, gyaw;std::tie(sx, sy, syaw) = start;std::tie(gx, gy, gyaw) = goal;// coordinate transformationgx -= sx;gy -= sy;double theta = helper::mod2pi(atan2(gy, gx));double dist = hypot(gx, gy) * max_curv_;double alpha = helper::mod2pi(syaw - theta);double beta = helper::mod2pi(gyaw - theta);// select the best motionDubinsMode best_mode;double best_cost = DUBINS_MAX;DubinsLength length;DubinsLength best_length = { DUBINS_NONE, DUBINS_NONE, DUBINS_NONE };DubinsMode mode;for (const auto solver : dubins_solvers){(this->*solver)(alpha, beta, dist, length, mode);_update(length, mode, best_length, best_mode, best_cost);}if (best_cost == DUBINS_MAX)return path;// interpolation...// coordinate transformationEigen::AngleAxisd r_vec(theta, Eigen::Vector3d(0, 0, 1));Eigen::Matrix3d R = r_vec.toRotationMatrix();Eigen::MatrixXd P = Eigen::MatrixXd::Ones(3, path_x.size());for (size_t i = 0; i < path_x.size(); i++){P(0, i) = path_x[i];P(1, i) = path_y[i];}P = R * P;for (size_t i = 0; i < path_x.size(); i++)path.push_back({ P(0, i) + sx, P(1, i) + sy });return path;
}
4.2 Python实现
核心代码如下所示
def generation(self, start_pose: tuple, goal_pose: tuple):sx, sy, syaw = start_posegx, gy, gyaw = goal_pose# coordinate transformationgx, gy = gx - sx, gy - sytheta = self.mod2pi(math.atan2(gy, gx))dist = math.hypot(gx, gy) * self.max_curvalpha = self.mod2pi(syaw - theta)beta = self.mod2pi(gyaw - theta)# select the best motionplanners = [self.LSL, self.RSR, self.LSR, self.RSL, self.RLR, self.LRL]best_t, best_p, best_q, best_mode, best_cost = None, None, None, None, float("inf")for planner in planners:t, p, q, mode = planner(alpha, beta, dist)if t is None:continuecost = (abs(t) + abs(p) + abs(q))if best_cost > cost:best_t, best_p, best_q, best_mode, best_cost = t, p, q, mode, cost# interpolation...# coordinate transformationrot = Rot.from_euler('z', theta).as_matrix()[0:2, 0:2]converted_xy = rot @ np.stack([x_list, y_list])x_list = converted_xy[0, :] + sxy_list = converted_xy[1, :] + syyaw_list = [self.pi2pi(i_yaw + theta) for i_yaw in yaw_list]return best_cost, best_mode, x_list, y_list, yaw_list
4.3 Matlab实现
核心代码如下所示
function [x_list, y_list, yaw_list] = generation(start_pose, goal_pose, param)sx = start_pose(1); sy = start_pose(2); syaw = start_pose(3);gx = goal_pose(1); gy = goal_pose(2); gyaw = goal_pose(3);% coordinate transformationgx = gx - sx; gy = gy - sy;theta = mod2pi(atan2(gy, gx));dist = hypot(gx, gy) * param.max_curv;alpha = mod2pi(syaw - theta);beta = mod2pi(gyaw - theta);% select the best motionplanners = ["LSL", "RSR", "LSR", "RSL", "RLR", "LRL"];best_cost = inf;best_segs = [];best_mode = [];for i=1:length(planners)planner = str2func(planners(i));[segs, mode] = planner(alpha, beta, dist);if isempty(segs)continueendcost = (abs(segs(1)) + abs(segs(2)) + abs(segs(3)));if best_cost > costbest_segs = segs;best_mode = mode;best_cost = cost;endend% interpolation...% coordinate transformationrot = [cos(theta), -sin(theta); sin(theta), cos(theta)];converted_xy = rot * [x_list; y_list];x_list = converted_xy(1, :) + sx;y_list = converted_xy(2, :) + sy;for j=1:length(yaw_list)yaw_list(j) = pi2pi(yaw_list(j) + theta);end
end

完整工程代码请联系下方博主名片获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …







)





![[linux] matplotlib plt画training dynamics指标曲线时,标记每个点的值](http://pic.xiahunao.cn/[linux] matplotlib plt画training dynamics指标曲线时,标记每个点的值)




