目录
1 基于Logistic函数的负荷转移率模型
2 程序示例
3 效果图
4 下载链接
负荷需求响应模型种类较多,有电价型和激励型等类型,本次和大家分享一个基于Logistic函数的负荷转移率模型,该模型属于电价型,由于该方法使用的较少,从创新方面给了大家更广阔的空间。
1 基于Logistic函数的负荷转移率模型
由消费者心理学可知,电价差过大、过小以及在电价差变化处响应度曲线平滑性,均会引起用户需求响应的变化。在电价激励机制下,用户本着自愿原则,其响应行为具有明显的随机性,则真实需求响应曲线会处于乐观与悲观响应预测曲线之间,具备模糊属性。如图 2-5 所示,以峰谷负荷转移为例,建立了基于 Logistic 函数的模糊响应机理,图中 Δppv 表示峰谷时段电价差,λpv 表示峰转谷负荷转移率,即在某时段峰转谷的负荷量与峰时段平均用电量比值,从而体现用户对不同电价的响应程度。该模型划分了“死区”、“响应区”和“饱和区”。在“死区”,由于电价差过小,未能引发用户自主调整用电模式;在“响应区”,随着电价差增大,用户响应积极性被调动;在“饱和区”,虽然电价差很大,但已完全挖掘用户负荷弹性潜力,因此负荷转移率值达到极限。另外,当电价差为 0 时,即未采用分时电价,此时用户响应行为具有很强的随机性,甚至负荷转移率出现负值的情况。

基于上述模型,为提高实际情况下分时电价因素对负荷曲线拟合的精度,Logistic 函数利用可变参数,增加负荷转移率变化的跨度,其函数模型如式

在式(2-11)中 a 表示函数值范围,c 为 a/2+b 函数值所对应的横坐标,近似表示“响应区”电价差的中点,b 用于上下平移函数曲线。基于上述公式,即可提高乐观和悲观响应预测曲线的拟合精度,从而反映分时电价对用户实际响应机理模型的影响。因此,为提高模型精度,本节通过用户响应随机性和乐观响应隶属度两个指标对实际用户响应机理模型进行概率约束。如图 2-6 所示,在“死区”,电价差过小,用户响应行为具有很强的随机性,故由乐观和悲观响应预测的平均值确定。在“响应区”,用户响应行为明显,且响应行为更倾向于乐观响应预测曲线。因此需考虑采用偏大型半梯形隶属度函数计算乐观响应隶属度,并将其作为需求响应机理的概率约束。在“饱和区”,由于两种曲线重合,用户响应行为即可用负荷转移率最大值表示。具体计算公式如(2-12)、(2-13)所示。




2 程序示例
程序示例给出峰谷负荷转移率计算程序,如下所示。
jf=0.8118;%峰段电价jg=0.4438;%谷段电价jp=0.5713;%平段电价dj=[jg.*ones(1,7) jf.*ones(1,7) jg.*ones(1,4) jf.*ones(1,4) jp.*ones(1,2)];%电价情况pload1=[270 225 215 230 245 295 400 425 475 500 560 575 577.5 527.5 450 350 375 450 525 575 600 575 500 425]./20;%负荷detap=jf-jg;%峰谷价差lammax=al/(1+exp(-(detap-cl)/ul))+bl;%乐观负荷转移率lammin=ab/(1+exp(-(detap-cb)/ul))+bb;%悲观负荷转移率mpv=(jf-jg-apv)/(bpv-apv);%乐观响应隶属度detapv=jf-jg;%峰谷价差if detapv<=apv%不同情况下的转移率lambpv=(lammax+lammin)/2;elseif detapv<=bpvlambpv=lammin+(lammax+lammin)/2*(1+mpv);elselambpv=lammax;end
程序还需要根据上述编写平-谷、峰-平的程序段,构成完整程序后可运行得到下面的结果。
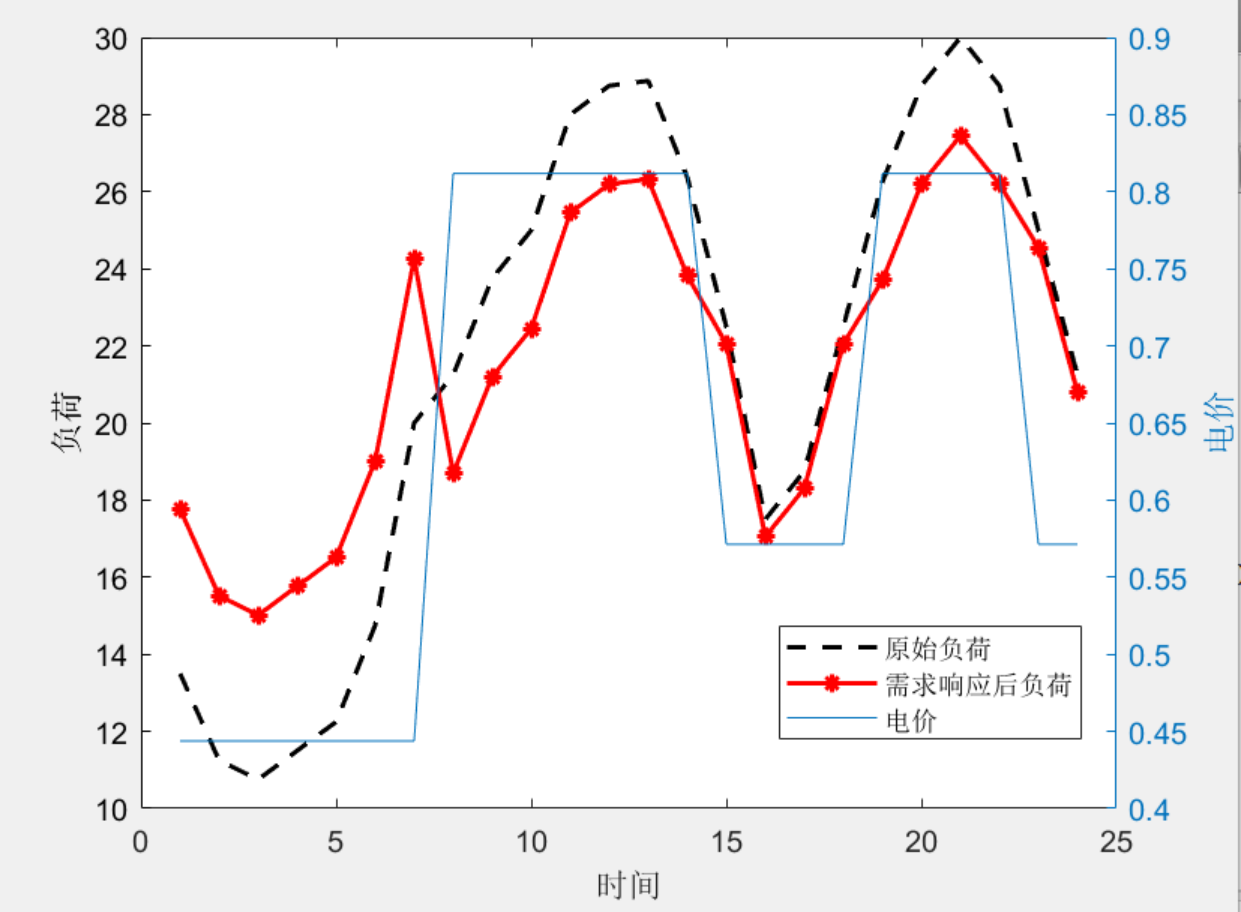
3 效果图
- 运行程序可以得到如下的效果图。



![[linux] matplotlib plt画training dynamics指标曲线时,标记每个点的值](http://pic.xiahunao.cn/[linux] matplotlib plt画training dynamics指标曲线时,标记每个点的值)










)

)

