一.最长上升子序列（LIS）的相关知识

1.最长上升子序列（Longest  Increasing Subsequence），简称LIS，也有些情况求的是最长非降序子序列，二者区别就是序列中是否可以有相等的数。假设我们有一个序列 b i，当b1 < b2 < … < bS的时候，我们称这个序列是上升的。

（或许我们刚开始对于这样的名词感到陌生，对于解释也不理解，那我们就要知道它的前置知识）

 一.什么是子序列？

    一个序列A={a1,a2,...an}中任意删除若干项，剩余的序列叫做A的一个子序列。例如序列A={1,3,5,4,2}，删除其中的第3项和第5项，得到序列B={1,3,4}，删除其中的第3项和第4项，得到序列C={1，3，2}，此时序列B和C是序列A的子序列。

二.什么是最长子序列？

    如果序列中的元素是从小到大排列的，则该序列为上升序列，如果该序列又是其它序列的子序列，则称为上升子序列。例如“1.1 子序列”中提到的B是A的上升子序列，而C是A的子序列，但不是上升子序列。

了解这两个前置知识，那么最长上升子序列就很容易理解了。

即包含元素最多的上升子序列，叫做最长上升子序列。

 

 二.LIS长度的求解方法

一.方法一：动态规划（O(n^2)朴素法）

动态规划的一个特点就是当前解可以由上一个阶段的解推出， 由此，把我们要求的问题简化成一个更小的子问题。我们求最长上升子序列也符合这一特点，我们要求前n个数的最长上升子序列就是可以转换成求前n-1个数的最长上升子序列......这样逐步分解，直到求前1个数的最长上升子序列。

状态转移方程为：dp[i]=max(dp[i],dp[j]+1)

其核心代码段为：

for (int i = 1; i <= n; i++) {for (int j = 1; j < i; j++) {if (a[i] > a[j])dp[i] = max(dp[i], dp[j] + 1);}}for (int i = 1; i <= n; i++) {ans = max(ans, dp[i]);}

---

 

二.方法二：贪心+二分（O(nlogn)）

用一个low数组记录长度，low[i]表示长度都为i的LIS结尾元素的最小值，这样我们在记录low的时候，当a[i]大于low[++当前LIS最大长度]时候，直接将a[i]接在low中，否则在low中二分查找大于等于当前元素a[i]的第一个位置pos，用a[i]替换掉之前的low[pos].最后我们找一下最长上升子序列下标满足的解，记录下该子序列即可.(注意，low数组不一定是最长上升子序列，只是长度对等)

这里的二分操作可以用STL中的lower_bound（）函数实现。

核心代码段：

low[++sum]=a[1];
for (int i = 2; i <= n; i++) {if (a[i] > low[sum])low[++sum] = a[i];else{int k = lower_bound(low + 1, low + sum + 1, a[i]) - dp;low[k] = a[i];}
}

 

三.例题分析

 一.B3637 最长上升子序列

 

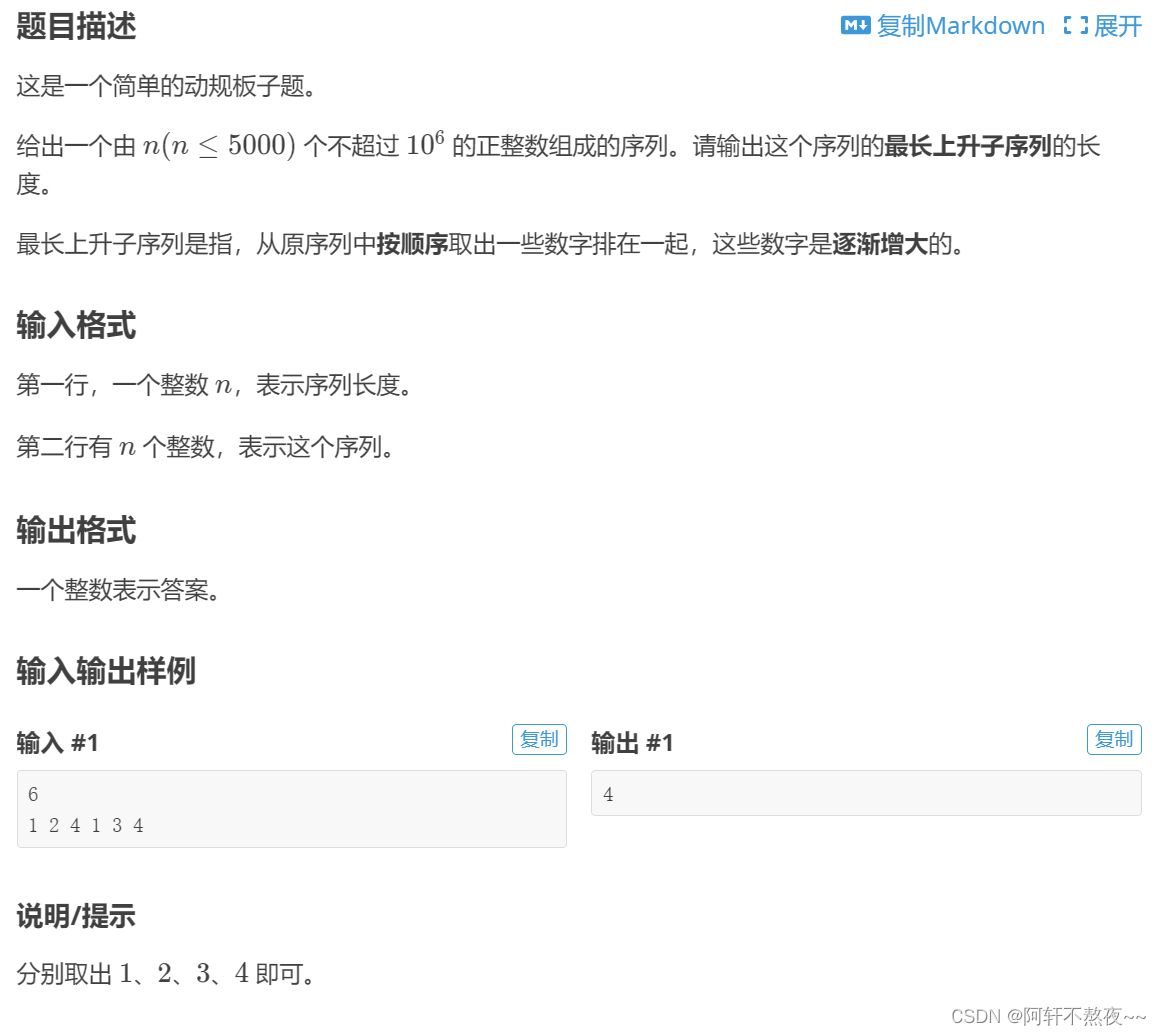
 这一题就相当于最长上升子序列的模版题，通过动态规划（朴素法）就可以解决，这里可以当做模版学习。

#include<bits/stdc++.h>
using namespace std;
#define N 1000005
int dp[N], a[N];
int ans, n, m, sum;
int main()
{cin >> n;for (int i = 1; i <= n; i++) {cin >> a[i];dp[i] = 1;           //初始化，dp都为1，即自身是一个上升子序列}for (int i = 1; i <= n; i++) {for (int j = 1; j < i; j++) {  //如果在之前的序列有小于a[i]的，更新dpif (a[i] > a[j])dp[i] = max(dp[i], dp[j] + 1);}}for (int i = 1; i <= n; i++) {ans = max(ans, dp[i]);   //找出最长的上升子序列}cout << ans << endl;return 0;
}

二.LIS

这一题和刚刚的题目的意思是一模一样的，唯一的区别就是数据范围变大了，变为1e5，如果我们还是和刚刚一样使用O(n^2)的方法，肯定会超时，那么我们就应该使用方法二：贪心+二分       （O（nlogn））

#include<bits/stdc++.h>
using namespace std;
#define N 100005
int a[N], b[N];
int n, m, sum, ans;
int main()
{cin >> n;for (int i = 1; i <= n; i++) {cin >> a[i];}b[++sum] = a[1];     //核心代码段，没什么好说的for (int i = 2; i <= n; i++) {if (a[i] > b[sum])b[++sum] = a[i];else{int k = lower_bound(b + 1, b + sum + 1, a[i]) - b;b[k] = a[i];}}cout << sum << endl;return 0;
}

这里给大家留下两道练习题，这两道题都是在此基础上的变形题，可以会有点难（都是洛谷上的题，可以看题解），后面我也会给出分析。

[ARC149B] Two LIS Sum

P8736 [蓝桥杯 2020 国 B] 游园安排

另外，关于LIS还有一个姊妹叫作LCS（最长公共上上子序列），下次我们将讲解相关内容，好了今天的内容就到这里了。~QVQ~