盒模型的宽度计算

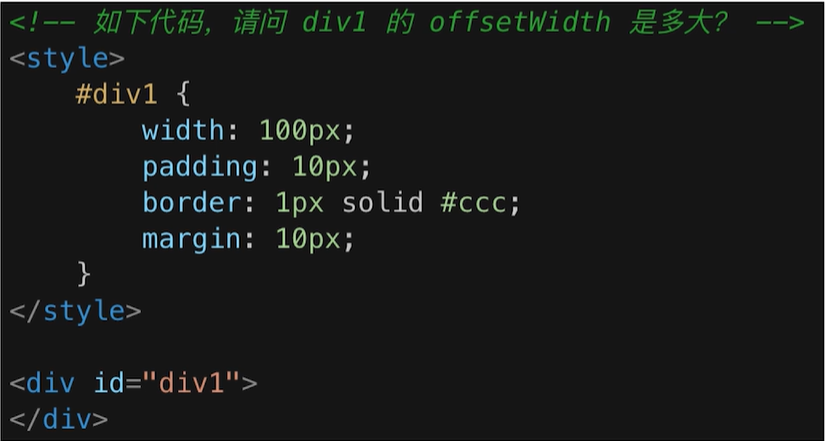
默认为标准盒模型 box-sizing:content-box;
offsetWidth =(内容宽度+内边距 +边框)，无外边距

答案 122px

通过 box-sizing: border-box; 可切换为 IE盒模型
offsetWidth = width 即 100px

margin 纵向重叠

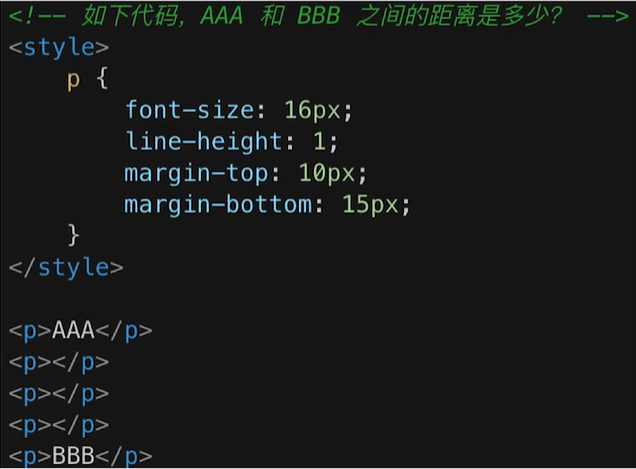
• 相邻元素的 margin-top 和 margin-bottom 会发生重叠
• 空白内容的 <p></p>也会重叠，相当于不存在

答案 15px

margin 设置负值

• margin-top 负值，元素向上移动
• margin-left 负值，元素向左移动
• margin-right 负值，右侧元素左移，自身不受影响
• margin-bottom 负值，下方元素上移，自身不受影响

line-height 的继承

答案 40px

• 值为具体数值，如 30px，则继承该值，子元素的 line-height 也是 30px
• 值为比例，如2或1.5，则继承该比例，子元素的 line-height 也是 2或1.5
• 【考点】值为百分比，如 200%，则继承父元素计算后的值，此题中 body 的 line-height 计算后的值是 40px，所以子元素的 line-height 应该是 40px