探索Manticore Search：开源全文搜索引擎的强大功能

在当今信息爆炸的时代，数据的快速检索变得至关重要。无论是在电子商务网站、新闻门户还是企业内部文档，高效的搜索引擎都是确保用户满意度和工作效率的关键因素之一。而在搜索引擎领域，Manticore Search 作为一款开源的全文搜索引擎，正在吸引越来越多的关注。本文将探讨 Manticore Search 的功能特性以及为什么它成为许多企业和开发者的首选工具。

介绍Manticore Search

Manticore Search 是一个基于开源的高性能全文搜索引擎，最初是作为 Sphinx 搜索引擎的分支而开发的。它支持全文搜索、实时索引、分布式搜索等功能，并且具有出色的性能和灵活的配置选项。作为一款功能强大的搜索引擎，Manticore Search 在许多不同的应用场景下都得到了广泛的应用，包括电子商务、新闻发布、知识管理和日志分析等。

主要功能特性

1. 实时索引

Manticore Search 提供了实时索引功能，允许用户对数据进行实时索引和搜索。这意味着当数据发生变化时，索引会立即更新，用户可以立即搜索到最新的结果。这对于需要实时分析和检索数据的应用非常有用，比如监控日志、即时通讯等场景。

2. 分布式搜索

Manticore Search 支持分布式搜索，可以轻松地扩展到多个节点，实现水平扩展和负载均衡。这使得它能够处理大规模的数据，并且在高并发情况下保持稳定的性能。通过分布式搜索，用户可以构建强大的搜索集群，以满足不同规模和需求的应用。

3. 多种数据源支持

Manticore Search 支持多种数据源的索引，包括关系型数据库、文档数据库、JSON 数据等。这使得用户可以轻松地将现有的数据集成到搜索引擎中，无需进行繁琐的数据转换和迁移。

4. 强大的查询语言

Manticore Search 提供了丰富和灵活的查询语言，支持复杂的查询操作和条件筛选。用户可以通过查询语言来实现高级搜索功能，比如布尔搜索、范围搜索、排序、过滤等。同时，它还支持自定义插件和扩展，可以根据需要进行定制和扩展。

5. 高性能和低资源消耗

Manticore Search 具有出色的性能和低资源消耗的特点，能够在较低的硬件配置下提供高效的搜索服务。它采用了先进的索引和搜索算法，优化了内存和CPU的使用，同时还支持多线程和并行搜索，以实现更快的搜索速度和更高的并发性能。

结语

总的来说，Manticore Search 是一款功能强大、性能优异的开源全文搜索引擎，适用于各种不同规模和需求的应用场景。它提供了丰富的功能特性和灵活的配置选项，可以帮助用户快速构建高效的搜索服务。无论是在电子商务、新闻发布、知识管理还是日志分析等领域，Manticore Search 都是一个值得考虑的选择。通过不断的更新和改进，相信它将会在搜索引擎领域发挥越来越重要的作用。

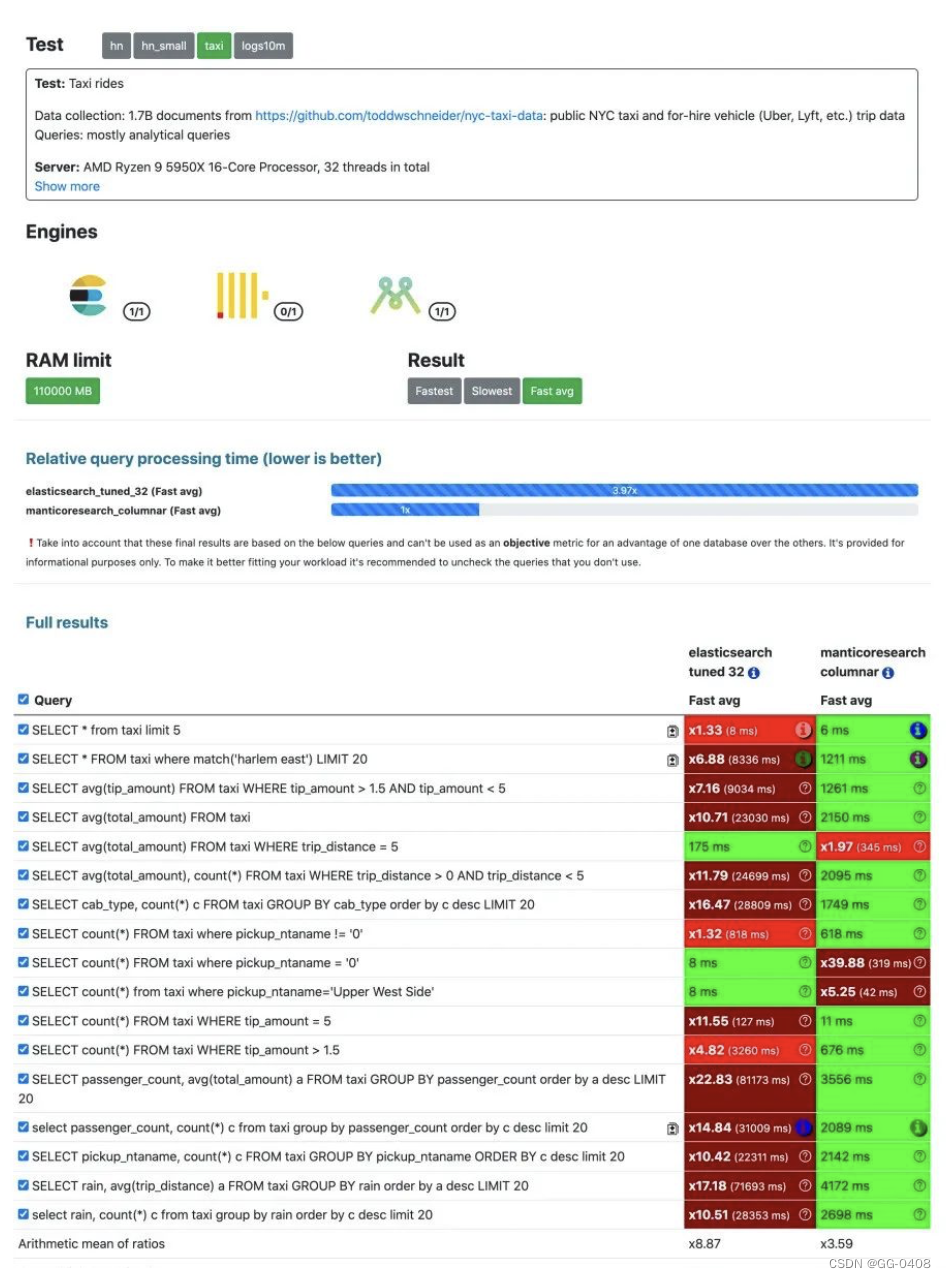
在特定的场景下速度更是要比ES快出10余倍

https://manticoresearch.com/blog/manticore-alternative-to-elasticsearch/

Docker 镜像可在Docker Hub上获取：

https://hub.docker.com/r/manticoresearch/manticore/

要在 Docker 中试验 Manticore Search，只需运行：

docker run -e EXTRA=1 --name manticore --rm -d manticoresearch/manticore && until docker logs manticore 2>&1 | grep -q "accepting connections"; do sleep 1; done && docker exec -it manticore mysql && docker stop manticore

之后，可以进行其他操作，例如创建表、添加数据并运行搜索：

create table movies(title text, year int) morphology='stem_en' html_strip='1' stopwords='en';insert into movies(title, year) values ('The Seven Samurai', 1954), ('Bonnie and Clyde', 1954), ('Reservoir Dogs', 1992), ('Airplane!', 1980), ('Raging Bull', 1980), ('Groundhog Day', 1993), ('<a href="http://google.com/">Jurassic Park</a>', 1993), ('Ferris Bueller\'s Day Off', 1986);select highlight(), year from movies where match('the dog');select highlight(), year from movies where match('days') facet year;select * from movies where match('google');

完整文档和开源代码，可以移步：