目录
一、基于采样的规划方法概述
二、概率路图（PRM）
1、核心思想
2、实现流程
3、算法描述
4、节点连接处理
5、总结
三、快速搜索随机树（RRT）
1、核心思想
2、实现流程
3、总结
4、改进RRT算法
①快速搜索随机图（RRG）
②基于运动学的快速搜索随机树（Kinematic-based RRT）
一、基于采样的规划方法概述
基于采样的方法就是在状态空间中不断地随机撒点，将这些节点根据一定的规则与周围的节点进行连接，以此构造一条条局部路径，最终找到一条从起点到终点的路径。随着采样点的不断增多，最终得到的解会不断逼近最优解。
一般步骤：
- 为图表添加随机数种子
- 以某种策略或者给定条件采样到起始节点
- 选择和哪些其他节点进行连接
- 选择添加或者移除哪些边
二、概率路图（PRM）
1、核心思想
PRM有两个阶段分别是学习阶段（Learning Phase）和查询阶段（Query Phase）。
学习阶段：
- 在配置空间中随机采样足够数量的点；
- 将相互之间能够到达的节点进行连接。
查询阶段：
- 利用图搜索算法寻找图表中从起始节点到目标节点的路径。
2、实现流程
（a）图中所示为一个用于采样的配置空间，在配置空间中，自动驾驶车辆可以被近似看成一个质点，环境中的障碍物等信息都被近似为图中的forbidden space，自动驾驶车辆在free space空间中运动，二无需考虑其几何形状和运动状态；
（b）图中通过随机采样的方式获得一个坐标点，采样的方法也要根据特定的场景做出不同的选择，常见的采样算法有均匀分布采样（在未知场景中采样）、高斯分布采样（在自动驾驶场景中通常以车道中心线为均值）等；
（c）图中通过采样大量的点来获取地图的形状；
（d）图中对采样点进行碰撞检验，删除forbidden space中的采样点；
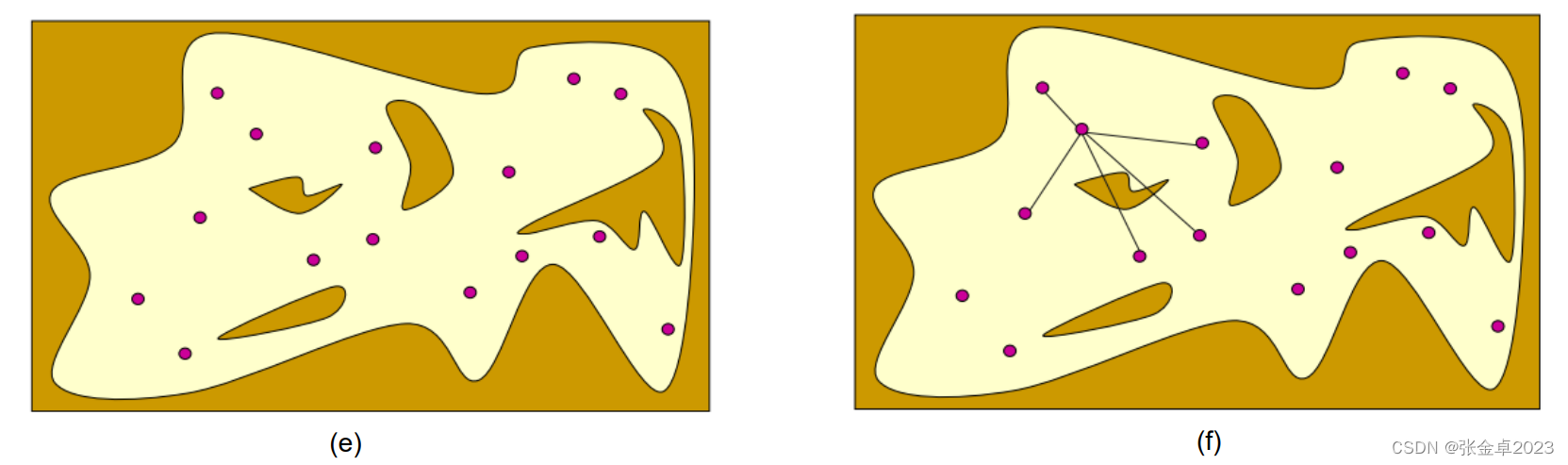
（e）图中为删除forbiden space中的采样点后，在free space中保留下来的有效采样点；
（f）图中每个有效采样点会连接以当前节点为圆心，半径r圆形范围内的所有采样点
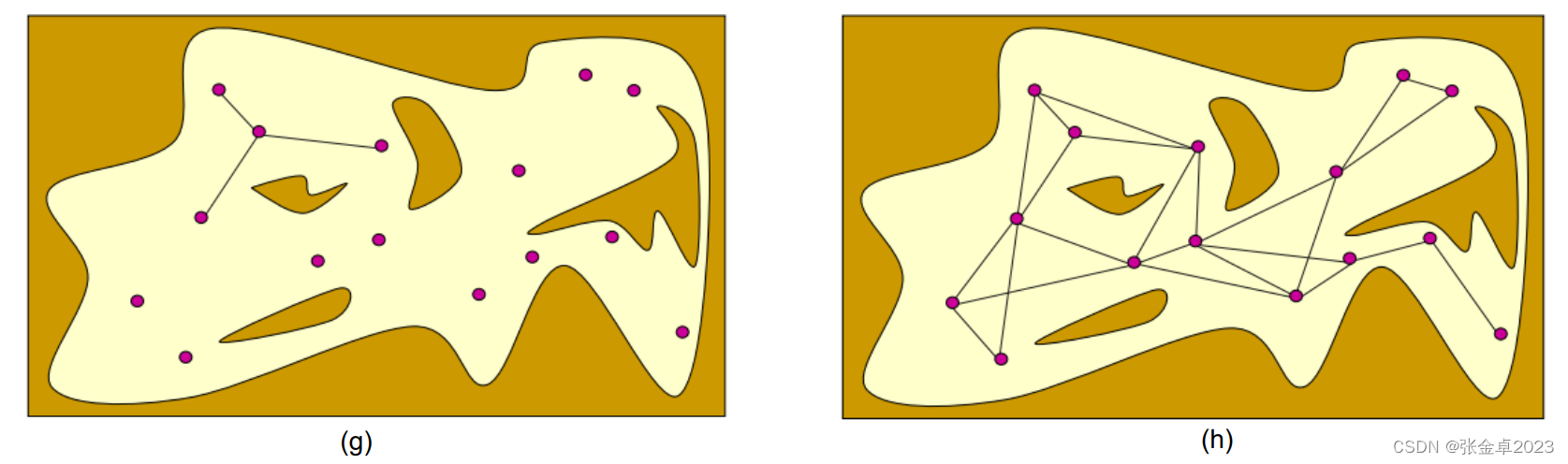（g）图中若采样点之间的连线与forbiden space相交则发生碰撞，删除发生碰撞的连线；
（f）图中碰撞检测通过的连线得到保留，作为构成图表graph的边；
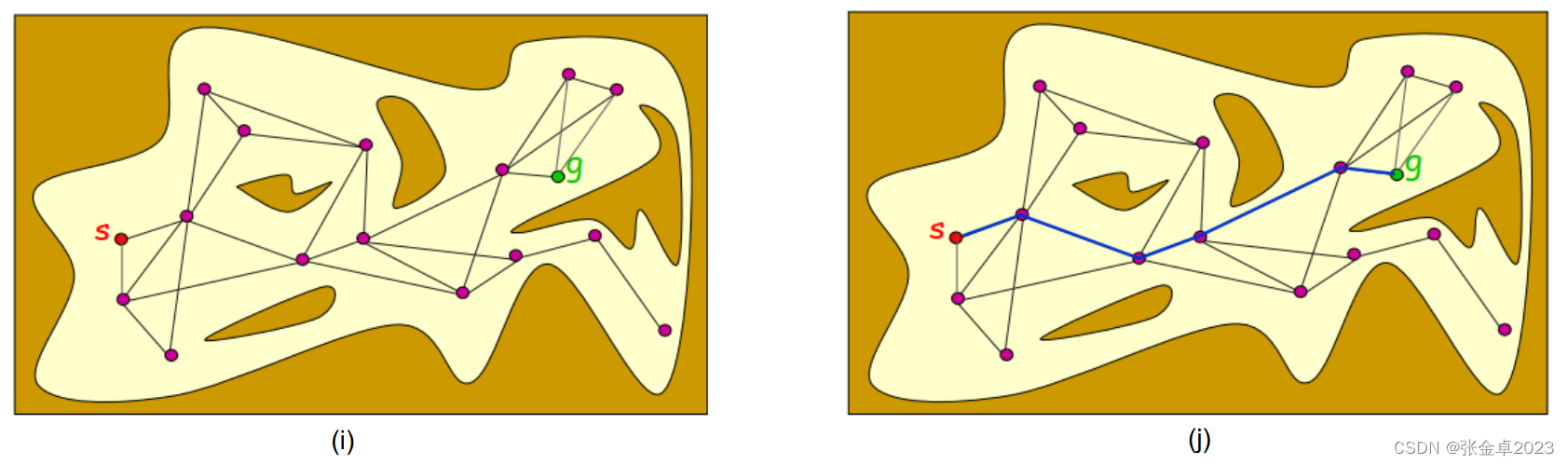
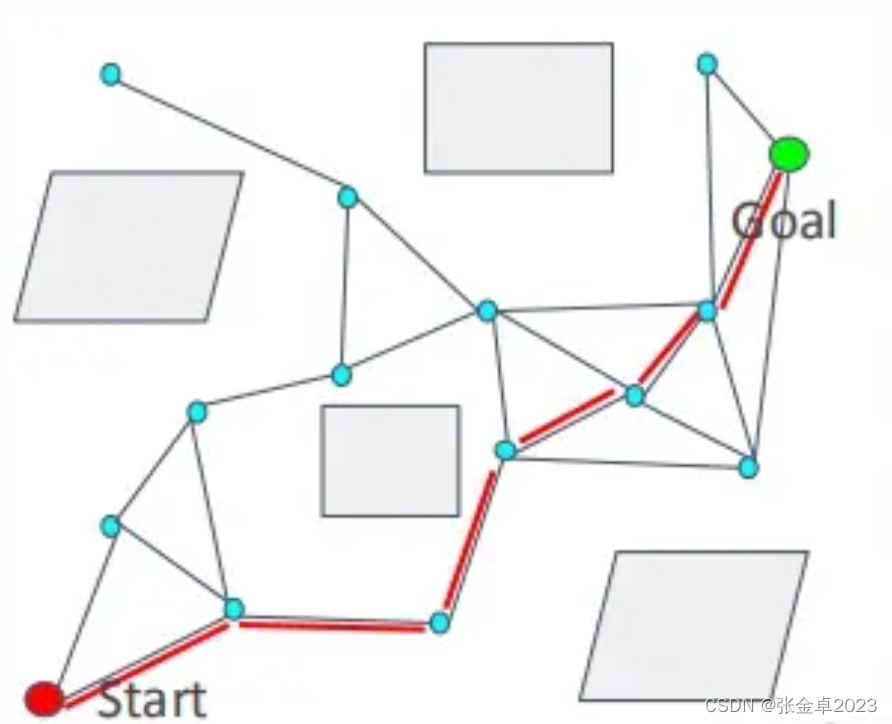
（i）在连线得到的图表graph中添加起始节点和目标节点；
（j）在graph图中利用图搜索算法寻找最优路径。
3、算法描述
用伪代码的方式对PRM进行简要描述：
V <- ∅; E <- ∅ // 分别维护两个集合，一个存放顶点，一个存放边
for i = 0,...,n do //假定最大采样点为n，进入循环x <- SampleFree; //在freespace通过特定的采样策略采样得到一个节点U <- Near(G = (V,E), x, r); //将节点半径r范围内要专注的邻居节点加入集合U中V <- V ∪ {x}; //将当前采样点x加入集合V中，更新集合Vforeach u in U, in order of increasing ||u - x||, do //对集合U中存入的节点进行处理，为了避免节点过于密集，u和x不能过于接近if x and u are not in the same connected component of G = (V,E) then // 保证u和x之间的连线与其他连线不重合if CollisionFree(x,u) then E <- E∪{(x,u),(u,x)}; // 通过碰撞检验则将x和u的连线加入集合E
return G=(V,E); // 返回V和E表示的图上面是经典的PRM算法描述，也可以对其进行简化：
V <- {x}∪{SampleFree}; E <- ∅;
foreach v in V do U <- near(G=(V,E),v,r)\{v};foreach u in U doif CollisionFree(v,u) then E <- E∪{(v,u),(u,v)}
return G=(V,E);主要就是减少了剔除部分节点的步骤，因此在算法实现上效率会降低。
4、节点连接处理
在PRM实现过程中，选择那些节点相连也是需要考虑的问题，下面给出三种可行的方法：
- k-Nearest PRM：选择当前节点最近的k个邻居节点
U ← kNearest(G=(V,E),v,k)
- Bounded-degree PRM：对半径范围内添加的最近节点添加一个边界值k
U ← Near(G,x,r) ∩ kNearest(G=(V,E),v,k)
- Variable-radius PRM：让连接半径称为对应节点个数的函数，而不是固定的参数
5、总结
PRM优点：具有概率完备性，只要采样点足够多，并且生成的图表有解那么一定可以结合图搜索算法找到一条最优解路径；
缺点：
- 如果是连接特定起点和终点，那么通过PRM的两个阶段先建图在搜索是比较浪费资源的；
- 搜索得到的路径是节点之间通过直线连接的，不符合车辆的运动学约束。
三、快速搜索随机树（RRT）
1、核心思想
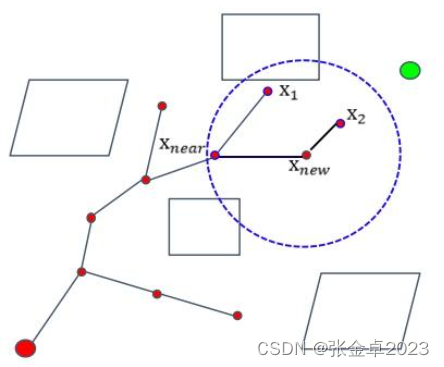
与PRM有学习和查询两个阶段，并且在学习阶段构造的是一个图不同，RRT只有一个阶段，在采样结束的同时就能确定路径，RRT在采样的过程中维护的是一个树结构。相比图描述的网络关系，树结构描述的是一种层次关系。
在RRT算法中，通常将起始节点作为树的根节点，在采样搜索到目标节点时通过回溯就可以确定路径。
2、实现流程
依然使用伪代码对实现流程进行简要描述：
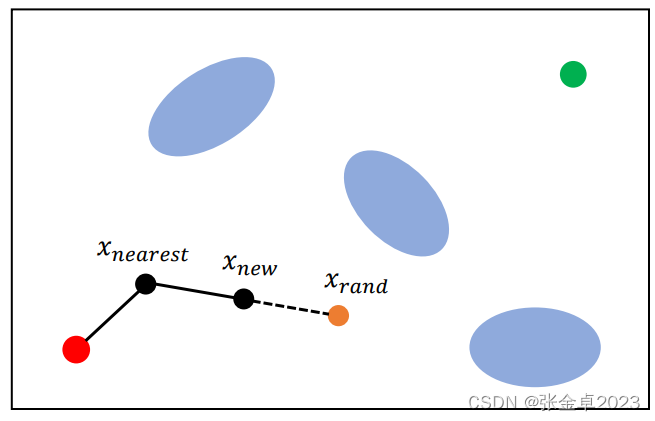
V <- {root}; E <- ∅; // 维护集合V和E,分别存放节点和边，在V中先将初始节点作为根节点放入
for i = 1,...,n doxrand ← SampleFree; // 在freespcace中得到采样点xrandxnearest ← Nearest(G=(V,E),xrand); // 设置离xrand距离最近的树节点为xnearestxnew ← steer(xnearest,xrand); // 通过特定的方式将xnearest与xrand进行连接，此处直接设置了一个中间节点，比较经典的方式设置一段弧长if ObtacleFree(xnearest,xrand) then // 进行连线障碍物检测V ← V∪{xnew}; E ← E∪{xnearest,xnew}; // 检测通过将边保存到集合E中
return G={V,E};
3、总结
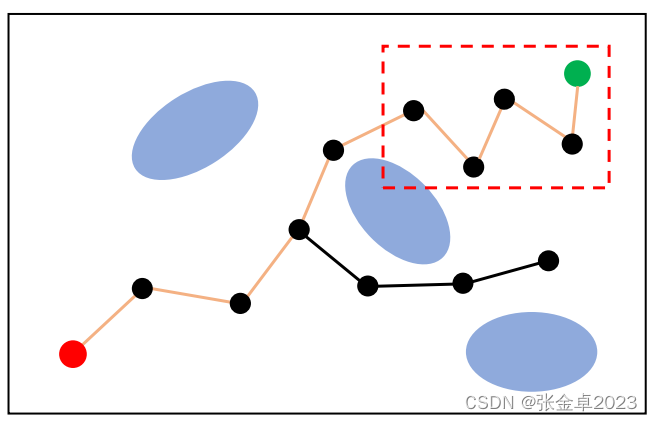
优点：如果是找寻找两个特定节点间的路径，RRT的效率会显著地优于PRM；
缺点：RRT不具备概率完备性，因为它每次都是树的最近节点连接，如下图红色区域中搜索得到的路径显然不是最优解。
4、改进RRT算法
为了解决RRT算法不具备概率完备性的缺陷，后来又提出了多种改进的RRT算法。
①快速搜索随机图（RRG）
V <- {root}; E <- ∅;
for i = 1,...,n doxrand ← SampleFree; xnearest ← Nearest(G=(V,E),xrand); xnew ← steer(xnearest,xrand);if ObtacleFree(xnearest,xrand) then Xnear ← Near(G=(V,E),xnew,min{γRRG(log(card(V))/card(V)^(1/d),η); // 将xnew附近给定半径内的所有节点都存入Xnear集合中V ← V∪{xnew}; E ← E∪{xnearest,xnew};foreach xnear in Xnear doif CollisionFree(xnear,xnew) then E ← E∪{xnearest,xnew}; // 将通过碰撞检测的所有Xnear集合中的节点与xnew的连线都存入集合E中return G={V,E};核心思想：不仅仅只是连接xnew和xnearest，将xnew半径范围内的所有符合非碰撞条件的节点都连接。
虽然RRG使得算法具有概率完备性，但是却违背了RRT算法提高效率的初衷，因为RRG算法在实现过程中并没有在维护树结构，输出的依然是一个图，相当于是PRM的学习阶段，还要再利用搜索算法进行最优路径确定。
②基于运动学的快速搜索随机树（Kinematic-based RRT）
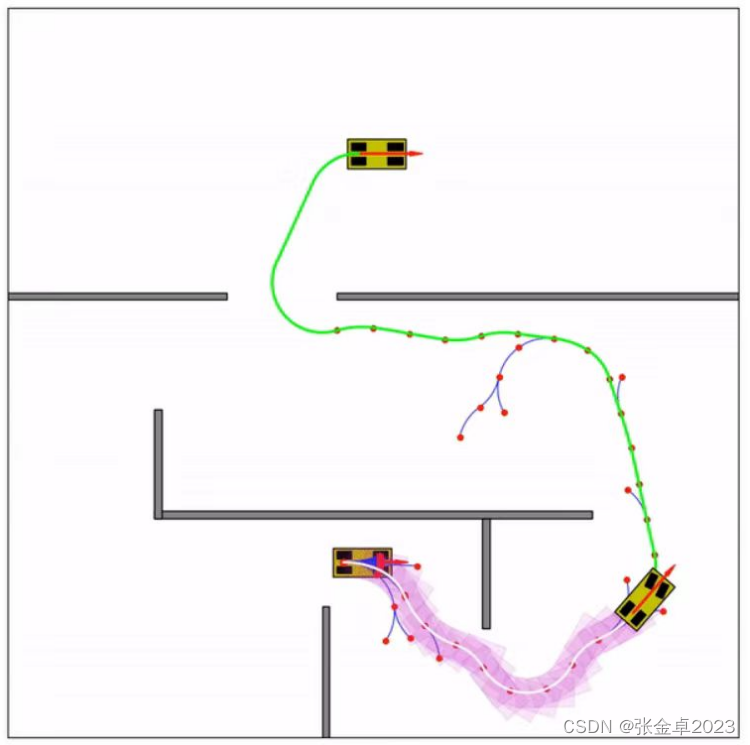
核心思想：利用车辆运动学方法在两个节点之间进行转向，主要在于RRT伪代码中xnew获取步骤的优化。
上图所示是基于杜宾斯规划（dubins_path_planning）得到的路径，可以看出在引入车辆运动学方法后，得到的最终路径是一条较为平滑的曲线。dubins_path_planning的具体介绍在后面会具体介绍。
四、优化的快速搜索随机数（RRT*）
1、核心思想
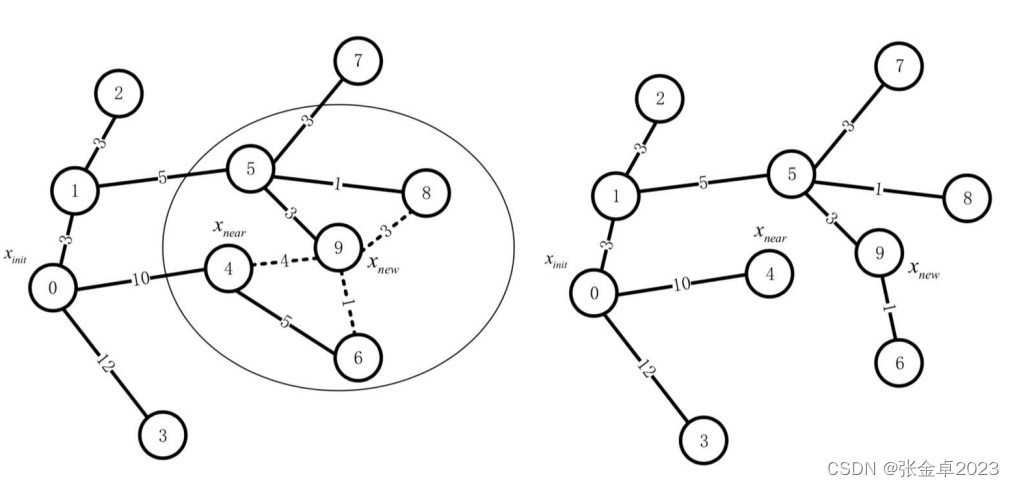
- 与RRG算法相比，RRT*算法维护的是一个树结构，而不是一个图，也就是说会在RRG得的图中删除掉多余的边界；
- 与原来的RRT算法相比，RRT*增加了重连的步骤以确保各个节点取得的是最小代价值。
2、实现流程
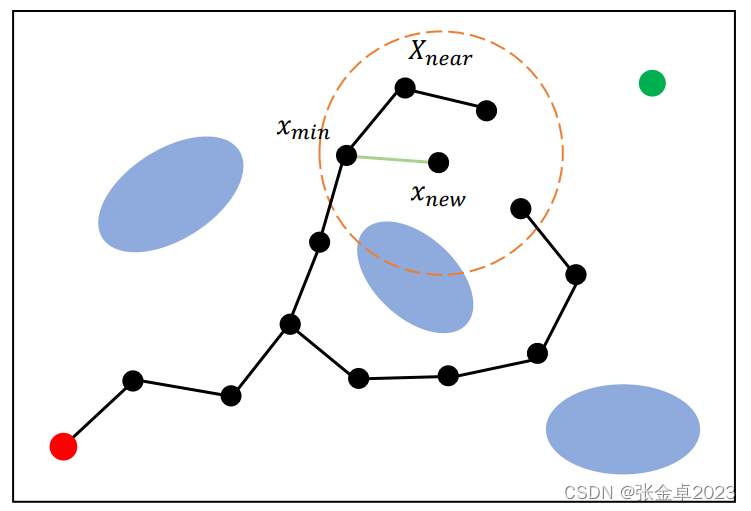
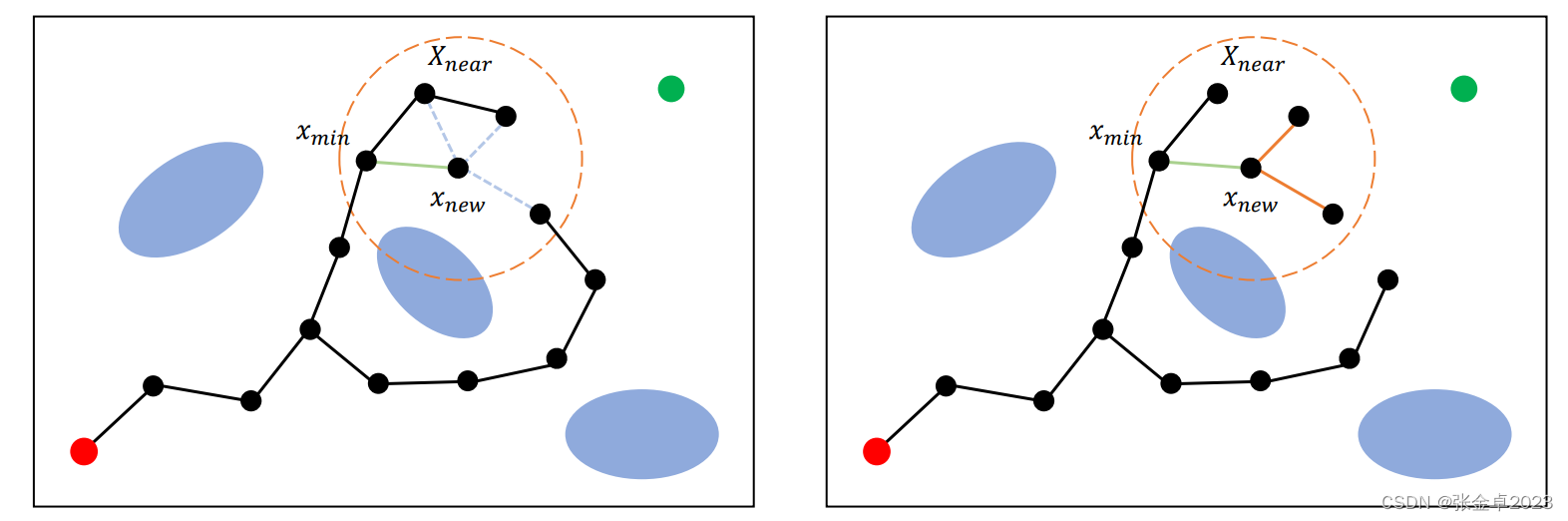
V <- {root}; E <- ∅;
for i = 1,...,n doxrand ← SampleFree; xnearest ← Nearest(G=(V,E),xrand); xnew ← steer(xnearest,xrand);if ObtacleFree(xnearest,xrand) then // 延续RRG的思想先搜索附近的邻居节点Xnear ← Near(G=(V,E),xnew,min{γRRG(log(card(V))/card(V)^(1/d),η); V ← V∪{xnew};xmin ← xnear; cmin ← Cost(xnearest) + c(Line(xnearest,xnew));// 获取代价值最小节点foreach xnear in Xnear do if CollisionFree(xnear,xnew) && Cost(xnew) + c(Line(xnearest,xnew)) < c(min) thenxmin ← xnear; cmin ← Cost(xnear) + c(Line(xnearest,xnew))// 对节点进行重连，通过xnew更新总代价值值和路径foreach xnear in Xnear do if CollisionFree(xnew,xnear) && Cost(xnew) + c(Line(xnew,xnearest)) < Cost(xnear)then xparent ← Parent(xnear);E ← (E\{xparent,xnear}∪{xnew,xnear}) // 在边集合中删除xnear到其原父节点xparent的连线，重新加入xnew到xnear的连线
return G = {V,E};
