java数据结构与算法刷题目录（剑指Offer、LeetCode、ACM）-----主目录-----持续更新(进不去说明我没写完)：https://blog.csdn.net/grd_java/article/details/123063846

1. 深度优先

解题思路：时间复杂度O($n^2$),空间复杂度O(n)

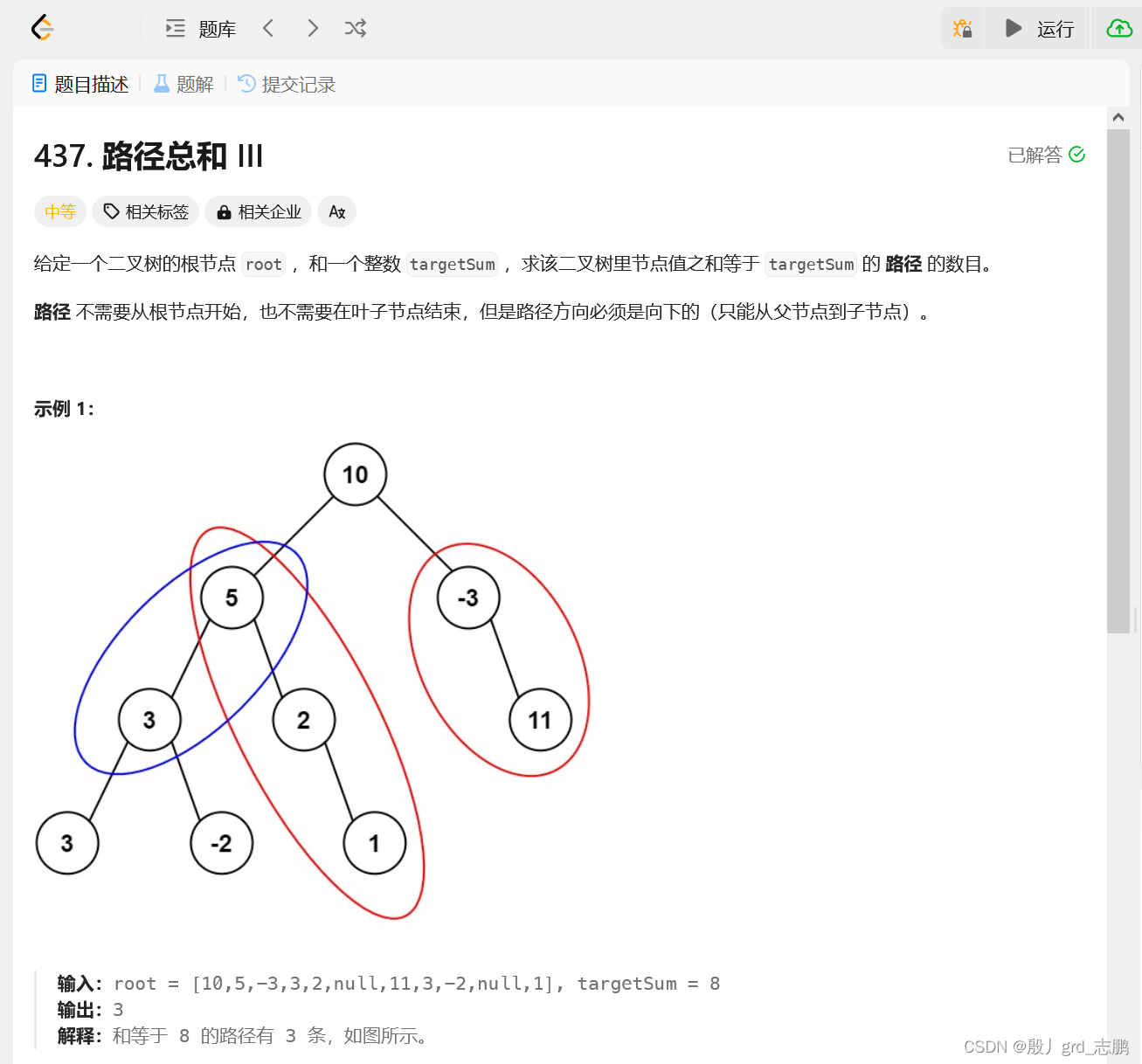
1. 从最下层结点开始，以每个结点为根结点，再次从上到下深度优先遍历
2. 试图找到符合条件的路径
3. 很显然，是双重深度优先遍历
4. 先深度优先遍历所有结点，然后每个结点还得再深度优先遍历一下找路径
5. 所以是N^2时间复杂度

代码

class Solution {//计算路径和public int pathSum(TreeNode root, int targetSum) {if (root == null) {return 0;}//获取以当前为根结点的路径和int ret = rootSum(root, targetSum);//深度优先遍历ret += pathSum(root.left, targetSum);ret += pathSum(root.right, targetSum);return ret;}//计算当前根结点的路径和，对于每个结点都进行从上到下的深度优先遍历//看看有没有符合条件的路径-------穷举法public int rootSum(TreeNode root, long targetSum) {int ret = 0;//深度优先，记录符合条件的路径数目if (root == null) {return 0;}int val = root.val;//获取当前结点值if (val == targetSum) {//如果当前值 == targetSum 结果+1，注意这里targetSum是减去前面结点，还需要多少ret++;} //深度优先，传入，targetSum - 当前结点值，还需要多少ret += rootSum(root.left, targetSum - val);//左子树符合条件的ret += rootSum(root.right, targetSum - val);//右子树符合条件的return ret;//返回当前结点符合条件的}
}

2. 前缀和

解题思路：时间复杂度O(n),空间复杂度O(n).其中空间复杂度是2n，因为需要一个map，深度优先遍历需要栈空间也是n，所以是2n时间复杂度，比上一个方法的空间复杂度多一倍。但是时间复杂度比它快n倍

1. 深度优先遍历
2. 遍历过程中，记录前缀和（就是从根结点到当前结点的和）到map中
3. 每遍历一个结点，都用当前前缀和 - 目标值，看看差多少，并从map中找这个差值

1. 如果找到这个差值，说明当前前缀 - 当前路径上的某个子前缀，是一个符合条件的路径
2. 如果没有，说明没找到，继续向下遍历

4. 当某个结点深度遍历完成，向上返回时，那么包含这个结点的前缀和就没有用了，需要从map中去掉

图解：找目标路径长度为8

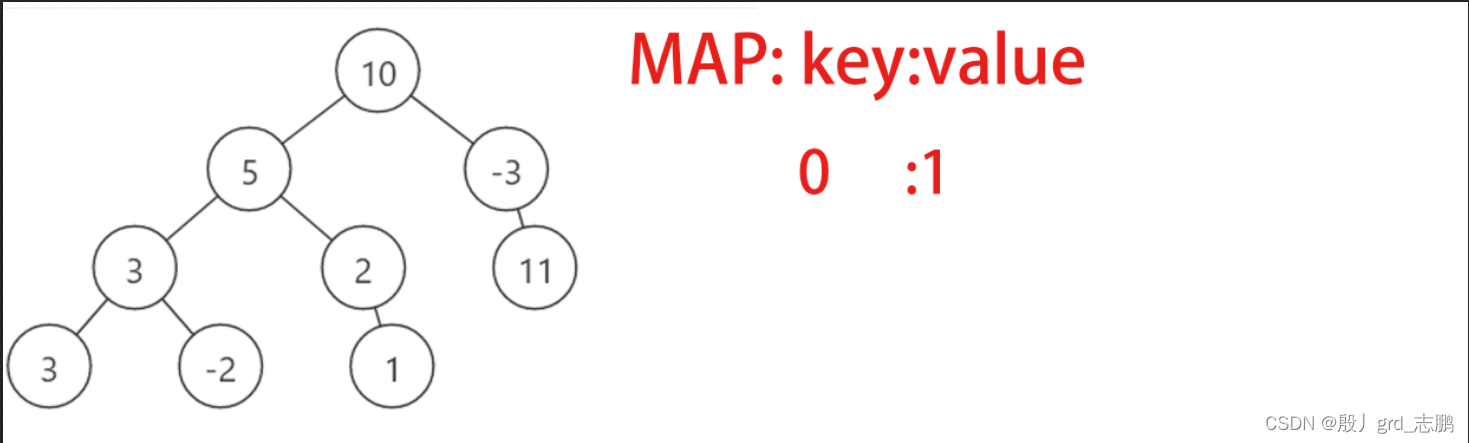
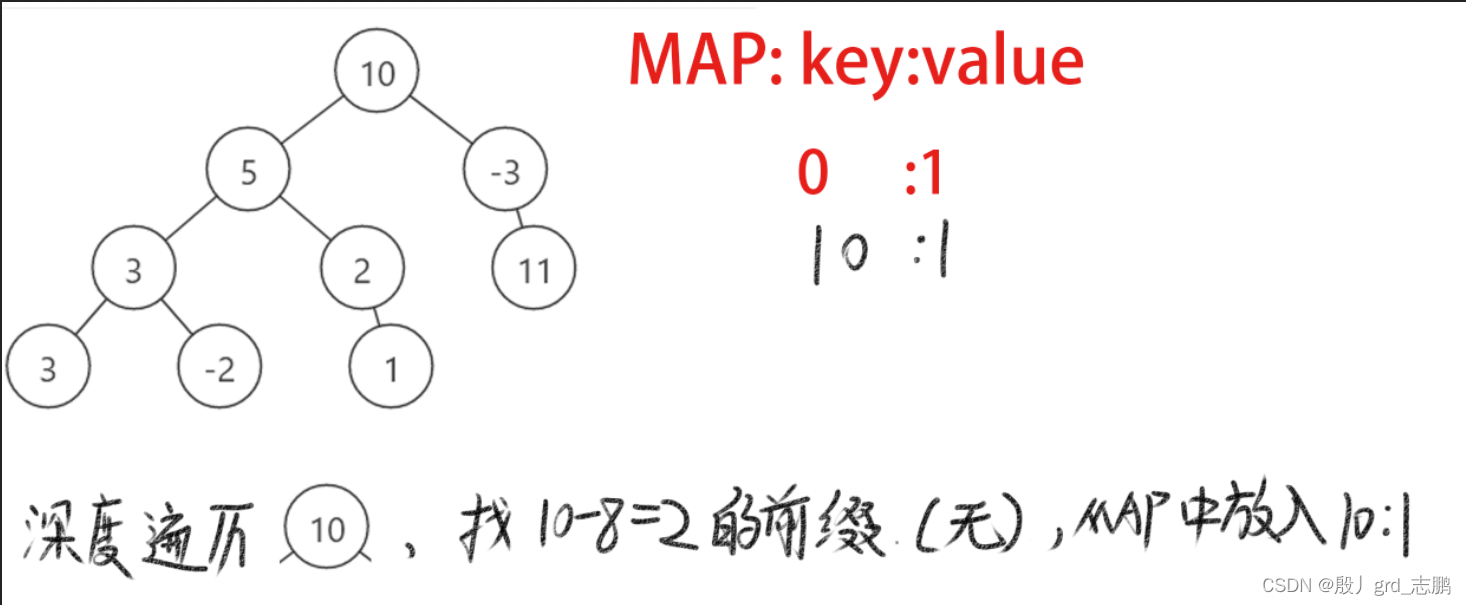
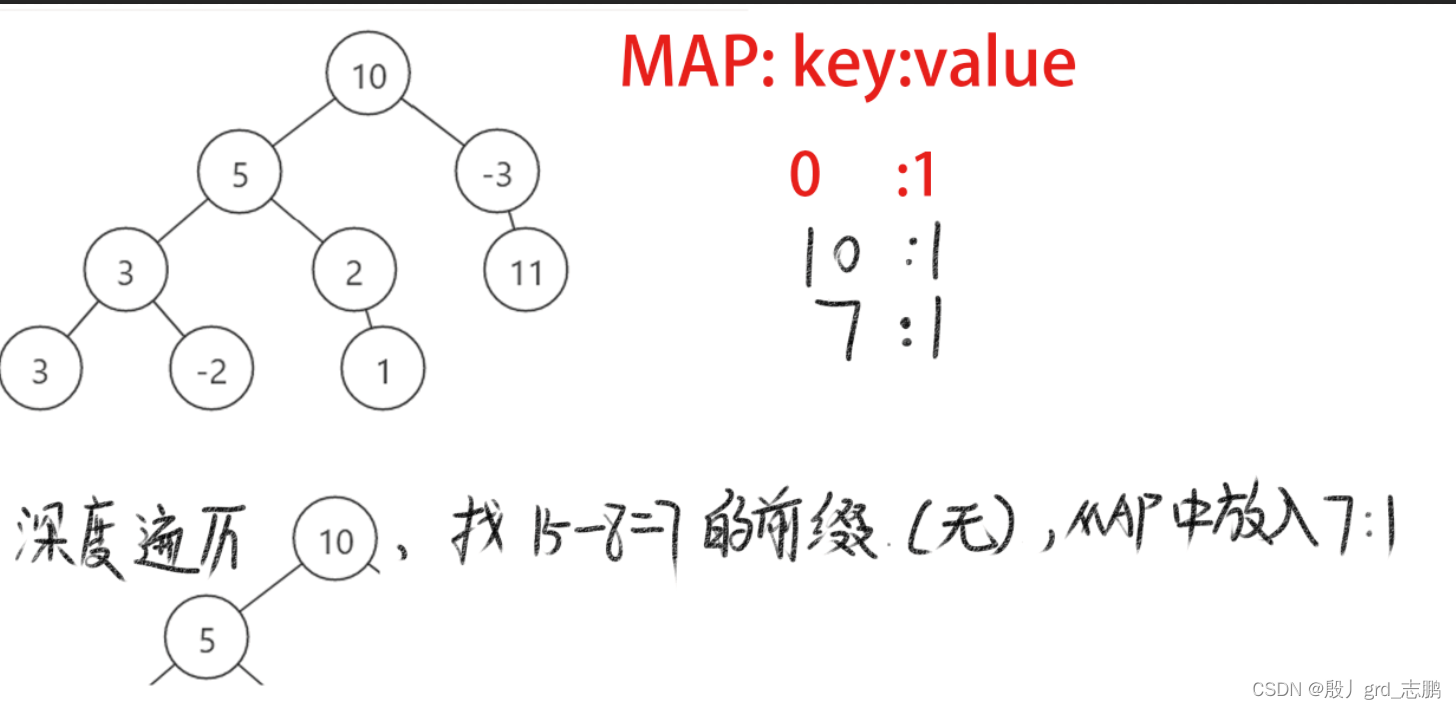
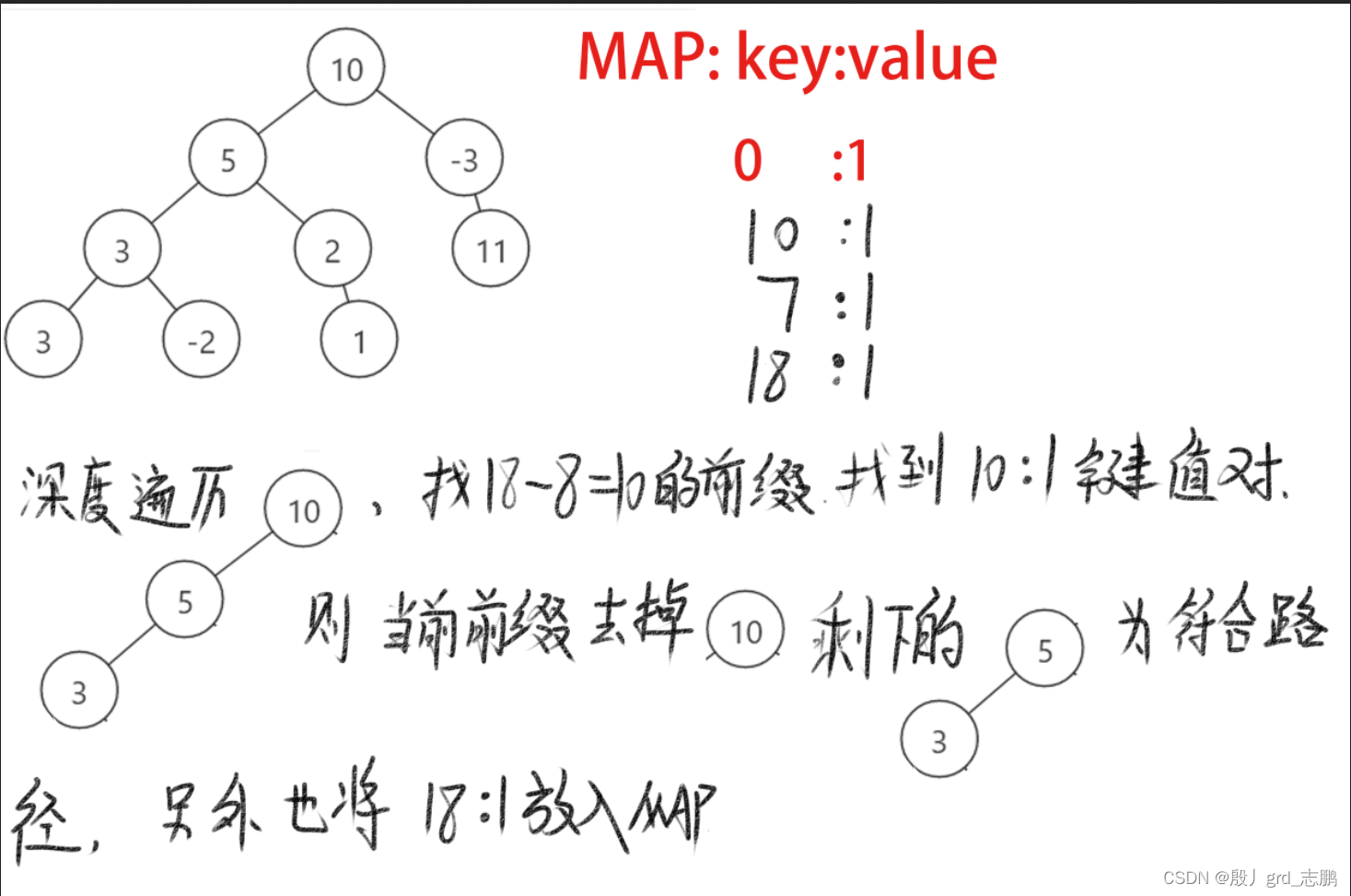
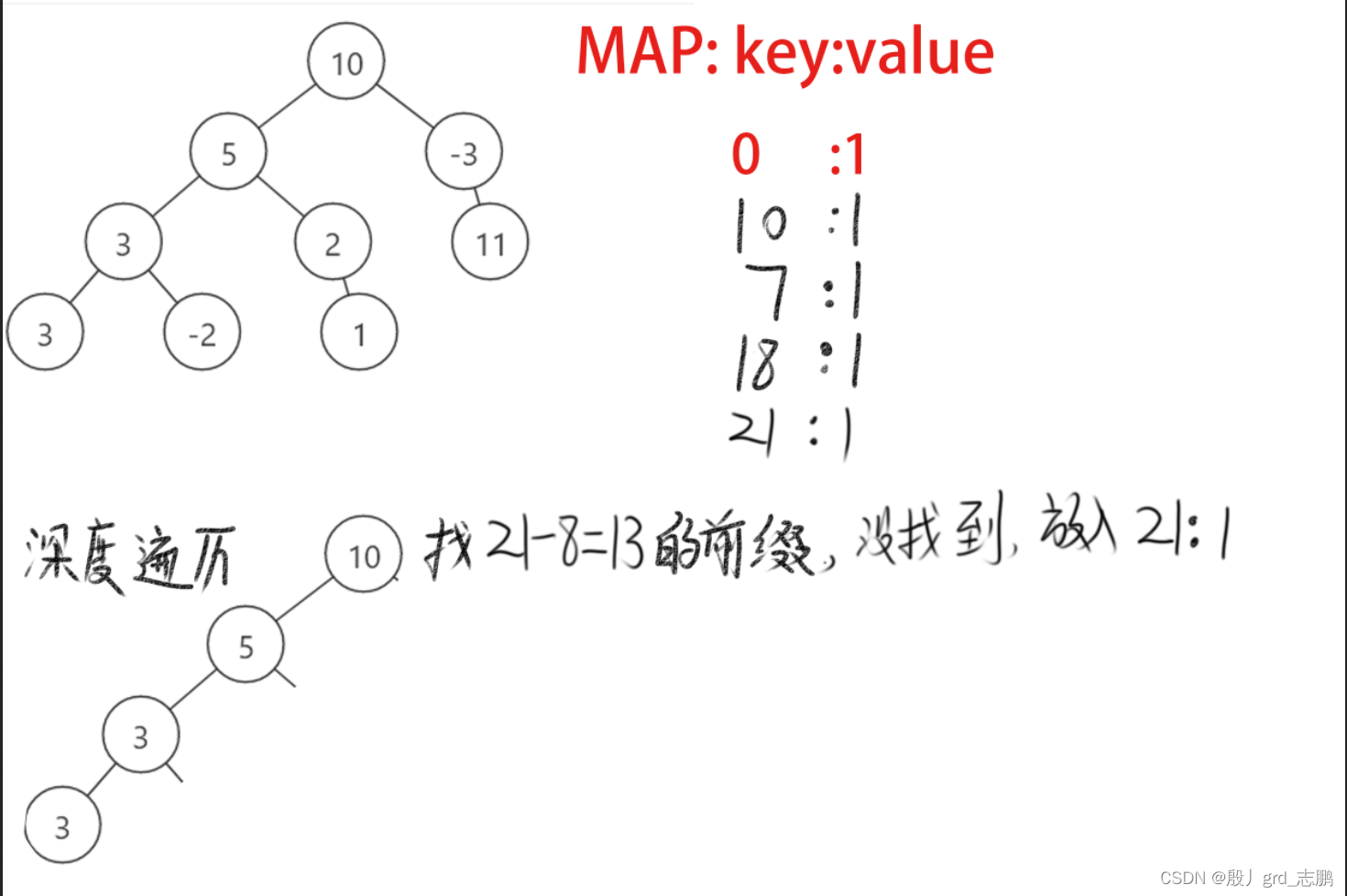
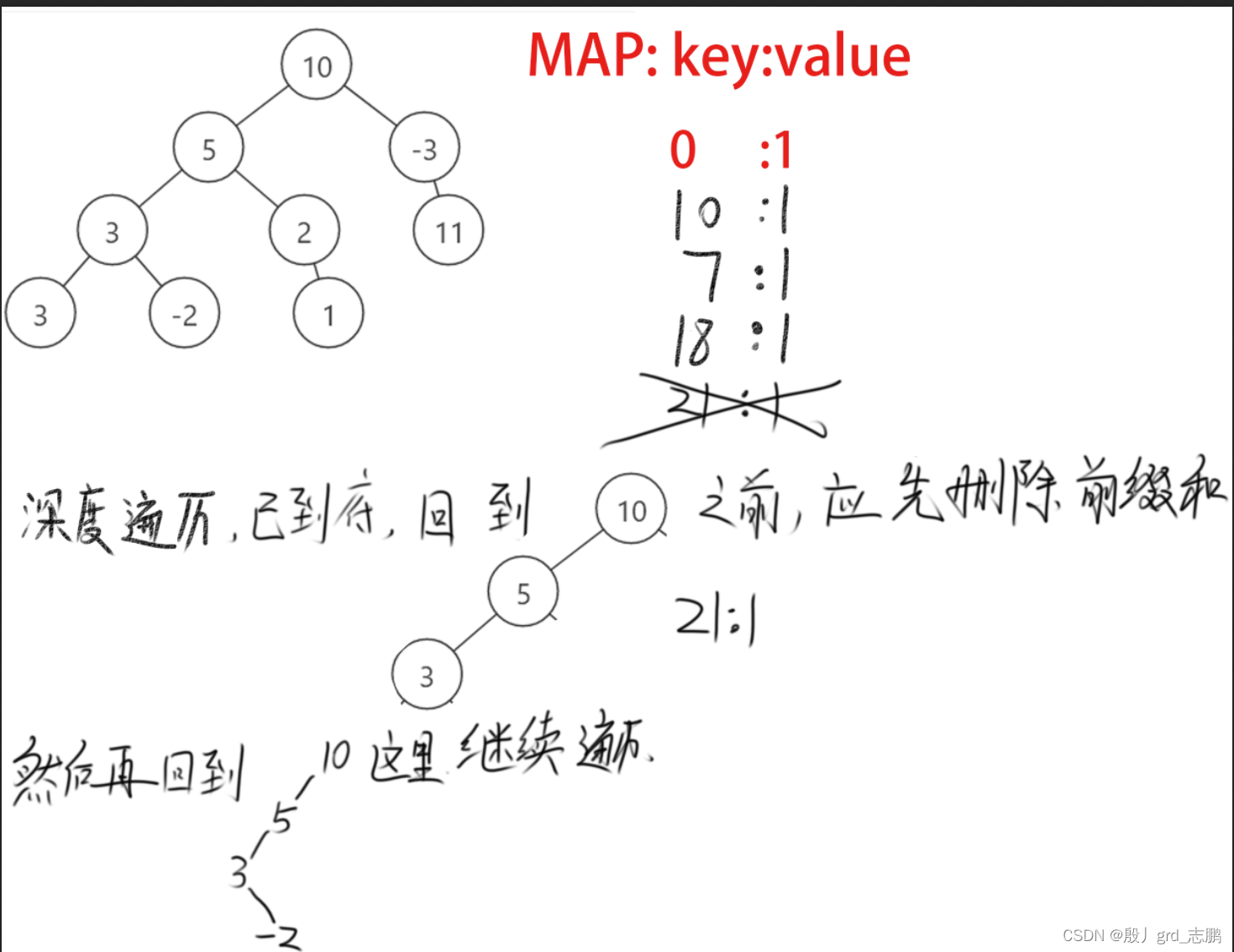
1. 初始状态下，前缀map，key保存前缀0，value保存此前缀有几个，为1
   
2. 深度遍历根结点10，则当前路径前缀长度为10，10 - 8 = 2，也就是当前前缀比目标值多2.不符合条件。继续深度优先遍历，并将当前前缀和10放入map，此前缀有目前有1个
   
3. 深度遍历到结点5，当前路径前缀和为15,15-8 = 7，map中找7找不到，所以将15:1放入map
   
4. 继续遍历到结点3，当前路径前缀和为18,18 - 8 = 10.此时map中发现10，也就是说，当前路径比目标值8多10，而10就在此路径的子前缀中，所以我们可以去掉10这个结点，这样我们就找到了第一个符合条件的路径，5和3。另外不要忘了将当前前缀和放入map，也就是18:1放入map
   
5. 继续向下，遍历结点3，此时发现前缀和为21,21 - 8 = 13，map中没有，放入前缀和21:1
   
6. 继续向下，我们发现已经到底，需要回溯了，回到父结点之前，需要先删除当前前缀和，21:1，然后再回父结点。之后继续遍历，重复上述步骤。
   

代码: 官方增加了测试用例，所以相同的代码已经无法击败100%了

class Solution {public int pathSum(TreeNode root, int targetSum) {Map<Long, Integer> prefix = new HashMap<Long, Integer>();//用Map保存前缀和prefix.put(0L, 1);//初始放入前缀和0，和其1return dfs(root, prefix, 0, targetSum);//进入递归}public int dfs(TreeNode root, Map<Long, Integer> prefix, long curr, int targetSum) {if (root == null) return 0;int ret = 0;//符合条件的路径条数curr += root.val;//当前路径值（前缀和）//看看当前路径和 - 目标值，是否等于路径上的一个前缀//如果是的话，说明当前路径，去掉某些前缀结点，刚好符合targetSum//如果没有，那么ret依然是0ret = prefix.getOrDefault(curr - targetSum, 0);//将当前路径前缀和，加入到map中prefix.put(curr, prefix.getOrDefault(curr, 0) + 1);//深度优先ret += dfs(root.left, prefix, curr, targetSum);ret += dfs(root.right, prefix, curr, targetSum);//----------当此结点的遍历出栈时，要将map中对应的前缀和去掉。否则其它路径的前缀和很可能和当前路径的前缀和冲突-------------prefix.put(curr, prefix.getOrDefault(curr, 0) - 1);//返回符合条件路径条数return ret;}
}