LeetCode 每日一题树合集 Day 16

终于是开学了，想了想每日一更频率太高，以后每周更新一周的每日一题。

103. 二叉树的锯齿形层序遍历

给你二叉树的根节点 root ，返回其节点值的锯齿形层序遍历。（即先从左往右，再从右往左进行下一层遍历，以此类推，层与层之间交替进行）。

示例 1：

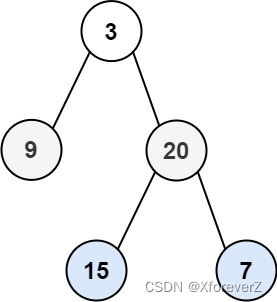
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[20,9],[15,7]]
示例 2：

输入：root = [1]
输出：[[1]]
示例 3：

输入：root = []
输出：[]

提示：

树中节点数目在范围 [0, 2000] 内
-100 <= Node.val <= 100

广度优先遍历（BFS）:

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:vector<vector<int>> zigzagLevelOrder(TreeNode* root) {if (!root) {return {};}vector<TreeNode*> temp, lists;lists.push_back(root);bool isLeft = true;vector<vector<int>> res;vector<int> tt;while (!lists.empty()) {tt.clear();temp.clear();for (auto it : lists) {tt.push_back(it->val);if (it->left) {temp.push_back(it->left);}if (it->right) {temp.push_back(it->right);}}lists = temp;if (!isLeft) {reverse(tt.begin(), tt.end());}isLeft = !isLeft;res.push_back(tt);}return res;}
};

429. N 叉树的层序遍历

给定一个 N 叉树，返回其节点值的层序遍历。（即从左到右，逐层遍历）。

树的序列化输入是用层序遍历，每组子节点都由 null 值分隔（参见示例）。

示例 1：

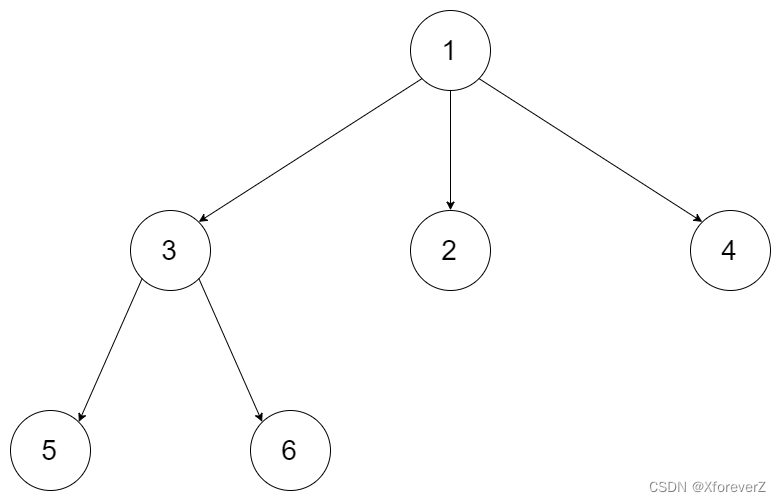
输入：root = [1,null,3,2,4,null,5,6]
输出：[[1],[3,2,4],[5,6]]
示例 2：

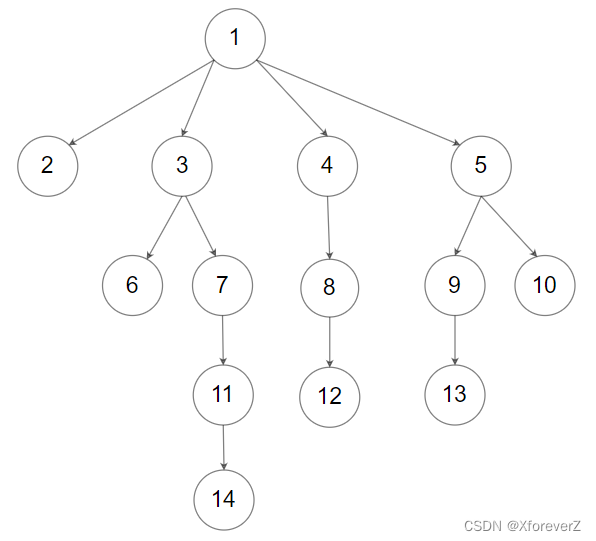
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[[1],[2,3,4,5],[6,7,8,9,10],[11,12,13],[14]]

提示：

树的高度不会超过 1000
树的节点总数在 [0, 10^4] 之间

树的层序遍历，代码随想录的卡哥总结的很好，读者有兴趣可以看看：「代码随想录」二叉树层序遍历登场：我要打十个！

/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/
class Solution {
public:vector<vector<int>> levelOrder(Node* root) {queue<Node*> que;vector<vector<int>> result;if (root != NULL)que.push(root);while (!que.empty()) {int size = que.size();vector<int> vec;for (int i = 0; i < size; i++) {Node* node = que.front();que.pop();vec.push_back(node->val);for (int i = 0; i < node->children.size(); i++) {if (node->children[i]) {que.push(node->children[i]);}}}result.push_back(vec);}return result;}
};

589. N 叉树的前序遍历

给定一个 n 叉树的根节点 root ，返回其节点值的前序遍历。

n 叉树在输入中按层序遍历进行序列化表示，每组子节点由空值 null 分隔（请参见示例）。

示例 1：

输入：root = [1,null,3,2,4,null,5,6]
输出：[1,3,5,6,2,4]
示例 2：

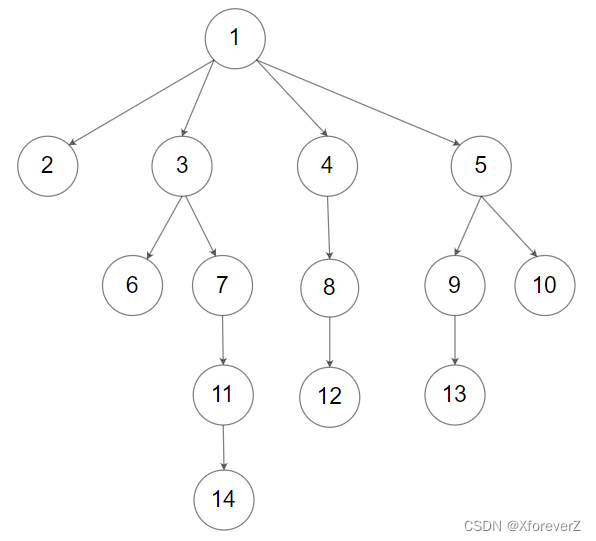
输入：root = [1,null,2,3,4,5,null,null,6,7,null,8,null,9,10,null,null,11,null,12,null,13,null,null,14]
输出：[1,2,3,6,7,11,14,4,8,12,5,9,13,10]

提示：

节点总数在范围 [0, 104]内
0 <= Node.val <= 1e4
n 叉树的高度小于或等于 1000

进阶：递归法很简单，你可以使用迭代法完成此题吗?

同样的前中后序递归与非递归的方法卡哥也有所总结，对于求职的基础知识掌握很有帮助:
「代码随想录」彻底吃透前中后序递归法（递归三部曲）和迭代法

/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution {
private:vector<int> res;void traversal(Node* root) {if (root == NULL) {return;}res.push_back(root->val);for (int i = 0; i < root->children.size(); i++) {traversal(root->children[i]);}}public:vector<int> preorder(Node* root) {res.clear();traversal(root);return res;}
};

590. N 叉树的后序遍历

/*
// Definition for a Node.
class Node {
public:int val;vector<Node*> children;Node() {}Node(int _val) {val = _val;}Node(int _val, vector<Node*> _children) {val = _val;children = _children;}
};
*/class Solution {
private:vector<int> res;void traversal(Node* root) {if (root == NULL) {return;}for (int i = 0; i < root->children.size(); i++) {traversal(root->children[i]);}res.push_back(root->val);}public:vector<int> postorder(Node* root) {res.clear();traversal(root);return res;}
};

105. 从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例 1:

输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
示例 2:

输入: preorder = [-1], inorder = [-1]
输出: [-1]

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均无重复元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

二叉树基础，同样的代码随想录里面也总结的很好：「代码随想录」带你学透二叉树！【中序和后序&&中序和前序】构造二叉树

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
private:vector<int> preorder;unordered_map<int, int> dic;TreeNode* recur(int root, int left, int right) {if (left > right)return nullptr;TreeNode* node = new TreeNode(preorder[root]);int i = dic[preorder[root]];node->left = recur(root + 1, left, i - 1);node->right = recur(root + i - left + 1, i + 1, right);return node;}public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {this->preorder = preorder;for (int i = 0; i < inorder.size(); i++)dic[inorder[i]] = i;return recur(0, 0, inorder.size() - 1);}
};

106. 从中序与后序遍历序列构造二叉树

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗二叉树。

示例 1:

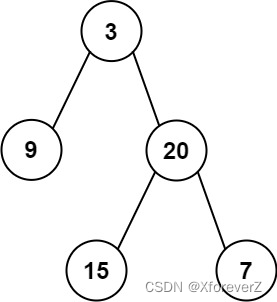
输入：inorder = [9,3,15,20,7], postorder = [9,15,7,20,3]
输出：[3,9,20,null,null,15,7]
示例 2:

输入：inorder = [-1], postorder = [-1]
输出：[-1]

提示:

1 <= inorder.length <= 3000
postorder.length == inorder.length
-3000 <= inorder[i], postorder[i] <= 3000
inorder 和 postorder 都由不同的值组成
postorder 中每一个值都在 inorder 中
inorder 保证是树的中序遍历
postorder 保证是树的后序遍历

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:unordered_map<int, int> pos;TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {int n = inorder.size();for (int i = 0; i < n; i++) {pos[inorder[i]] = i;}return dfs(inorder, postorder, 0, n - 1, 0, n - 1);}TreeNode* dfs(vector<int>& inorder, vector<int>& postorder, int il, int ir,int pl, int pr) {if (il > ir)return nullptr;int k = pos[postorder[pr]];TreeNode* root = new TreeNode(postorder[pr]);root->left = dfs(inorder, postorder, il, k - 1, pl, pl + k - 1 - il);root->right =dfs(inorder, postorder, k + 1, ir, pl + k - 1 - il + 1, pr - 1);return root;}
};

889. 根据前序和后序遍历构造二叉树

给定两个整数数组，preorder 和 postorder ，其中 preorder 是一个具有无重复值的二叉树的前序遍历，postorder 是同一棵树的后序遍历，重构并返回二叉树。

如果存在多个答案，您可以返回其中任何一个。

示例 1：

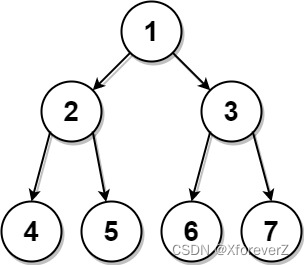
输入：preorder = [1,2,4,5,3,6,7], postorder = [4,5,2,6,7,3,1]
输出：[1,2,3,4,5,6,7]
示例 2:

输入: preorder = [1], postorder = [1]
输出: [1]

提示：

1 <= preorder.length <= 30
1 <= preorder[i] <= preorder.length
preorder 中所有值都不同
postorder.length == preorder.length
1 <= postorder[i] <= postorder.length
postorder 中所有值都不同
保证 preorder 和 postorder 是同一棵二叉树的前序遍历和后序遍历

只知道前序和后序构造的二叉树是不唯一的
这里我觉得灵神的题解很清晰：【图解】从 O(n^2) 到 O(n)

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:TreeNode* constructFromPrePost(vector<int>& preorder,vector<int>& postorder) {if (preorder.empty()) {return nullptr;}if (preorder.size() == 1) {return new TreeNode(preorder[0]);}int left_size =ranges::find(postorder, preorder[1]) - postorder.begin() + 1;vector<int> pre1(preorder.begin() + 1,preorder.begin() + 1 + left_size);vector<int> pre2(preorder.begin() + 1 + left_size, preorder.end());vector<int> post1(postorder.begin(), postorder.begin() + left_size);vector<int> post2(postorder.begin() + left_size, postorder.end() - 1);TreeNode* left = constructFromPrePost(pre1, post1);TreeNode* right = constructFromPrePost(pre2, post2);return new TreeNode(preorder[0], left, right);}
};

2583. 二叉树中的第 K 大层和

给你一棵二叉树的根节点 root 和一个正整数 k 。

树中的层和是指同一层上节点值的总和。

返回树中第 k 大的层和（不一定不同）。如果树少于 k 层，则返回 -1 。

注意，如果两个节点与根节点的距离相同，则认为它们在同一层。

示例 1：

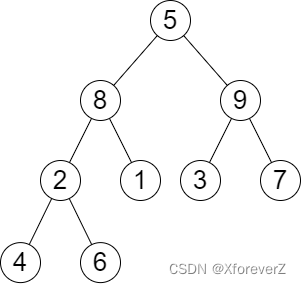
输入：root = [5,8,9,2,1,3,7,4,6], k = 2
输出：13
解释：树中每一层的层和分别是：

Level 1: 5
Level 2: 8 + 9 = 17
Level 3: 2 + 1 + 3 + 7 = 13
Level 4: 4 + 6 = 10
第 2 大的层和等于 13 。
示例 2：

输入：root = [1,2,null,3], k = 1
输出：3
解释：最大的层和是 3 。

提示：

树中的节点数为 n
2 <= n <= 105
1 <= Node.val <= 106
1 <= k <= n

BFS+排序：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:long long kthLargestLevelSum(TreeNode* root, int k) {vector<long long> arr;queue<TreeNode*> q{{root}};while (!q.empty()) {long long t = 0;for (int n = q.size(); n; --n) {root = q.front();q.pop();t += root->val;if (root->left) {q.push(root->left);}if (root->right) {q.push(root->right);}}arr.push_back(t);}if (arr.size() < k) {return -1;}sort(arr.rbegin(), arr.rend());return arr[k - 1];}
};

2476. 二叉搜索树最近节点查询

给你一个二叉搜索树的根节点 root ，和一个由正整数组成、长度为 n 的数组 queries 。

请你找出一个长度为 n 的二维答案数组 answer ，其中 answer[i] = [mini, maxi] ：

mini 是树中小于等于 queries[i] 的最大值。如果不存在这样的值，则使用 -1 代替。
maxi 是树中大于等于 queries[i] 的最小值。如果不存在这样的值，则使用 -1 代替。
返回数组 answer 。

示例 1 ：

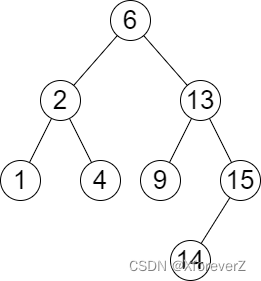
输入：root = [6,2,13,1,4,9,15,null,null,null,null,null,null,14], queries = [2,5,16]
输出：[[2,2],[4,6],[15,-1]]
解释：按下面的描述找出并返回查询的答案：

树中小于等于 2 的最大值是 2 ，且大于等于 2 的最小值也是 2 。所以第一个查询的答案是 [2,2] 。
树中小于等于 5 的最大值是 4 ，且大于等于 5 的最小值是 6 。所以第二个查询的答案是 [4,6] 。
树中小于等于 16 的最大值是 15 ，且大于等于 16 的最小值不存在。所以第三个查询的答案是 [15,-1] 。
示例 2 ：

输入：root = [4,null,9], queries = [3]
输出：[[-1,4]]
解释：树中不存在小于等于 3 的最大值，且大于等于 3 的最小值是 4 。所以查询的答案是 [-1,4] 。

提示：

树中节点的数目在范围 [2, 1e5] 内
1 <= Node.val <= 1e6
n == queries.length
1 <= n <= 105
1 <= queries[i] <= 1e6

中序遍历 + 二分：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {vector<int> a;void dfs(TreeNode* node) {if (node == nullptr) {return;}dfs(node->left);a.push_back(node->val);dfs(node->right);};public:vector<vector<int>> closestNodes(TreeNode* root, vector<int>& queries) {dfs(root);int n = a.size();vector<vector<int>> ans;for (int q : queries) {int j = ranges::lower_bound(a, q) - a.begin();int mx = j < n ? a[j] : -1;if (j == n || a[j] != q) {j--;}int mn = j >= 0 ? a[j] : -1;ans.push_back({mn, mx});}return ans;}
};

菜鸡抄的题解（orz

235. 二叉搜索树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

例如，给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]

示例 1:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
示例 2:

输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
输出: 2
解释: 节点 2 和节点 4 的最近公共祖先是 2, 因为根据定义最近公共祖先节点可以为节点本身。

说明:

所有节点的值都是唯一的。
p、q 为不同节点且均存在于给定的二叉搜索树中。

递归：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode(int x) : val(x), left(NULL), right(NULL) {}* };*/class Solution {
public:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {int x = root->val;if (p->val < x && q->val < x)return lowestCommonAncestor(root->left, p, q);if (p->val > x and q->val > x)return lowestCommonAncestor(root->right, p, q);return root;}
};

938. 二叉搜索树的范围和

给定二叉搜索树的根结点 root，返回值位于范围 [low, high] 之间的所有结点的值的和。

示例 1：

输入：root = [10,5,15,3,7,null,18], low = 7, high = 15
输出：32
示例 2：

输入：root = [10,5,15,3,7,13,18,1,null,6], low = 6, high = 10
输出：23

提示：

树中节点数目在范围 [1, 2 * 104] 内
1 <= Node.val <= 105
1 <= low <= high <= 105
所有 Node.val 互不相同

递归：

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),* right(right) {}* };*/
class Solution {
public:int rangeSumBST(TreeNode* root, int low, int high) {if (root == nullptr) {return 0;}int x = root->val;if (x > high) {return rangeSumBST(root->left, low, high);}if (x < low) {return rangeSumBST(root->right, low, high);}return x + rangeSumBST(root->left, low, high) + rangeSumBST(root->right, low, high);}
};

2867. 统计树中的合法路径数目(Hard)

给你一棵 n 个节点的无向树，节点编号为 1 到 n 。给你一个整数 n 和一个长度为 n - 1 的二维整数数组 edges ，其中 edges[i] = [ui, vi] 表示节点 ui 和 vi 在树中有一条边。

请你返回树中的合法路径数目。

如果在节点 a 到节点 b 之间恰好有一个节点的编号是质数，那么我们称路径 (a, b) 是合法的。

注意：

路径 (a, b) 指的是一条从节点 a 开始到节点 b 结束的一个节点序列，序列中的节点互不相同，且相邻节点之间在树上有一条边。
路径 (a, b) 和路径 (b, a) 视为同一条路径，且只计入答案一次。

示例 1：

输入：n = 5, edges = [[1,2],[1,3],[2,4],[2,5]]
输出：4
解释：恰好有一个质数编号的节点路径有：

(1, 2) 因为路径 1 到 2 只包含一个质数 2 。
(1, 3) 因为路径 1 到 3 只包含一个质数 3 。
(1, 4) 因为路径 1 到 4 只包含一个质数 2 。
(2, 4) 因为路径 2 到 4 只包含一个质数 2 。
只有 4 条合法路径。
示例 2：

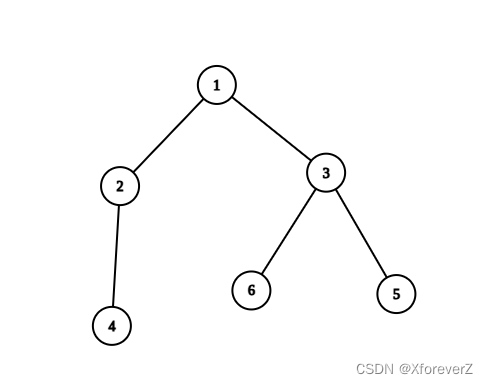
输入：n = 6, edges = [[1,2],[1,3],[2,4],[3,5],[3,6]]
输出：6
解释：恰好有一个质数编号的节点路径有：

(1, 2) 因为路径 1 到 2 只包含一个质数 2 。
(1, 3) 因为路径 1 到 3 只包含一个质数 3 。
(1, 4) 因为路径 1 到 4 只包含一个质数 2 。
(1, 6) 因为路径 1 到 6 只包含一个质数 3 。
(2, 4) 因为路径 2 到 4 只包含一个质数 2 。
(3, 6) 因为路径 3 到 6 只包含一个质数 3 。
只有 6 条合法路径。

提示：

1 <= n <= 1e5
edges.length == n - 1
edges[i].length == 2
1 <= ui, vi <= n
输入保证 edges 形成一棵合法的树。

看了题解：【图解】O(n) 线性做法

const int MX = 1e5;
bool np[MX + 1]; // 质数=false 非质数=true
int init = []() {np[1] = true;for (int i = 2; i * i <= MX; i++) {if (!np[i]) {for (int j = i * i; j <= MX; j += i) {np[j] = true;}}}return 0;
}();class Solution {
public:long long countPaths(int n, vector<vector<int>>& edges) {vector<vector<int>> g(n + 1);for (auto& e : edges) {int x = e[0], y = e[1];g[x].push_back(y);g[y].push_back(x);}vector<int> size(n + 1);vector<int> nodes;function<void(int, int)> dfs = [&](int x, int fa) {nodes.push_back(x);for (int y : g[x]) {if (y != fa && np[y]) {dfs(y, x);}}};long long ans = 0;for (int x = 1; x <= n; x++) {if (np[x])continue; // 跳过非质数int sum = 0;for (int y : g[x]) { // 质数 x 把这棵树分成了若干个连通块if (!np[y])continue;if (size[y] == 0) { // 尚未计算过nodes.clear();dfs(y,-1); // 遍历 y// 所在连通块，在不经过质数的前提下，统计有多少个非质数for (int z : nodes) {size[z] = nodes.size();}}// 这 size[y] 个非质数与之前遍历到的 sum// 个非质数，两两之间的路径只包含质数 xans += (long long)size[y] * sum;sum += size[y];}ans += sum; // 从 x 出发的路径}return ans;}
};

BFS 解法也是可以的：

class Solution {
public:long long countPaths(int n, vector<vector<int>>& edges) {vector<vector<int>> adj(n + 1);for (vector<int> e : edges) {adj[e[0]].emplace_back(e[1]);adj[e[1]].emplace_back(e[0]);}bool prime[n + 1];memset(prime, true, sizeof(prime));bool visited[n + 1];memset(visited, false, sizeof(visited));function<void(int)> SieveOfEratosthenes = [&](int val) {for (int p = 2; p * p <= n; p++) {if (prime[p] == true) {for (int i = p * p; i <= n; i += p)prime[i] = false;}}};SieveOfEratosthenes(n);prime[1] = false;map<int, vector<int>> rec;map<int, long long> group;visited[1] = true;long long res = 0;function<void(int)> traverse = [&](int cur) {if (prime[cur]) {for (int a : adj[cur]) {if (!visited[a]) {visited[a] = true;traverse(a);}}}else {if (group[cur] != 0)return;queue<int> bfs;int size = 0;visited[cur] = true;bfs.push(cur);while (!bfs.empty()) {int l = bfs.size();for (int i = 0; i < l; ++i) {int t = bfs.front();bfs.pop();size++;for (int a : adj[t]) {if (prime[a]) {rec[cur].emplace_back(a);if (!visited[a]) {visited[a] = true;traverse(a);}} else {if (!visited[a]) {visited[a] = true;bfs.push(a);}}}}}group[cur] = size;for (int nei : rec[cur]) {res += group[nei] * size;res += size;group[nei] += size;}}};traverse(1);return res;}
};