MATLAB环境下脑电信号EEG的谱分析

脑电信号一直伴随着人类的生命，脑电波是脑神经细胞发生新陈代谢、离子交换时细胞群兴奋突触电位总和，脑电信号的节律性则和丘脑相关，含有丰富的大脑活动信息。通常我们所接触的脑电图都是头皮脑电图，在有些特殊场合还需要皮下部位的脑电图，脑电信号主要有以下几个特点：

（1）脑电信号只有50pV左右，所以非常的微弱，通常头皮脑电信号，超过100pV的可以认作是噪声。脑电信号按照波幅值可以分为高、中、低三种:低波幅值小于25pV；中波幅值大于25pV小于50pV；高波幅值大于50pV。

（2）具有随机性及非平稳性。脑电信号被影响的因素很多，但规律通常都没有被识别，通常来说，脑电信号的规律从大量的数据统计、大量的技术处理检测、识别和估计结果中显示，并且生命体对外界的自适应力，以及生理因素的作用都对脑电信号产生了影响，所以脑电信号具有着随机性和非平稳性，并且一直随着时间在变化。

（3）具有非高斯、非线性的特征。生物组织自适应和生理机使得人体脑电的信号有非线性的特性，当前信号处理通常通过线性系统分析基础上进行，所以在分析方法上如何最小地去减小非线性误差在脑电信号的处理上也应该要考虑。

（4）脑电信号容易受到诸多的背景噪声干扰。影响脑电波的因素还有很多。比如人的年龄，当人在50岁以后，慢波又可以逐渐回升，还有着不同程度的基频慢波。脑波还更易受到意识、情绪以及思维状态等因素的影响。

脑电波在病理的状态下的形态也经常会出现一些异常瞬态波。尖波周期范围是在80~200ms，其波形快速上升、缓慢下降，类似于三角波，病症常见于癫痫。棘波多见于局限性的癫痫，而棘慢综合波是通过棘波和慢波所构成的复合波。

鉴于此，本项目采用谱分析方法，对两个来源（PhysioNet数据库和自测数据库）的脑电信号进行了研究，目标是应用不同的时频谱分析技术评估相应的结果。算法程序运行环境为MATLAB R2021b，执行EEG信号的谱分析，也可迁移至金融时间序列，地震信号，机械振动信号，语音信号，声信号等一维时间序列信号。

部分代码如下：

%EEG Signal Spectral Analysis
%Load data & Initialize params
%Sleep dataset
clear;
[x, Fs, Start_date, Start_time, Label, Dimension, Coef, Nmb_chans,N] = readedf_EX1('sc4002e0.rec',0,0,360);
windows = int16([128 256 512]);
overlaps = double([0 0.25 0.50 0.75]);
dft_points = [64 128 256 512 1024];
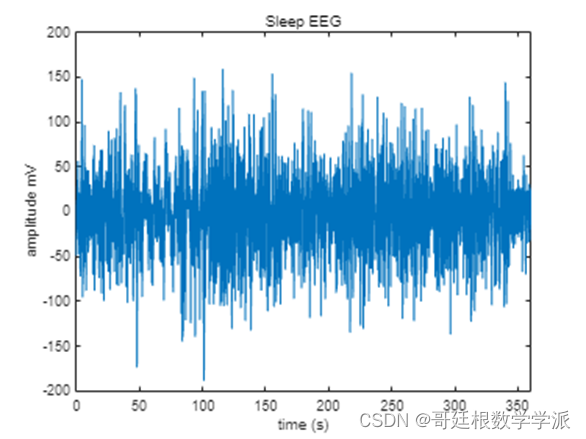
Signal overview
figure
time = linspace(0,length(x)/Fs, length(x));
plot(time,x)
axis('normal')
title('Sleep EEG')
xlim([0 length(time)/Fs])
xlabel('time (s)')
ylabel('amplitude mV')1. PSD params experiment1.1 Window size
figure
hold on
for i=1:length(windows)[pxx, f] = pwelch(x,windows(i),overlaps(3)*windows(i),dft_points(i),100);plot(f, pow2db(pxx))
end
legend(sprintf('w=%d', windows(1)), ...sprintf('w=%d',windows(2)), ...sprintf('w=%d', windows(3)))
xlabel('')
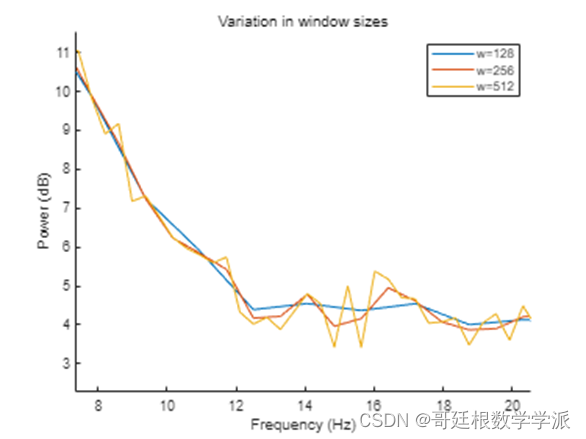
title('Variation in window sizes')
xlabel('Frequency (Hz)')
ylabel('Power (dB)')
hold off
% Better visualization for comparision
xlim([7.37 20.53])
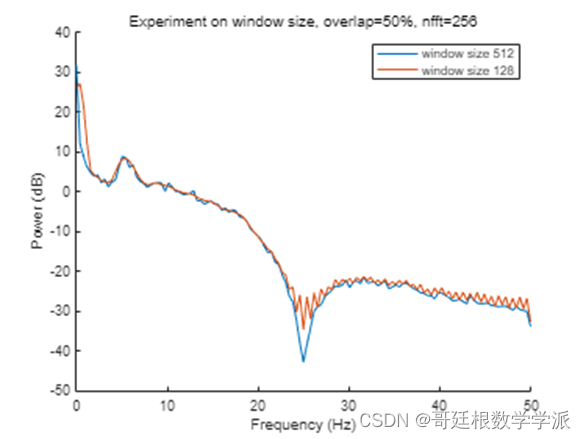
ylim([2.30 11.52])1.2 Overlap
figure
hold on
noverlaps = overlaps .* 128;
for i=1:length(noverlaps)[pxx, f] = pwelch(x, windows(1), noverlaps(floor(i)), dft_points(1), 100);plot(f, pow2db(pxx),'LineWidth',1)
end
legend(sprintf('overlap=%d %', overlaps(1)*100), ...sprintf('overlap=%d %', overlaps(2)*100), ...sprintf('overlap=%d %', overlaps(3)*100),...sprintf('overlap=%d %', overlaps(4)*100))
xlabel('')
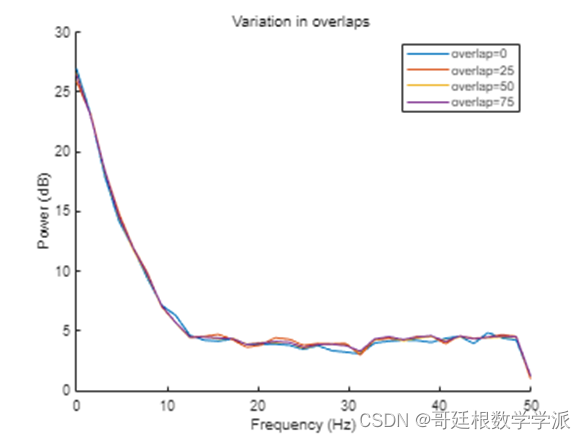
title('Variation in overlaps ')
xlabel('Frequency (Hz)')
ylabel('Power (dB)')
hold off1.3 Number of DFT points
figure
hold on
for i=1:length(dft_points)[pxx, f] = pwelch(x,windows(1),overlaps(2)*windows(1),dft_points(i),100);plot(f, pow2db(pxx))
end
legend(sprintf('nfft=%d', dft_points(1)), ...sprintf('nfft=%d',dft_points(2)), ...sprintf('nfft=%d',dft_points(3)), ...sprintf('nfft=%d',dft_points(4)), ...sprintf('nfft=%d', dft_points(5)))
xlabel('')
title('Variation in number of DFT points')
xlabel('Frequency (Hz)')
ylabel('Power (dB)')
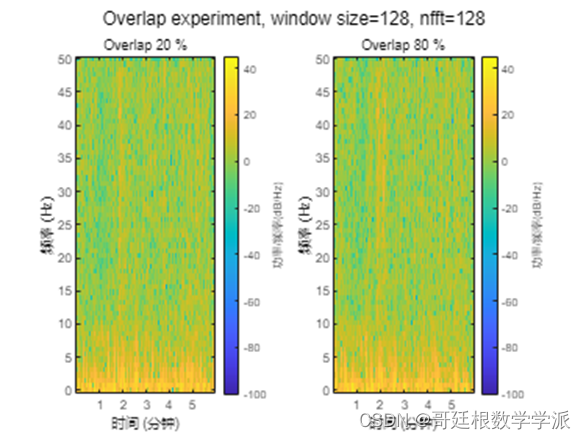
hold off2. Spectrogram params experimentspec_w_1 = 128;
spec_w_2 = 512;
spec_o_1 = 0.5;
spec_o_2 = 0.8;
spec_o_3 = 0.2;
spec_nfft_1 = 128;
spec_nfft_2 = 1024;2.1 Window size
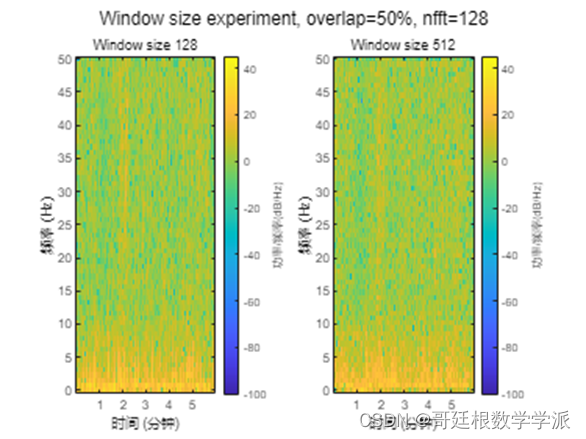
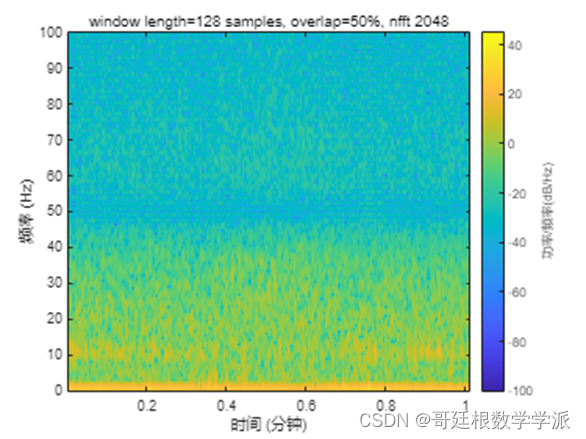
Small window size results in high detail frequecy representation.
Large window size results in blocky-looking frequecy representation.
figure;
subplot(1,2,1);
spectrogram(x,spec_w_1,64,128,Fs,'yaxis');
set(gca, 'Clim', [-100 45]);
title(sprintf('Window size %d', spec_w_1))subplot(1,2,2);
spectrogram(x,spec_w_2, spec_o_1 * spec_w_2,128,Fs,'yaxis');
set(gca, 'Clim', [-100 45]);
title(sprintf('Window size %d', spec_w_2))sgtitle(sprintf('Window size experiment, overlap=%d%%, nfft=%d', spec_o_1*100, spec_nfft_1));

出图如下：