一遍过。

当前房屋偷与不偷取决于 前一个房屋和前两个房屋是否被偷了。所以这里就更感觉到，当前状态和前面状态会有一种依赖关系，那么这种依赖关系都是动规的递推公式。

class Solution {
public:int rob(vector<int>& nums) {vector<vector<int>> dp(40001,vector<int>(2,0));for(int i=1;i<=nums.size();i++){int tmp=max(dp[i-1][0],dp[i-1][1]);dp[i][0]=max(tmp,dp[i][0]);dp[i][1]=max(dp[i-1][0]+nums[i-1],dp[i][1]);}return max(dp[nums.size()][0],dp[nums.size()][1]);}
};

 题解的递推公示少了一个维度，

决定dp[i]的因素就是第i房间偷还是不偷。

如果偷第i房间，那么dp[i] = dp[i - 2] + nums[i] ，即：第i-1房一定是不考虑的，找出 下标i-2（包括i-2）以内的房屋，最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。

如果不偷第i房间，那么dp[i] = dp[i - 1]，即考 虑i-1房，（注意这里是考虑，并不是一定要偷i-1房，这是很多同学容易混淆的点）

然后dp[i]取最大值，即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);

class Solution {
public:int rob(vector<int>& nums) {if (nums.size() == 0) return 0;if (nums.size() == 1) return nums[0];vector<int> dp(nums.size());dp[0] = nums[0];dp[1] = max(nums[0], nums[1]);for (int i = 2; i < nums.size(); i++) {dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);}return dp[nums.size() - 1];}
};

 

首尾元素大概知道要分为是否考虑末尾元素，考虑了末尾元素的情况对应选取第二个到最后一个元素，没有题解方法清晰。看了题解。

 可以分为三种情况，

• 情况一：考虑不包含首尾元素；
• 情况二：考虑包含首元素，不包含尾元素；
• 情况二：考虑包含首元素，不包含尾元素；（其实情况二和情况三包括了情况一）

class Solution {
public:int rob(vector<int>& nums) {if(nums.size()==0) return 0;if(nums.size()==1) return nums[0];if(nums.size()==2) return max(nums[0],nums[1]);return max(robrange(nums,0,nums.size()-2),robrange(nums,1,nums.size()-1));}int robrange(vector<int>& nums,int start,int end){if(start==end) return nums[end];vector<int> dp(nums.size()+1,0);dp[start]=nums[start];dp[start+1]=max(nums[start],nums[start+1]);for(int i=start+2;i<=end;i++){dp[i]=max(dp[i-2]+nums[i],dp[i-1]);}return dp[end];}
};

 

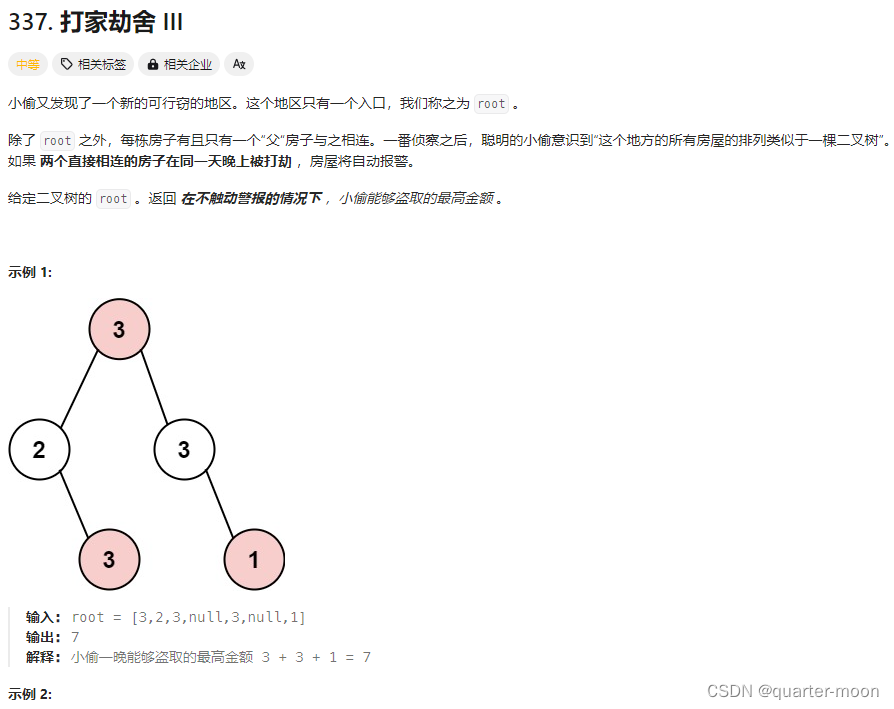
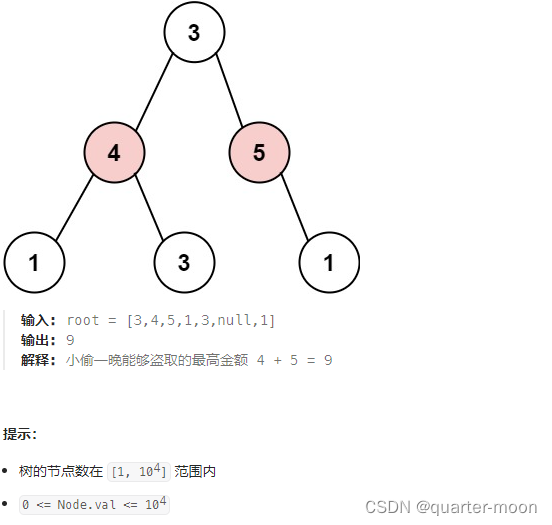
 我一开始写的递归版本，超出时间限制了。原因是在算左边的孩子节点时，和算他的左右孩子节点会重复（各自会递归算一次）。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int rob(TreeNode* root) {int tmpl=0,tmpr=0 ;int tmpll=0,tmplr=0,tmprl=0,tmprr=0;if(root->left){tmpl=rob(root->left);if(root->left->left){tmpll=rob(root->left->left);}if(root->left->right){tmplr=rob(root->left->right);}}if(root->right){tmpr=rob(root->right);if(root->right->left){tmprl=rob(root->right->left);}if(root->right->right){tmprr=rob(root->right->right);}}return max(root->val+tmpll+tmplr+tmprl+tmprr,tmpl+tmpr);}
};

看了题解：对于树的话，首先就要想到遍历方式，前中后序（深度优先搜索）还是层序遍历（广度优先搜索）。本题一定是要后序遍历，因为通过递归函数的返回值来做下一步计算。

要注意特判断

if (root == NULL) return 0;
if (root->left == NULL && root->right == NULL) return root->val;

 记忆化搜索：要会使用unordered_map

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:unordered_map<TreeNode*, int> mp;int rob(TreeNode* root) {if(root==NULL) return 0;if(root->left==NULL&&root->right==NULL) return root->val;int tmpl=0,tmpr=0 ;int tmpll=0,tmplr=0,tmprl=0,tmprr=0;if(mp[root]) return mp[root];if(root->left){tmpl=rob(root->left);mp[root->left]=tmpl;if(root->left->left){tmpll=rob(root->left->left);mp[root->left->left]=tmpll;}if(root->left->right){tmplr=rob(root->left->right);mp[root->left->right]=tmplr;}}if(root->right){tmpr=rob(root->right);mp[root->right]=tmpr;if(root->right->left){tmprl=rob(root->right->left);mp[root->right->left]=tmprl;}if(root->right->right){tmprr=rob(root->right->right);mp[root->right->right]=tmprr;}}return max(root->val+tmpll+tmplr+tmprl+tmprr,tmpl+tmpr);}
};

动态规划方法：

 对当前节点是偷与不偷两种状态：dp数组（dp table）以及下标的含义：下标为0记录不偷该节点所得到的的最大金钱，下标为1记录偷该节点所得到的的最大金钱。

如果是偷当前节点，那么左右孩子就不能偷，val1 = cur->val + left[0] + right[0]; （如果对下标含义不理解就再回顾一下dp数组的含义）

如果不偷当前节点，那么左右孩子就可以偷，至于到底偷不偷一定是选一个最大的，所以：val2 = max(left[0], left[1]) + max(right[0], right[1]);

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:int rob(TreeNode* root) {vector<int> res=robrange(root);return max(res[0],res[1]);}vector<int> robrange(TreeNode* root){if(root==NULL) return vector<int>{0,0};vector<int> left=robrange(root->left);vector<int> right=robrange(root->right);return vector<int>{max(left[0],left[1])+max(right[0],right[1]),root->val+left[0]+right[0]};}
};

上题是树形dp入门。