目录

1.什么是二叉搜索树

2.二叉搜索树的查找

3.二叉搜索树插入

4.二叉搜索树的删除

1.删除的节点只有左子树或者右子树

2.删除节点左右子树都有的情况

5.代码

---

1.什么是二叉搜索树

左节点的值小于根节点

右节点大于根节点

左右子树也满足上面两个条件

例：arr[] = {5,2,1,3,4,7,6,8} 转化为二叉搜索树

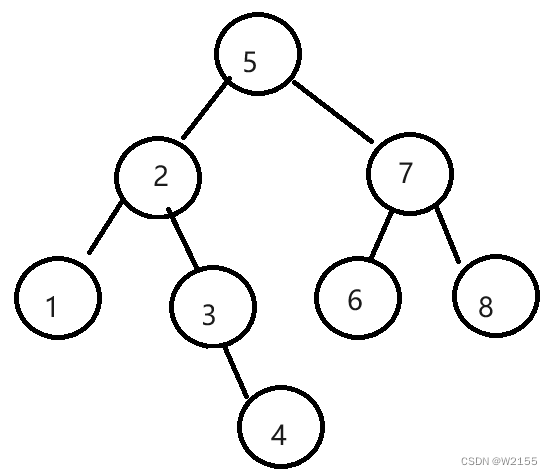
2.二叉搜索树的查找

思路：寻找4，4比5小去左子树寻找-> 4比2大去右子树寻找->4比3大去右子树寻找->找到4。

3.二叉搜索树插入

思路：查找插入元素可以存储的位置 ，插入。

例：插入9, 9比5大去右子树寻找->9比7大去右子树寻找->9比8大去右子树寻找->找到9可以插入的位置->将9插入8的右子树。

4.二叉搜索树的删除

二叉搜索树删除的情况可以分成两种

1.删除的节点只有左子树或者右子树

 如果删除节点是删除节点父亲节点的左子树，那就把删除节点的左子树或者右子树，托付给父亲节点的左子树。

 如果删除节点是删除节点父亲节点的右子树，那就把删除节点的左子树或者右子树，托付给父亲节点的右子树。

例：删除3就把4托付给2的右子树

       删除4就把空节点托付给3的右子树

2.删除节点左右子树都有的情况

找左子树的最右节点或者右子树的最左节点替换删除节点，再将左子树最右节点或者右子树最左节点删除，因为最右节点一定没有右子树，最左节点一定没有左子树，就把问题转化为情况1了。

例：删除2

用右子树的最左节点：3为右子树最左节点，把3赋值给2，去右子树把3删除，把4托付给3的右子树 。

用左子树的最右节点：1为左子树最右节点，把1赋值给2，去左子树把1删除，把空节点托付给1的左子树。

5.代码

#pragma oncenamespace V
{template<class K>struct BinarySearchTreeNode//节点{typedef struct BinarySearchTreeNode<K> Node;BinarySearchTreeNode():_val(){}BinarySearchTreeNode(const K& val):_val(val){}Node* _left = nullptr;Node* _right = nullptr;K _val;};template <class K>class BST//二叉搜索树{typedef struct BinarySearchTreeNode<K> Node;public:BST()//构造函数:_root(nullptr){}BST(const BST<K> &t){_root = Copy(t._root);}Node* Copy(Node* root){if (nullptr == root){return nullptr;}Node* newNode = new Node(root->_val);newNode->_left = Copy(root->_left);newNode->_right = Copy(root->_right);return newNode;}BST<K>& operator=(BST<K> t){std::swap(_root,t._root);return *this;}bool Insert(const K& key){if (nullptr == _root){_root = new Node(key);return true;}Node* cur = _root;Node* parent = nullptr;while (nullptr != cur){if (key > cur->_val){parent = cur;cur = cur->_right;}else if (key < cur->_val){parent = cur;cur = cur->_left;}else { return  false; }}Node* newNode = new Node(key);if (parent->_val > newNode->_val){parent->_left = newNode;return true;}else{parent->_right = newNode;return true;}}Node* Find(const K& key){Node* cur = _root;while (nullptr != cur){if (cur->_val > key){cur = cur->_left;}else if (cur->_val < key){cur = cur->_right;}else if (cur->_val == key){return cur;}}return nullptr;}bool Erase(const K& key){Node* cur = _root;Node* parent = _root;while (nullptr != cur){if (cur->_val > key){parent = cur;cur = cur->_left;}else if (cur->_val < key){parent = cur;cur = cur->_right;}else if (cur->_val == key)//找到key{if (nullptr == cur->_left)//当key左子树为空{if (_root == cur){_root = cur->_right;}else if (cur == parent->_left)//当cur是父亲的左子树{parent->_left = cur->_right;}else if(cur == parent->_right)//cur是父亲的右子树{parent->_right = cur->_right;}delete cur;cur = nullptr;return true;}else if (nullptr == cur->_right)//key的右子树为空{if(cur == _root){ _root = cur->_left;}else if (cur == parent->_left){parent->_left = cur->_left;}else{parent->_right = cur->_left;}delete cur;cur = nullptr;return true;}else //左右子树都不为空 {Node* LNode = cur->_left;Node* LParent = cur;while (LNode->_right)//找左子树的最右节点 替换cur {LParent = LNode;LNode = LNode->_right;}cur->_val = LNode->_val;//修改值//最右节点没有右子树if (LNode == LParent->_left){LParent->_left = LNode->_left;}else{LParent->_right = LNode->_left;}delete LNode;LNode = nullptr;return true;}}}return false;}void InOrder(){return _InOrder(_root);}void Destory(){_Destory(_root);}~BST(){Destory();}///递归实现bool FindR(const K &val){return _FindR(_root,val);}bool InsertR(const K& val){return _InsertR(_root,val);}bool EraseR(const K& val){return _EraseR(_root, val);}private:Node* _root;void _InOrder(Node* root){if (nullptr == root){return;}std::cout << root->_val << " ";_InOrder(root->_left);_InOrder(root->_right);}void _Destory(Node * root){if (nullptr == root){return;}_Destory(root->_left);_Destory(root->_right);delete root;}bool _InsertR(Node * &root, const K &val){if (nullptr == root){root = new Node(val);return true;}if (root->_val > val)_InsertR(root->_left, val);else if (root->_val < val)_InsertR(root->_right, val);return false;}bool _FindR(Node * root,const K&val){if (nullptr == root)return false;if (root->_val > val)_FindR(root->_left, val);else if (root->_val < val)_FindR(root->_right, val);else return true;}bool _EraseR(Node * &root,const K&val){if (root == nullptr){return false;}if(root->_val > val){_EraseR(root->_left,val);}else if (root->_val < val){_EraseR(root->_right, val);}else{Node* del = root;//当左孩子为空，if (nullptr == root->_left){root = root->_right;}else if (nullptr == root->_right){root = root->_left;}else {Node* leftmax = root->_left;while (leftmax->_right)//左子树的最右节点{leftmax = leftmax->_right;}swap(leftmax->_val, root->_val);return _EraseR(root->_left,val);}delete del;return true;}}};}