
刷题
- 1022.从根到叶的二进制数之和
- 题目描述:
- 思路一(dfs深搜万能版)
- 思路二 (栈迭代巧解版)
- 总结
- Thanks♪(・ω・)ノ谢谢阅读!!!
- 下一篇文章见!!!
1022.从根到叶的二进制数之和
题目描述:

题目给出一棵二叉树,我们需要统计计算每条路径的二进制之和。给出的测试用例是
1,0,1,0,1,0,1
则运算为:(100) + (101) + (110) + (111) = 4 + 5 + 6 + 7 = 22。
难点就在于如何进行每个节点的储存计算,一般来说二叉树都会使用遍历或栈来进行运算。那就让我们来看看这个题如何完美解答吧!!!
思路一(dfs深搜万能版)
一般我们遇到二叉树都会想到遍历,但是这道题我们需要做到是如何记录该节点之前的数据,只有这样才能来进行每条路径的计算。所以首先我们需要单独写入一个函数来满足我们的需求
dfs(struct TreeNode* root ,int val)
其中root负责遍历,val来储存之前的数据,这样就可以进行操作了:
首先我们需要确定递归的返回条件,明确条思路才能顺畅解题!
- 如果二叉树为空 返回零
- 如果该节点为叶子节点 返回节点值与前面数据值 val 的和
- 如果不是叶子节点 返回左右二叉树的和 与 前面数据值 val 的和
确定了返回条件就简单了,把条件写好,剩下的交给计算机计算就OK了!!!
int dfs(struct TreeNode* root,int val){//如果二叉树为空 返回零if(root == NULL) return 0;//如果该节点为叶子节点 返回节点值与前面数据值 val 的和else if(!root->left&&!root->right) return (val << 1) | root->val;//相当于(val*2)+ root->val//如果不是叶子节点 返回左右二叉树的和与前面数据值 val 的和else{val = (val<<1) | root->val;//相当于(val*2)+ root->valreturn dfs(root->left,val) + dfs(root->right ,val);}
}
int sumRootToLeaf(struct TreeNode* root){return dfs(root,0);
}
这里之所以使用位操作而不是使用乘法操作,是因为使用位操作效率更高!乘法的底层是位运算乘法器,所以直接使用就避免了多余的操作。
来看运行结果:
直接秒天秒地秒世界!!!过啦!!!
思路二 (栈迭代巧解版)
该算法是使用栈来模拟函数递归的过程:
typedef struct TreeNode Node;int sumRootToLeaf(struct TreeNode* root){Node** stack = (Node*)malloc(sizeof(Node)*1001);Node* prev = NULL;int ret = 0;int val = 0,top = 0;while(root != NULL || top){while(root != NULL){stack[top++] = root;val = (val << 1)| root->val;root = root->left;}root = stack[top - 1];if(root->right == NULL || root->right == prev){if(root->right == NULL && root->left == NULL){ret += val;}val >>= 1;top--;prev = root;root = NULL;}else{root = root->right;}}free(stack);return ret;
}
选择遍历二叉树的办法是:
- 先创建一个指针 prev 用于储存上一个读取的节点
- 先在栈里储存二叉树左边的一条路径(一直 root = root->left)压栈
- 然后取出栈顶节点(root = stack[top-1])
接下来是非常关键的一步:
4. 如果该节点的右节点为空 或者 右节点已经遍历过了 就跳过 更替指针(prev = root;root = NULL)否则就进入root 右半树(root = root->right)
5. 循环执行2 - 4 就可以实现效果
只看代码还是十分难理解的,我使用图来简单解释一下:
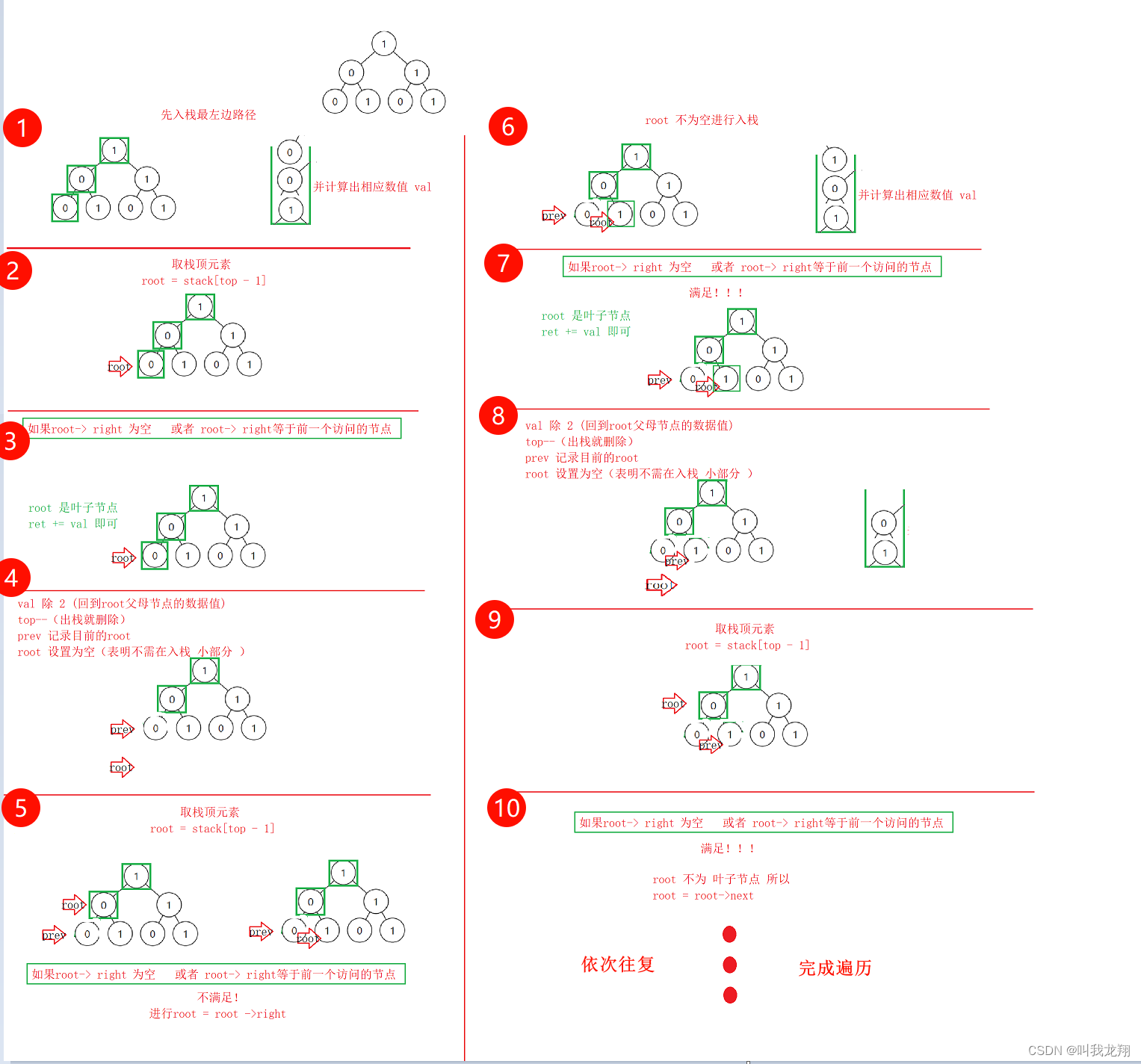
就这样,一步一步进行就可以遍历整个树,是不是十分巧妙。结果自然是过啦!!!!
这种方法比较复杂,是非递归遍历二叉树的常用方法。
总结
通过这道题,我学会了递归的深度搜索方法,快速解决问题
也初步认识到了非递归遍历二叉树的方法。但还是不太理解,不知道是如何推出来的。

)














——网络通信入门基本概念)


