3. Residual Denoising Diffusion Models

   该文提出一种残差去噪扩散模型（RDDM）可用去图像生成和图像修复（如去除阴影、去雨、暗光提升等）。该文最大的特点是提出一种双扩散模型，在扩散过程中不仅包含噪声$ϵ$扩散，还包含残差信息$I_{res}$的扩散，这里的残差信息就是退化图像$I_{in}$和$I_0$之间的差值。例如去雨任务中，带有雨的图像就是$I_{in}$，去雨之后的图像就是$I_0$。

  RDDM的扩散和重建过程如上图所示，如果$I_{in}$为0，RDDM就变成了正常的图像生成；如果$I_{in}$是退化的图像，RDDM就可以实现图像修复任务。扩散过程中带有噪声的退化图像$I_t$的计算方法如下所示$$I_t=I_{t-1}+I_{res}^t,I_{res}^t\backsim \mathcal{N}({\alpha }_t{I}_{res},{\beta }_t^{2}I)$$或者$$I_t=I_0+{\bar{\alpha }}_t{I}_{res}+{\bar{\beta }}_tϵ$$其中${\bar{\alpha }}_t={\sum }_{i=1}^t{\alpha }_i$，${\bar{\beta }}_t=\sqrt{{\sum }_{i=1}^t{\beta }_i^2}$。在扩散过程中，需要同时训练两个模型$I_{res}^{\theta }(I_t,t,I_{in})$和${ϵ}_{\theta }(I_t,t,I_{in})$分别来预测残差$I_{res}^{\theta }$和噪声${ϵ}_{\theta }$。模型训练的目标函数分别为$$L_{\text{res }}(\theta ):=\mathbb{E}\left[{\lambda }_{\text{res }}{\Vert I_{\text{res }}-I_{\text{res }}^{\theta }\left(I_t,t,I_{\text{in }}\right)\Vert }^2\right],L_{ϵ}(\theta ):=\mathbb{E}\left[{\lambda }_{ϵ}{\Vert ϵ-{ϵ}_{\theta }\left(I_t,t,I_{\text{in }}\right)\Vert }^2\right]$$
   在重建过程中，利用训练好的网络预测得到的残差$I_{res}^{\theta }$和噪声${ϵ}_{\theta }$就可以从$I_t$中恢复$I_{t-1}$，如下式$$I_{t-1}=I_t-\left({\bar{\alpha }}_t-{\bar{\alpha }}_{t-1}\right)I_{res}^{\theta }-\left({\bar{\beta }}_t-\sqrt{{\bar{\beta }}_{t-1}^2-{\sigma }_t^2}\right){ϵ}_{\theta }+{\sigma }_t{ϵ}_t\text{, where }{ϵ}_t\sim \mathcal{N}(0,\mathbf{I})$$其中${\sigma }_t^2=\eta {\beta }_t^2{\bar{\beta }}_{t-1}^2/{\bar{\beta }}_t^2$。
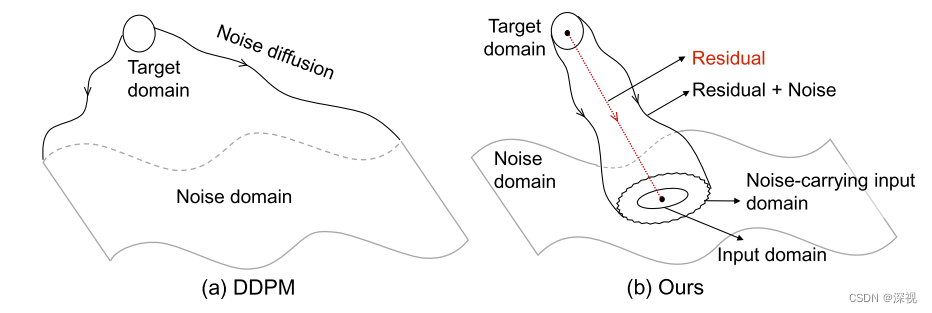
   作者提到扩散过程中，${\alpha }_t$控制着残差扩散的速度，${\beta }_t^2$控制着噪声扩散的速度，并且二者之间是彼此独立的，也就是说噪声扩散和残差扩散两个过程是可以解耦的。这样带来一个好处，就是可以更加精细的设计${\alpha }_t$和${\beta }_t^2$的取值和计算方式。作者提到残差扩散过程表示了从目标图像$I_0$到退化图像$I_{in}$之间的扩散方向，因此其更加注重的是确定性。而噪声扩散表示扩散过程中的随机干扰，其更加强调多样性。RDDM与DDPM之间的差异如下图所示， 残差信息的引入，就在最终的扩散得到的噪声中限定了一个范围，而不是完全不可知的一个随机分布。

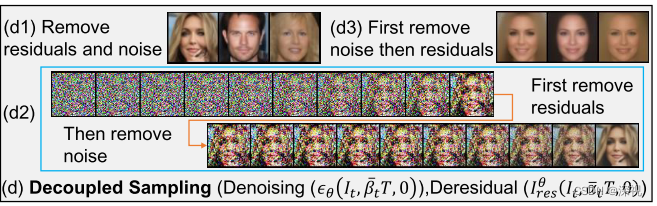
  作者后面用了很大篇幅去论证了在生成过程中，去噪和去除残差的过程是部分上路径独立的。如果先去除噪声后去除残差，生成结果就失去多样性；如果先去除残差，再去除噪声，则能够控制语义的变换。