以下是个人理解,希望进行讨论求解。
练习
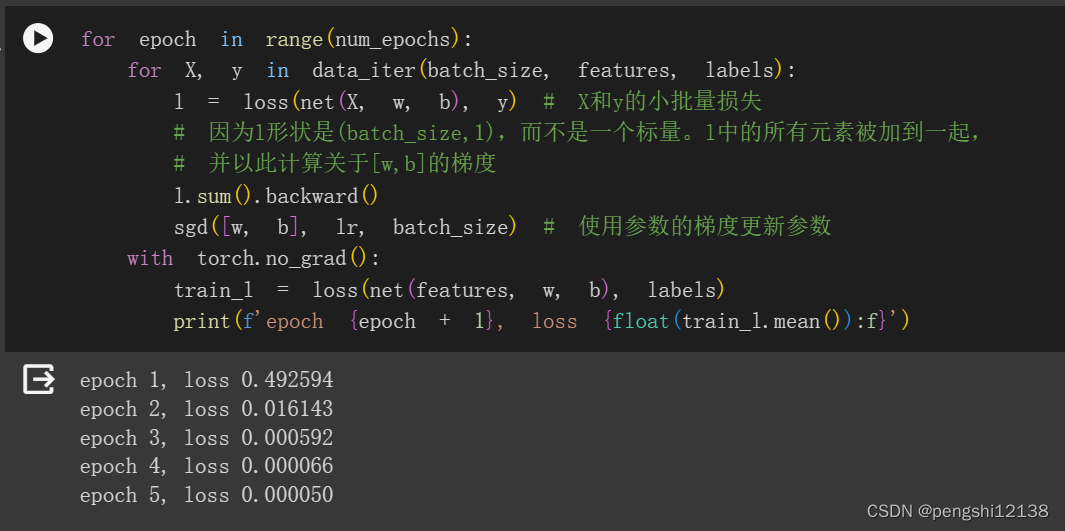
1. 如果我们将权重初始化为零,会发生什么。算法仍然有效吗?
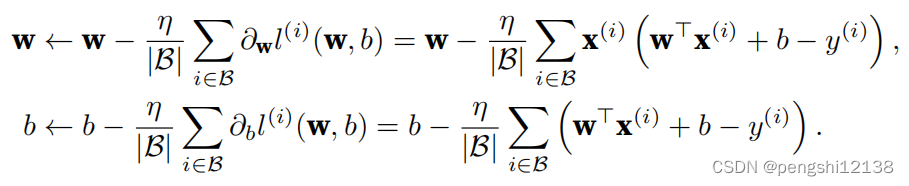
根据SGD算法公式如上,第一次迭代的值可知w只与b相关,而对于b的迭代更新,只是与b的初始值相关,x没有参与迭代的计算过程中,不能够达到收敛的目的。
进行运行可以如下结果:

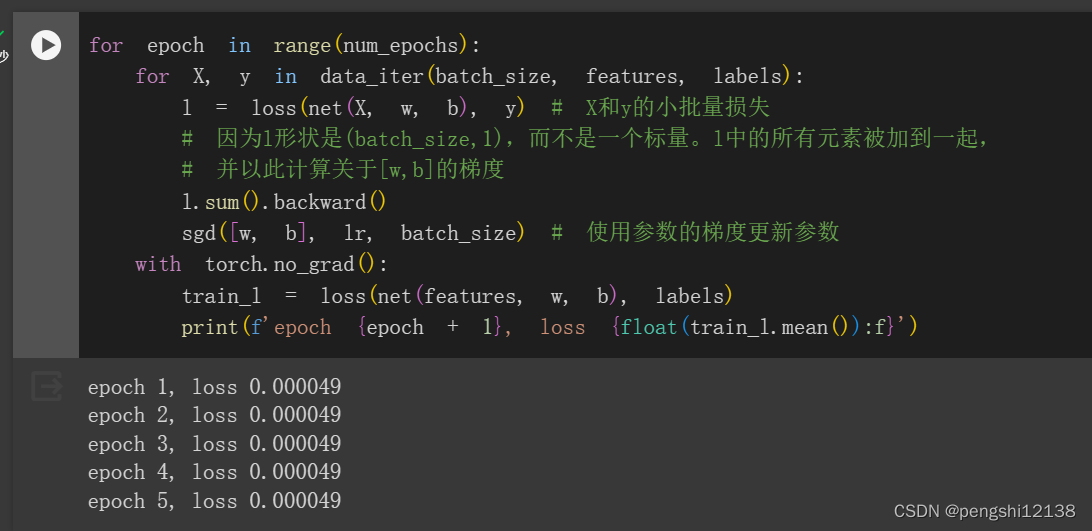
2. 假设试图为电压和电流的关系建立一个模型。自动微分可以用来学习模型的参数吗?
显而易见可行,因为 UR=I,I和U的关系是线性关系。
3. 能基于普朗克定律使用光谱能量密度来确定物体的温度吗?
能基于普朗克定律使用光谱能量密度如下:
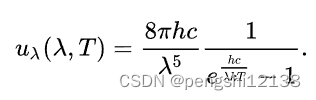
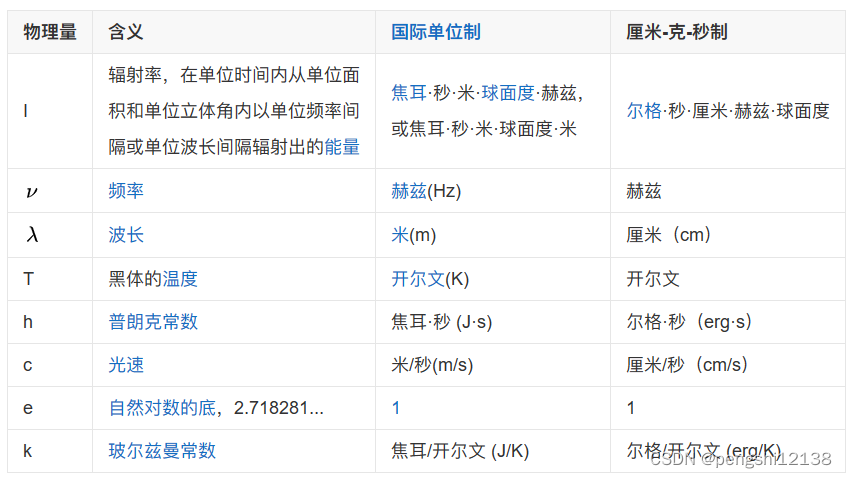
推导公式最后如下,可得其u与T之间是线性关系,是正比情况,所以可以利用SGD的方法通过数据进行拟合。
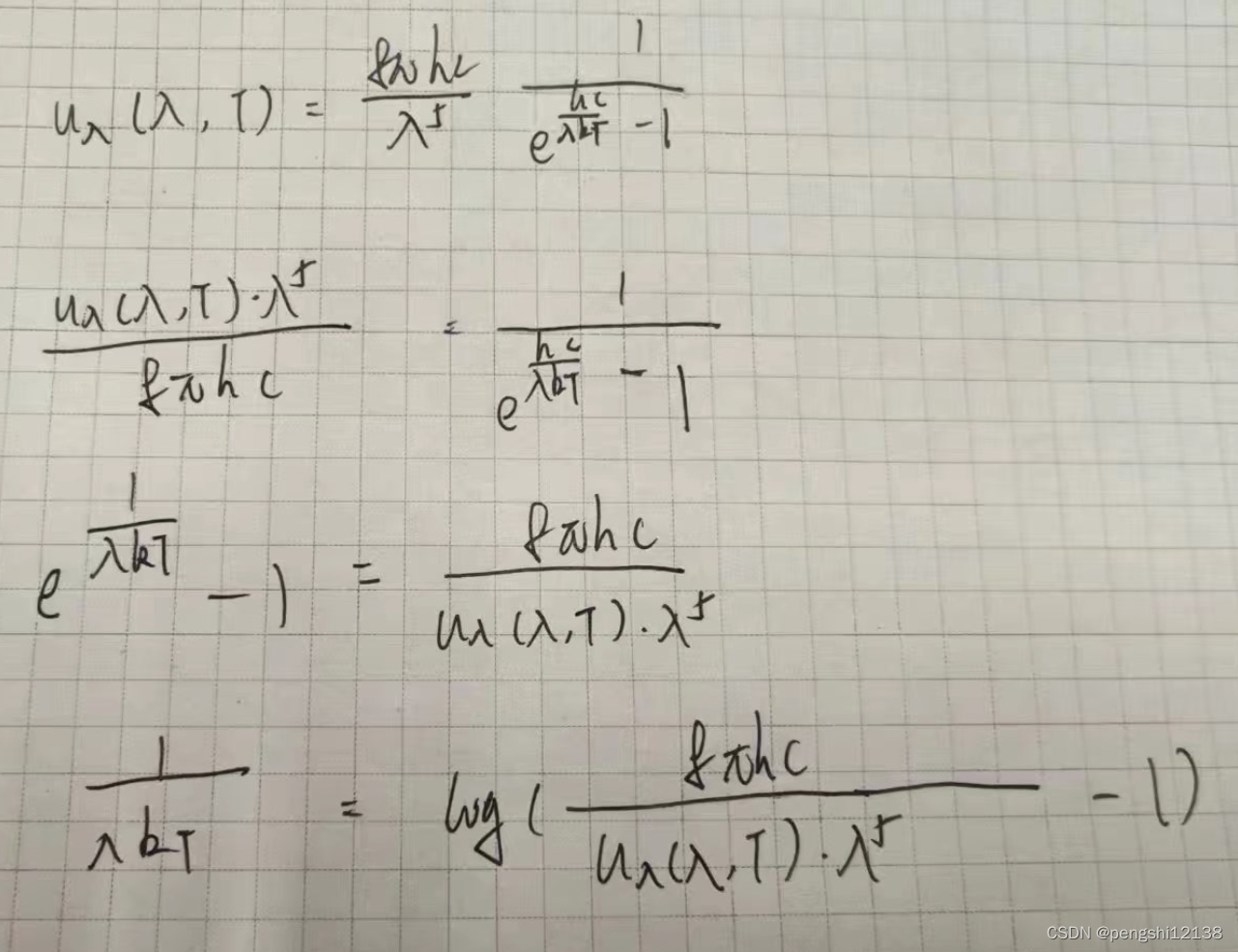
4. 计算二阶导数时可能会遇到什么问题?这些问题可以如何解决?
显而易见存在一阶导数光滑,但是二阶导数曲线不光滑的情况,类似于一阶导数驻点突变问题。利用阈值判断停止计算,或者调整学习率等,参考上一章的答案。以上是我能够想到的问题。显然不是足够,所以动用一下gpt帮忙:

5. 为什么在squared_loss函数中需要使用reshape函数?
要将真实值y的形状转换为和预测值y_hat的形状相同。根据函数矩阵计算可知,x是102大小,w是21,得出的y_hat是101,但是y是110,所以需要转置。
6. 尝试使用不同的学习率,观察损失函数值下降的快慢。
学习率0.01的时候
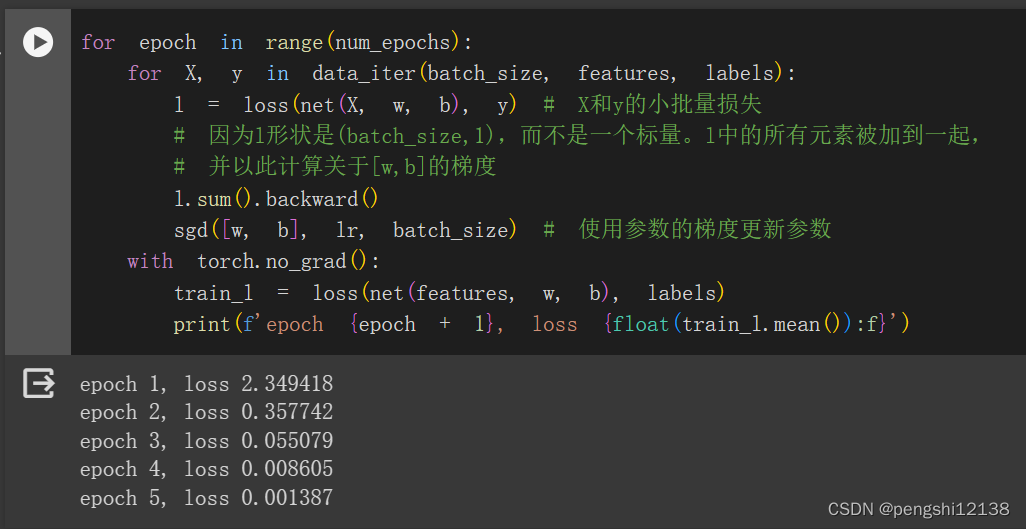
学习率0.02的时候
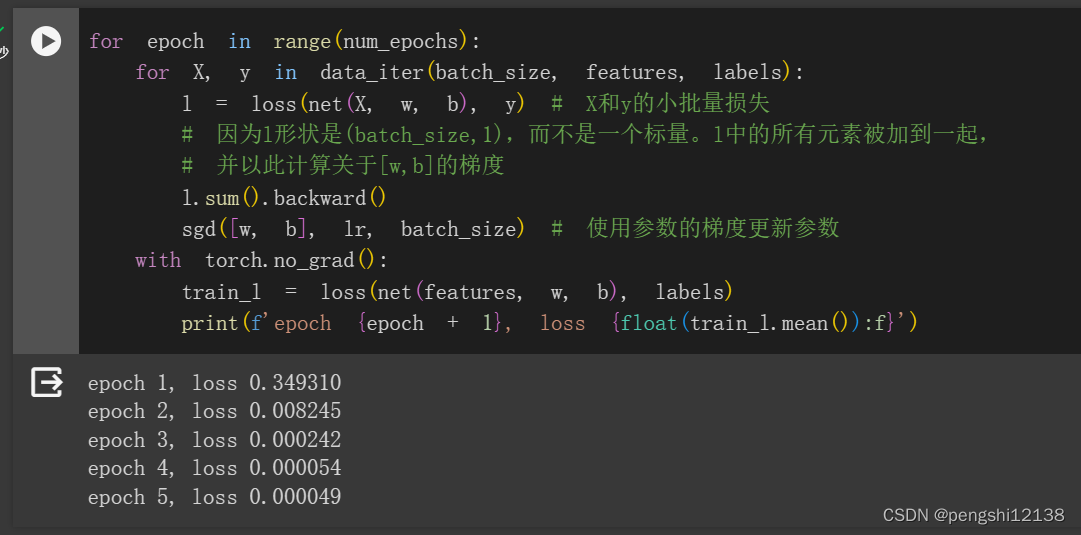
可知道收敛速度不同,收敛精度不同
7. 如果样本个数不能被批量大小整除,data_iter函数的行为会有什么变化?
修改代码batch_size设置为11,进行运行,发现可运行,说明了最后一个batch直接被运算抛弃了,不参与计算。
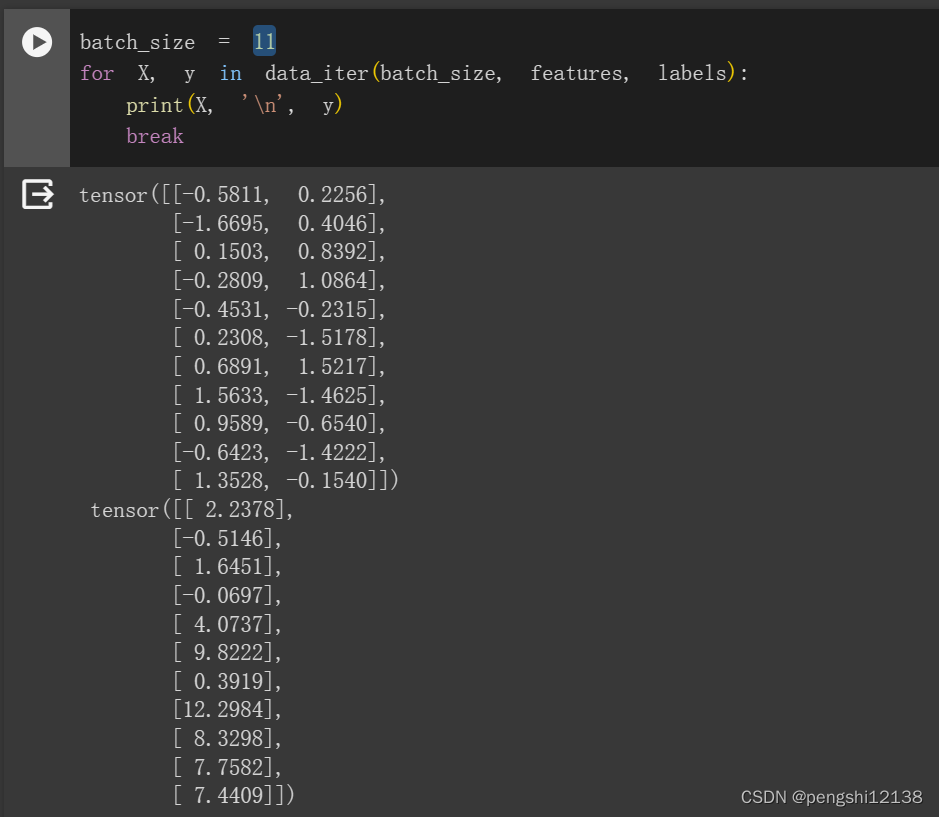









,匈牙利算法(二分图的最大匹配) //概念,应用场景,判定证明,算法思路,示例)






)


