338.比特位计数
给你一个整数 n ,对于 0 <= i <= n 中的每个 i ,计算其二进制表示中 1 的个数 ,返回一个长度为 n + 1 的数组 ans 作为答案。
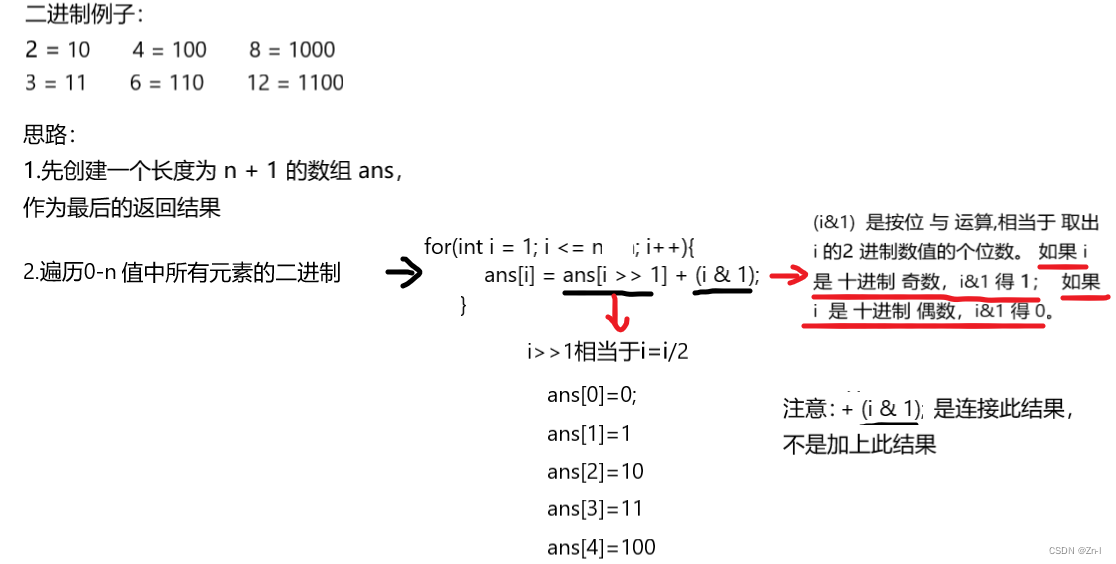
class Solution {public int[] countBits(int n) {/** 思路:* 1.创建一个长度为 n + 1 的数组 ans 作为返回结果* 2.遍历0-num值中所有元素的二进制值,并将其计算结果存在数组中去* ★i>>1相当于i=i/2;i&1 按位与运算,当i为十进制奇数时,返回结果为1;反之,结果为0*/int ans[] = new int[n + 1];for (int i = 0; i <= n; i++) {ans[i] = ans[i >> 1] + (i & 1);}return ans;}
}
1025.除数博弈
爱丽丝和鲍勃一起玩游戏,他们轮流行动。爱丽丝先手开局。
最初,黑板上有一个数字 n 。在每个玩家的回合,玩家需要执行以下操作:
- 选出任一
x,满足0 < x < n且n % x == 0。 - 用
n - x替换黑板上的数字n。
如果玩家无法执行这些操作,就会输掉游戏。
只有在爱丽丝在游戏中取得胜利时才返回 true 。假设两个玩家都以最佳状态参与游戏。
示例 1:
输入:n = 2 输出:true 解释:爱丽丝选择 1,鲍勃无法进行操作。
示例 2:
输入:n = 3 输出:false 解释:爱丽丝选择 1,鲍勃也选择 1,然后爱丽丝无法进行操作。
动态规划法:
思路:由题可知,当到爱莎选择时,n若为偶数,则爱莎获胜;反之,鲍勃获胜
* 可先判断:n==1 ---> 鲍勃获胜
* n==2 ---> 爱莎获胜
* Alice 在 n的位置能不能胜利,取决于 n−x的位置 Bob能不能胜利。 即bl[i-j]若为false,则爱莎可获胜
* 若 n−x这个位置 Bob无法胜利,则 Alice在位置 n一定是能胜利的,即 dp[n] = true,此时直接结束内层循环即可。
class Solution {public boolean divisorGame(int n) {if (n == 1)return false;if (n == 2)return true;// 创建boolean数组boolean[] bl = new boolean[n + 1];bl[1] = false;bl[2] = true;for (int i = 3; i <= n; i++) {bl[i] = false; //先对bl[i]赋值// 题目:选出任一 x(j),满足 0 < x (j)< n(i) 且 n % x == 0for (int j = 1; j < i; j++) {if (i % j == 0 && !bl[i - j]) {bl[i] = true;break;}}}return bl[n];}
}数学法:
思路:因为爱丽丝先手开局,当到爱莎选择时,n若为偶数,则爱莎获胜;反之,鲍勃获胜,因此可判断n是否为偶数
class Solution {public boolean divisorGame(int n) {return n % 2 == 0;}
}



















 路由传参的2种方法)