🍉CSDN小墨&晓末:https://blog.csdn.net/jd1813346972
个人介绍: 研一|统计学|干货分享
擅长Python、Matlab、R等主流编程软件
累计十余项国家级比赛奖项,参与研究经费10w、40w级横向
文章目录
- 1 目的
- 2 Holt-Winters三参数指数平滑乘法模型
- 3 Holt-Winters三参数指数平滑乘法模型预测
1 目的
该篇文章主要展示针对时序进行Holt-Winters建模,案例数据同 时间序列分析实战(三):时序因素分解法:某欧洲小镇1963年1月至1976年12月每月旅馆入住的房间数构成时间序列 x t x_t xt。
2 Holt-Winters三参数指数平滑乘法模型
通过上一篇 Blog 知道该时序数据具有季节效应,并且具有长期趋势,考虑首先建立Holt-Winters三参数指数平滑乘法模型:
x t = [ a ( t ) + b ( t ) ] c ( t ) x_t=[a(t)+b(t)]c(t) xt=[a(t)+b(t)]c(t)
运行程序:
fit1=HoltWinters(data1,seasonal = "mult")
fit1
运行结果:
## Holt-Winters exponential smoothing with trend and multiplicative seasonal component.
##
## Call:
## HoltWinters(x = data1, seasonal = "mult")
##
## Smoothing parameters:
## alpha: 0.01567674
## beta : 0.008068444
## gamma: 0.4392594
##
## Coefficients:
## [,1]
## a 875.5123349
## b 1.9568538
## s1 0.9301067
## s2 0.8613974
## s3 0.8741871
## s4 0.9798006
## s5 0.9624445
## s6 1.0964284
## s7 1.2846348
## s8 1.3110818
## s9 1.0004965
## s10 0.9987417
## s11 0.8628932
## s12 0.9793806
基于R最优拟合原则得到平滑系数 α \alpha α=0.01567674, β \beta β=0.008068444, γ \gamma γ=0.4392594。经迭代得到三个参数的最后迭代值: a ( t ) a(t) a(t)=875.5123349, b ( t ) b(t) b(t)=1.9568538,参数 c ( t ) c(t) c(t)的最后12个月估计值对应的是12个月的季节指数,见表1。
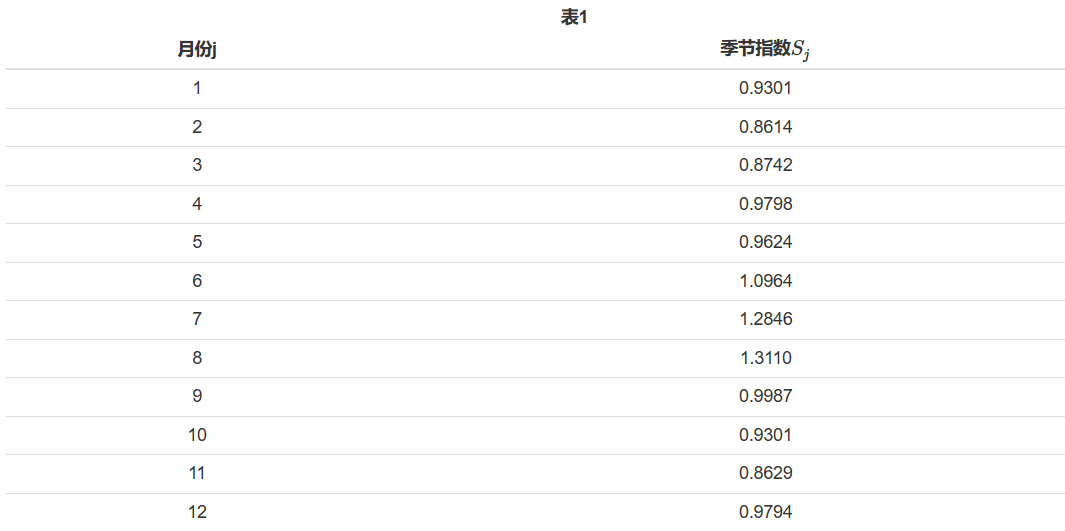
该序列向前任意 k k k期的预测值为:
x ^ t + k = ( 875.512 + 1.967 k ) S j , ∀ k ≥ 1 \hat x_{t+k}=(875.512+1.967k)S_j,\forall k≥1 x^t+k=(875.512+1.967k)Sj,∀k≥1
式中, j j j为 t + k t+k t+k期对应的季节。
3 Holt-Winters三参数指数平滑乘法模型预测
运行程序:
library(forecast)
fore1=forecast::forecast(fit1,h=36)
fore1$mean
运行结果:
## Jan Feb Mar Apr May Jun Jul
## 1977 816.1400 757.5353 770.4935 865.4968 852.0489 972.8099 1142.3105
## 1978 837.9810 777.7629 791.0214 888.5047 874.6492 998.5565 1172.4766
## 1979 859.8220 797.9904 811.5493 911.5126 897.2496 1024.3031 1202.6427
## Aug Sep Oct Nov Dec
## 1977 1168.3931 893.5675 893.9546 774.0477 880.4578
## 1978 1199.1802 917.0614 917.4073 794.3104 903.4559
## 1979 1229.9674 940.5553 940.8600 814.5731 926.4540
运行程序:
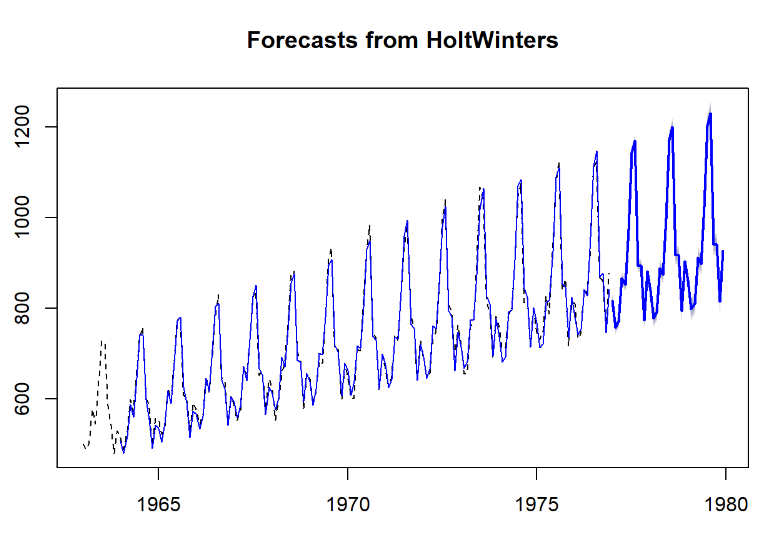
plot(fore1,lty=2,sub='图1 入住房间数序列Holt-Winters三参数指数平滑预测效果图')
lines(fore1$fitted,col=4)
运行结果:





![[算法沉淀记录] 排序算法 —— 堆排序](https://img-blog.csdnimg.cn/direct/69d12166b20b4e33807a075770a4e279.png)